Закон изменения и сохранения импульса системы тел

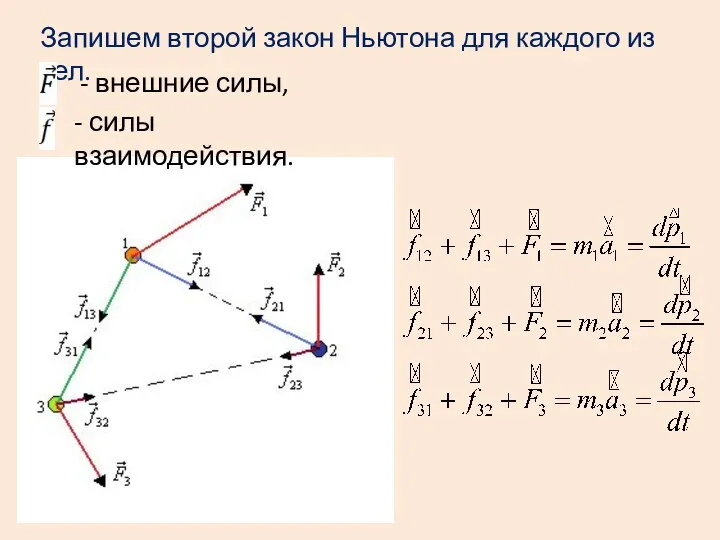
Запишем второй закон Ньютона для каждого из тел.
- внешние силы,
- силы взаимодействия.

Сумма внутренних сил равна нулю по третьему закону Ньютона, тогда
или
Сложим почленно все уравнения:

Закон изменения импульса системы тел:
равнодействующая внешних сил равна скорости изменения импульса системы.
- равнодействующая внешних сил;
- импульс системы тел.

Закон сохранения импульса:
в замкнутой системе тел векторная сумма импульсов тел, входящих в систему, есть величина постоянная.

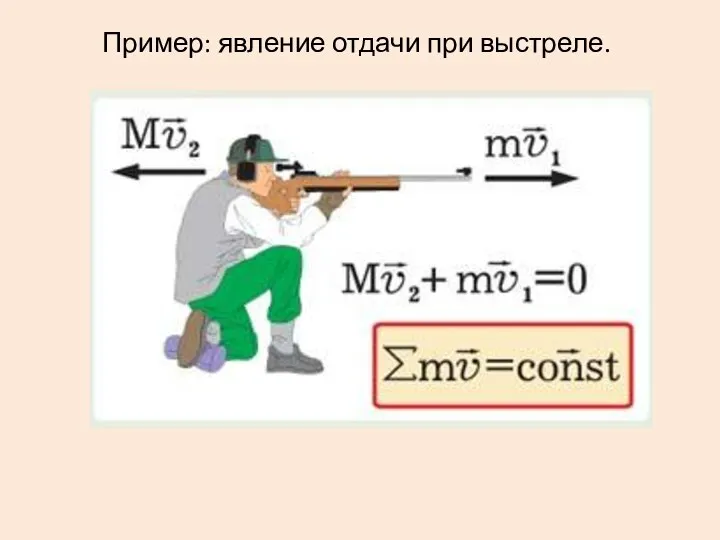
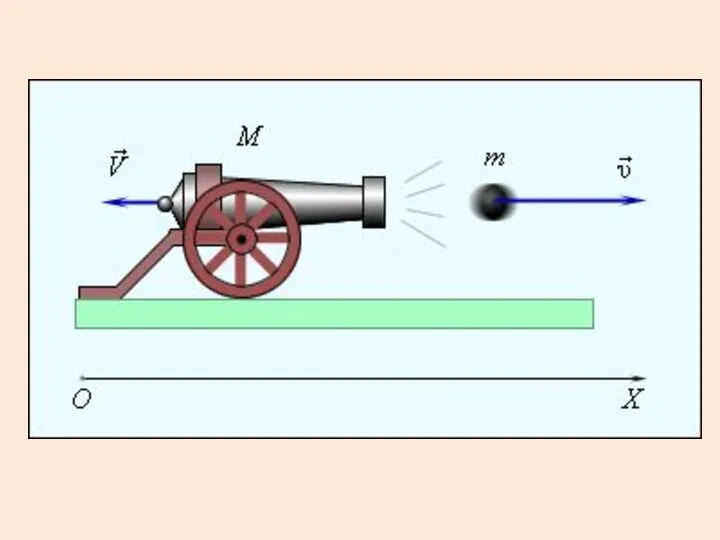
Пример: явление отдачи при выстреле.

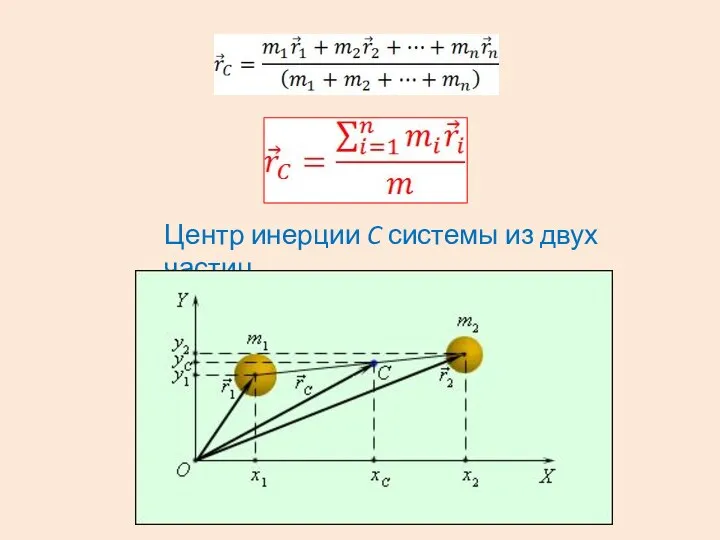
Центр инерции системы тел. Центр масс
Центром инерции системы тел называют такую точку, скорость перемещения которой, умноженная на массу всей системы, дает импульс всей системы.

Центр инерции C системы из двух частиц

Центром масс системы тел называют точку, в которую сжалась бы система покоящихся тел, подверженная только силам всемирного тяготения (при условии, что тела могли бы сжиматься до бесконечно малых размеров).

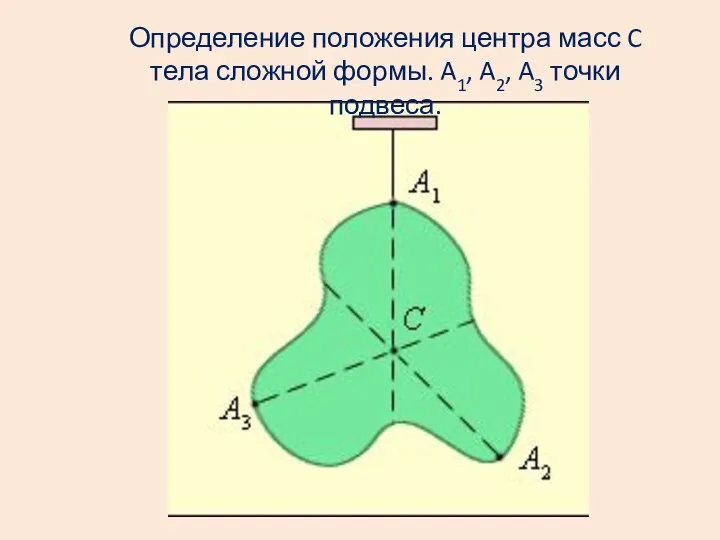
Определение положения центра масс C тела сложной формы. A1, A2, A3 точки подвеса.

Уравнение движения центра масс
Центр масс системы тел движется так, как если бы вся масса системы была сосредоточена в нем, и к нему же приложены все внешние силы.
Внутренние силы взаимодействия не могут придать какое-либо ускорение центру масс системы тел и изменить скорость его движения.

Второй закон Ньютона для тела переменной массы.
Реактивное движение.
Пусть в момент времени t=0 ракета начинает дви-жение в системе отсчета, связанной с Землей.

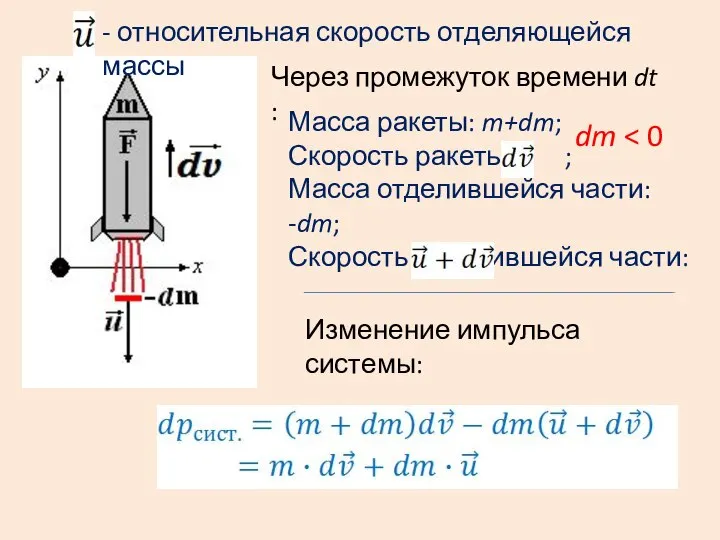
Через промежуток времени dt :
Масса ракеты: m+dm;
Скорость ракеты: ;
Масса отделившейся части: -dm;
Скорость отделившейся части:
dm < 0
Изменение импульса системы:
- относительная скорость отделяющейся массы

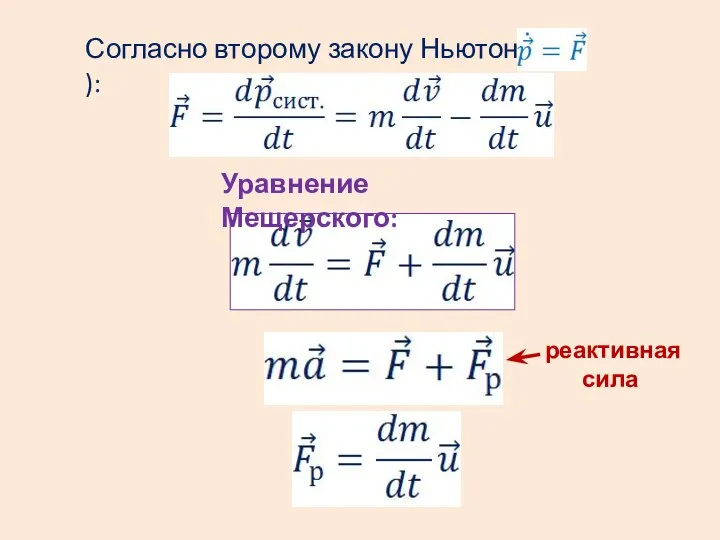
Согласно второму закону Ньютона ( ):
Уравнение Мещерского:
реактивная сила

Формула Циолковского
Пусть на тело (ракету) не действуют внешние силы: , тогда
В проекции на направление
движения:
Из начальных условий

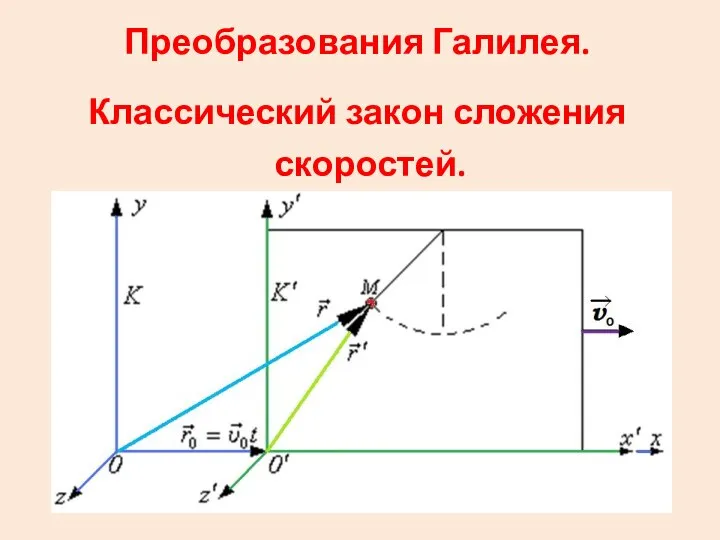
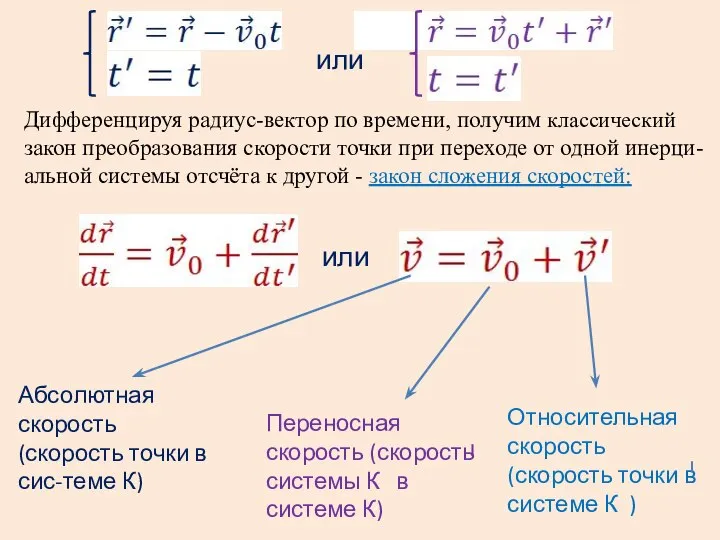
Преобразования Галилея.
Классический закон сложения скоростей.

Дифференцируя радиус-вектор по времени, получим классический закон преобразования скорости точки при переходе от одной инерци-альной системы отсчёта к другой - закон сложения скоростей:
или
или
Абсолютная скорость
(скорость точки в сис-теме К)
Переносная скорость (скорость системы К в системе К)
Относительная скорость (скорость точки в системе К )

Дифференцируя скорость по времени с учётом того, что
получим:
Ускорение точки одинаково во всех инерциальных системах отсчёта.
Принцип относительности Галилея:
в инерциальных системах отсчета все механические явления протекают одинаково.

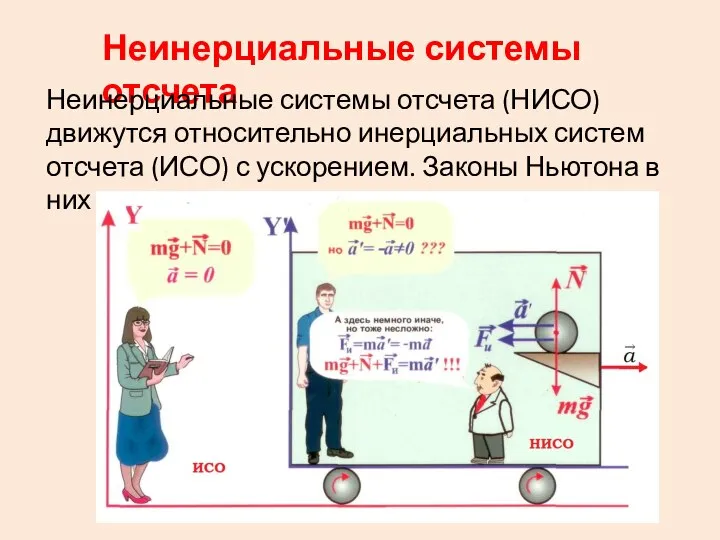
Неинерциальные системы отсчета
Неинерциальные системы отсчета (НИСО) движутся относительно инерциальных систем отсчета (ИСО) с ускорением. Законы Ньютона в них не выполняются.

Для неинерциальных систем отсчета законы динамики можно применить, если кроме сил, обусловленных вза-имодействием тел друг с другом, ввести в рассмотре-ние силы, называемые силами инерции.
Рассмотрим три различных случая:
тело находится в неинерциальной системе отсчета, движущейся поступательно;
тело покоится во вращающейся системе отсчета;
тело движется во вращающейся системе отсчета.

НИСО движется поступательно
Сила инерции
Ускорение НИСО относительно ИСО
(переносное)
Сила инерции направлена противоположно переносному ускорению системы и пропор-циональна массе тела.

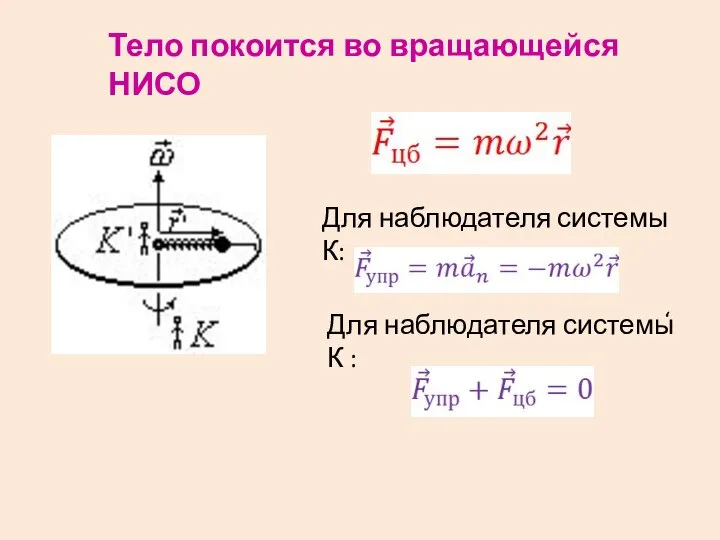
Тело покоится во вращающейся НИСО
Для наблюдателя системы К:
Для наблюдателя системы К :
‘

Тело движется во вращающейся НИСО
Наряду с центробежной силой инерции действует сила Кориолиса. Ее причина – изменение ускорения тела при его движении в НИСО.
- скорость точки во вращающейся системе отсчета.