Содержание
- 2. Цель: повторение основных понятий, законов и формул законов сохранения в соответствии с кодификатором ЕГЭ. Элементы содержания,
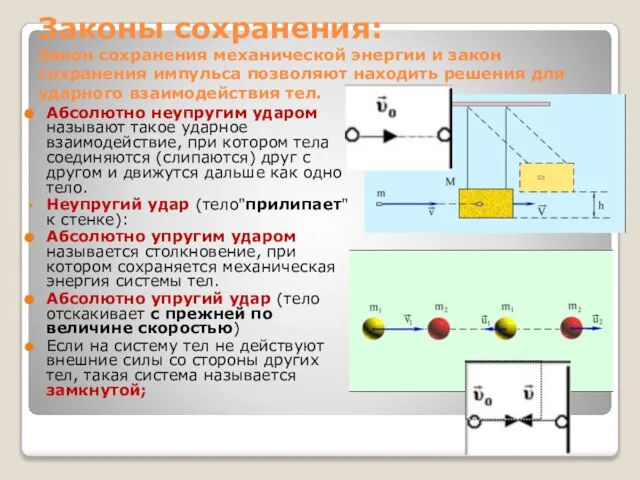
- 3. Законы сохранения: Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения для ударного взаимодействия
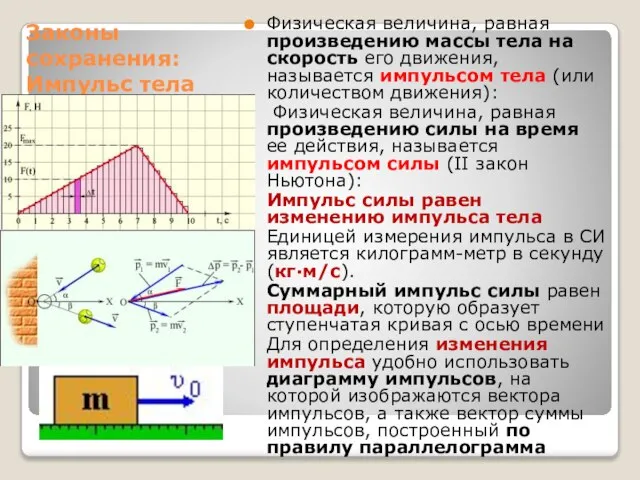
- 4. Законы сохранения: Импульс тела Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом
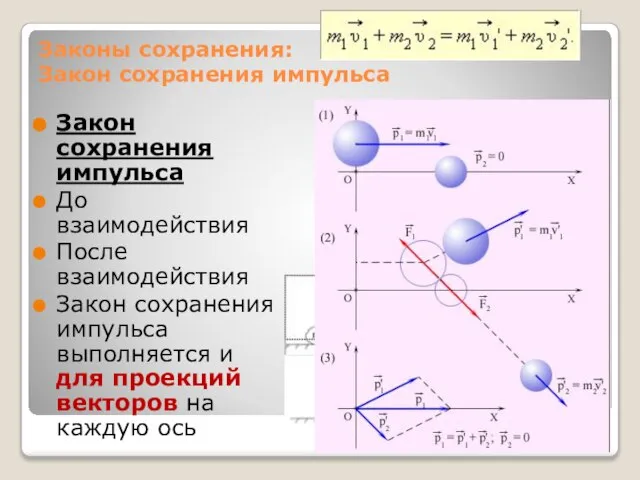
- 5. Законы сохранения: Закон сохранения импульса Закон сохранения импульса: В замкнутой системе векторная сумма импульсов всех тел,
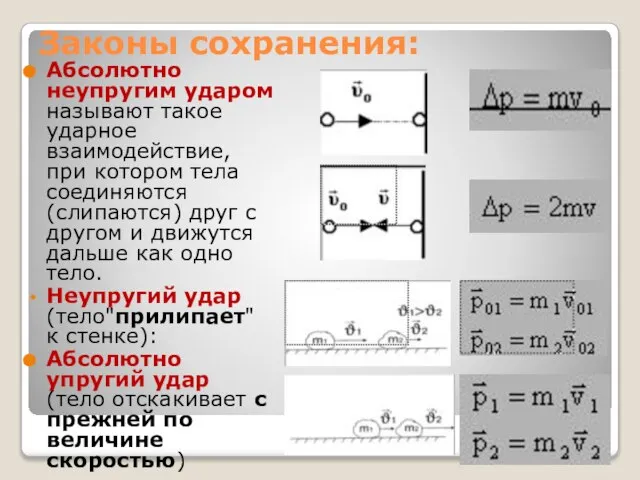
- 6. Законы сохранения: Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с
- 7. Законы сохранения: Закон сохранения импульса Закон сохранения импульса До взаимодействия После взаимодействия Закон сохранения импульса выполняется
- 8. Законы сохранения: Закон сохранения импульса - реактивное движение При стрельбе из орудия возникает отдача – снаряд
- 9. Законы сохранения: Работа силы Работой A, совершаемой постоянной силой называется физическая величина, равная произведению модулей силы
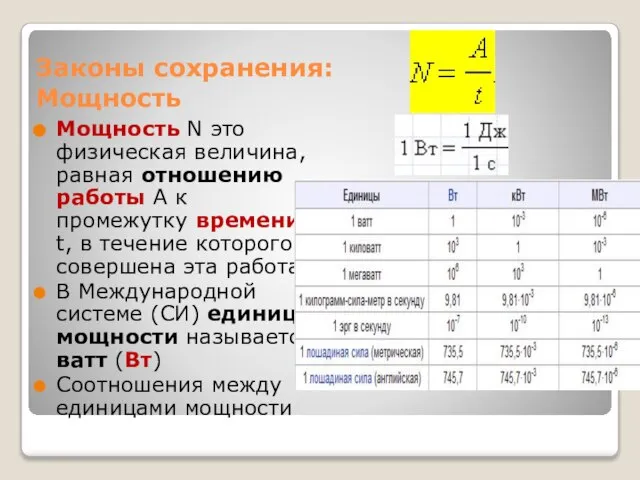
- 10. Законы сохранения: Мощность Мощность N это физическая величина, равная отношению работы A к промежутку времени t,
- 11. Законы сохранения: Кинетическая энергия Кинетическая энергия – это энергия движения. Физическая величина, равная половине произведения массы
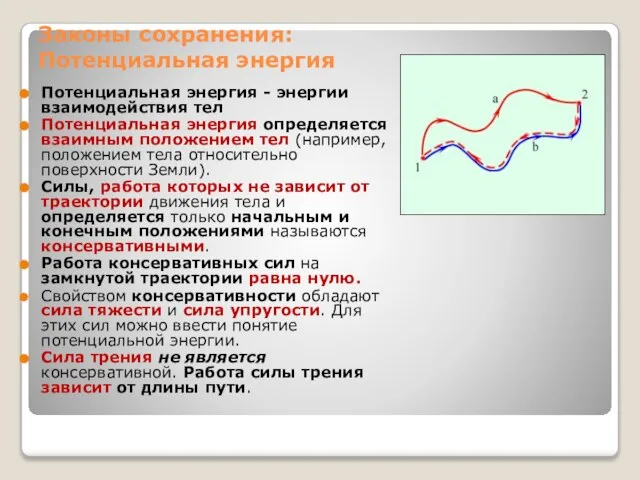
- 12. Законы сохранения: Потенциальная энергия Потенциальная энергия - энергии взаимодействия тел Потенциальная энергия определяется взаимным положением тел
- 13. Законы сохранения: Работа силы Работа силы тяжести: Когда какое-нибудь тело опускается, сила тяжести производит работу. Работа
- 14. Законы сохранения: Закон сохранения механической энергии Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и
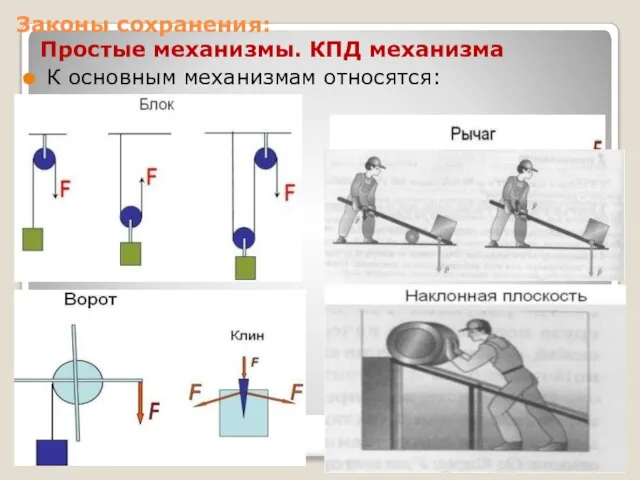
- 15. Законы сохранения: Простые механизмы. КПД механизма Основное назначение простых механизмов: Изменить силу по величине (уменьшить или
- 16. Законы сохранения: Простые механизмы. КПД механизма К основным механизмам относятся:
- 17. Законы сохранения: Простые механизмы. КПД механизма Блок - это колесо с желобом по окружности для каната
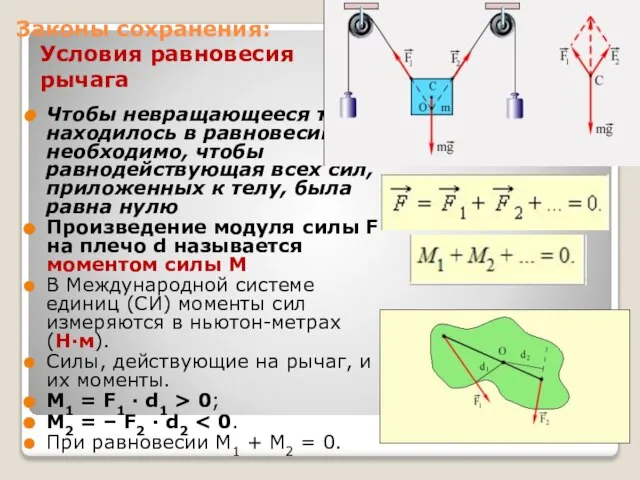
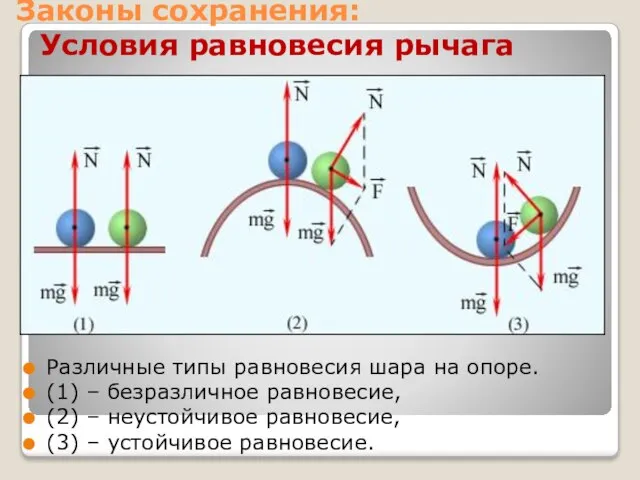
- 18. Законы сохранения: Условия равновесия рычага Плечо силы это расстояние от линии действия силы до точки, вокруг
- 19. Законы сохранения: Условия равновесия рычага Плечо силы это расстояние от линии действия силы до точки, вокруг
- 20. Законы сохранения: Условия равновесия рычага Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил,
- 21. Законы сохранения: Условия равновесия рычага Различные типы равновесия шара на опоре. (1) – безразличное равновесие, (2)
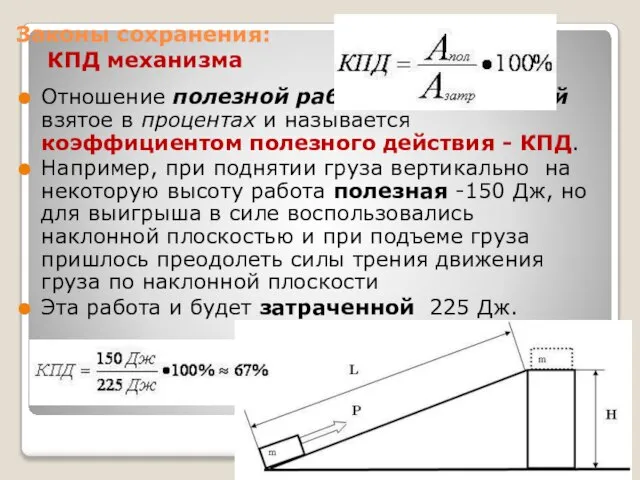
- 22. Законы сохранения: КПД механизма Отношение полезной работы к затраченной взятое в процентах и называется коэффициентом полезного
- 23. Рассмотрим задачи: ЕГЭ 2001-2010 (Демо, КИМ) ГИА-9 2008-2010 (Демо)
- 24. ГИА 2008 г. 24 Пуля массой 50 г вылетает из ствола ружья вертикально вверх со скоростью
- 25. (ГИА 2009 г.) 3. Тело, брошенное вертикально вверх с поверхности земли, достигает наивысшей точки и падает
- 26. (ГИА 2009 г.) 22. Тележка массой 20 кг, движущаяся со скоростью 0,8 м/с, сцепляется с другой
- 27. ГИА 2010 г. 3. Для придания наиболее эффективного ускорения космическому кораблю струя выхлопных газов, вырывающаяся из
- 28. (ГИА 2010 г.) 24. Транспортер равномерно поднимает груз массой 190 кг на высоту 9 м за
- 29. (ГИА 2010 г.) 25. Гиря падает на землю и ударяется о препятствие. Скорость гири перед ударом
- 30. (ЕГЭ 2001 г., демо) А3. Автомобиль массой 3000 кг движется со скоростью 2 м/с. Какова кинетическая
- 31. (ЕГЭ 2001 г.) А4. Для того, чтобы уменьшить кинетическую энергию тела в 2 раза, надо скорость
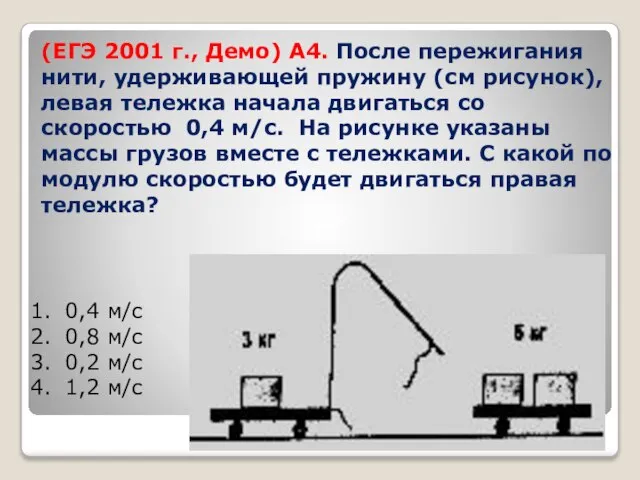
- 32. (ЕГЭ 2001 г., Демо) А4. После пережигания нити, удерживающей пружину (см рисунок), левая тележка начала двигаться
- 33. (ЕГЭ 2001 г., Демо) А5. С балкона высотой h = 3 м на землю упал предмет
- 34. (ЕГЭ 2001 г.) А6. Мужчина достает воду из колодца глубиной 10 м. Масса ведра 1,5 кг,
- 35. (ЕГЭ 2001 г.) А7. Шарик скатывали с горки по трем разным желобам. В каком случае скорость
- 36. (ЕГЭ 2001 г.) А8. Тяжелый молот падает на сваю и вбивает ее в землю. В этом
- 37. (ЕГЭ 2001 г.) А29. Два пластилиновых шарика массами m1 = 0,1 кг и m2 = 0,2
- 38. (ЕГЭ 2002 г., Демо) А5. Тележка массой m, движущаяся со скоростью v, сталкивается с неподвижной тележкой
- 39. (ЕГЭ 2002 г., КИМ) А5. Для того, чтобы уменьшить кинетическую энергию тела в 2 раза, надо
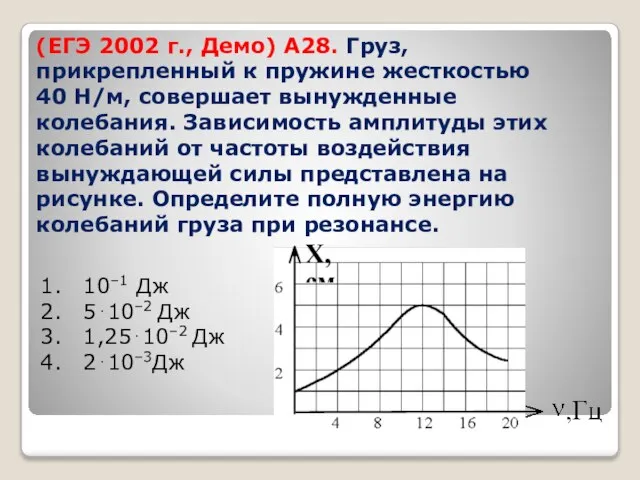
- 40. (ЕГЭ 2002 г., Демо) А28. Груз, прикрепленный к пружине жесткостью 40 Н/м, совершает вынужденные колебания. Зависимость
- 41. (ЕГЭ 2003 г., КИМ) А5. Мальчик подбросил футбольный мяч массой 0,4 кг на высоту 3 м.
- 42. (ЕГЭ 2003 г., демо) А26. Неподвижная лодка вместе с находящимся в ней охотником имеет массу 250
- 43. (ЕГЭ 2004 г., КИМ) А5. Груз массой 1 кг под действием силы 50 Н, направленной вертикально
- 44. (ЕГЭ 2004 г., демо) А21. Ракета массой 105 кг стартует вертикально вверх с поверхности Земли с
- 45. (ЕГЭ 2004 г., демо) А22. На Землю упал из космического пространства метеорит. Изменились ли механическая энергия
- 46. (ЕГЭ 2005 г., ДЕМО) А5. Потенциальная энергия взаимодействия с Землей гири массой 5 кг увеличилась на
- 47. (ЕГЭ 2005 г., ДЕМО) А7. Тело массой 2 кг движется вдоль оси ОХ. Его координата меняется
- 48. ЕГЭ – 2006, ДЕМО. А 27. Мальчик массой 50 кг, стоя на очень гладком льду, бросает
- 49. (ЕГЭ 2006 г., ДЕМО) А26. Пластилиновый шар массой 0,1 кг летит горизонтально со скоростью 1 м/с
- 50. (ЕГЭ 2007 г., ДЕМО) А6. Два автомобиля одинаковой массы m движутся со скоростями v и 2v
- 51. (ЕГЭ 2007 г., ДЕМО) А9. Скорость брошенного мяча непосредственно перед ударом о стену была вдвое больше
- 52. (ЕГЭ 2008 г., ДЕМО) А6. Шары одинаковой массы движутся так, как показано на рисунке, и абсолютно
- 53. (ЕГЭ 2008 г., ДЕМО) А9. Пластилиновый шар массой 0,1 кг имеет скорость 1 м/с. Он налетает
- 54. (ЕГЭ 2009 г., ДЕМО) А4. Легковой автомобиль и грузовик движутся со скоростями υ1 = 108 км/ч
- 55. (ЕГЭ 2009 г., ДЕМО) А5. Санки массой m тянут в гору с постоянной скоростью. Когда санки
- 56. (ЕГЭ 2010 г., ДЕМО) А4. Тело движется по прямой. Под действием постоянной силы величиной 4 Н
- 58. Скачать презентацию











































 Рассеивающие линзы
Рассеивающие линзы Закон Ома для участка цепи. Сопротивление
Закон Ома для участка цепи. Сопротивление Конвекция. Примеры конвекции
Конвекция. Примеры конвекции Ремонт и обслуживание газораспределительного механизма Камаз
Ремонт и обслуживание газораспределительного механизма Камаз Приборы для измерения температуры
Приборы для измерения температуры Наблюдение за состоянием колесных пар пассажирского вагона в пути следования
Наблюдение за состоянием колесных пар пассажирского вагона в пути следования Транспортные, транспортирующие и погрузочно-разгрузочные машины. Тема 2
Транспортные, транспортирующие и погрузочно-разгрузочные машины. Тема 2 Сравнительная характеристика электрического тока в различных средах
Сравнительная характеристика электрического тока в различных средах Машиноведение
Машиноведение Аэрогидродинамика (Лекция 1)
Аэрогидродинамика (Лекция 1) Постійний електричний струм
Постійний електричний струм Использование наноматериалов в технике
Использование наноматериалов в технике Магнитное поле
Магнитное поле Автопогрузчик H14-80 Evo серия 39X
Автопогрузчик H14-80 Evo серия 39X Две дельта - функционные ямы в импульсном представлении
Две дельта - функционные ямы в импульсном представлении Основные детали остова двигателя. Станина и цилиндры. Картеры, крепление. Вентиляция. Урок № 7. Тема 2.4
Основные детали остова двигателя. Станина и цилиндры. Картеры, крепление. Вентиляция. Урок № 7. Тема 2.4 Измерение проводника при помощи амперметра и вольтметра
Измерение проводника при помощи амперметра и вольтметра Движение по окружности
Движение по окружности Закон Архимеда
Закон Архимеда Численная модель квазистационарного электромагнитного поля, индуцируемого в проводниках с дефектами
Численная модель квазистационарного электромагнитного поля, индуцируемого в проводниках с дефектами Тепловые двигатели
Тепловые двигатели Строение и структура материалов
Строение и структура материалов Курс физики. Занятие 4. Строение вещества
Курс физики. Занятие 4. Строение вещества Презентация на тему Константин Васильев
Презентация на тему Константин Васильев  Относительность движения
Относительность движения Состав и строение атома
Состав и строение атома Кипение. Удельная теплота парообразования и конденсации
Кипение. Удельная теплота парообразования и конденсации Буровые машины для открытых горных пород. Лекция 8
Буровые машины для открытых горных пород. Лекция 8