Слайд 2Закон сохранения импульса
Законы сохранения энергии, импульса и момента импульса относятся к числу

фундаментальных принципов физики.
Они далеко выходят за рамки механики и представляют собой универсальные законы природы.
Они действуют и в области элементарных частиц, и в области космических объектов, в физике атома, в физике твердого тела и т.д
Слайд 3Закон сохранения импульса
Законы сохранения являются эффективным инструментом исследования, которым повседневно пользуются физики.

Например, если выясняется, что какой-то процесс противоречит законам сохранения, то он невозможен и не стоит пробовать его осуществить.
При помощи законов сохранения очень часто можно получить решение физической задачи простым и изящным путем. Поэтому при решении новых задач обычно принято придерживаться следующего порядка: прежде всего применяют законы сохранения, и только в случае, если этого недостаточно, переходят к решению уравнений движения.
Мы начнем изучение законов сохранения с закона сохранения импульса.
Слайд 7Силы, действующие на частицу

Слайд 8Силы, действующие на систему

Слайд 9Замкнутая система
Замкнутой (или изолированной) системы называют систему частиц, на которую не действуют

никакие посторонние тела (или их воздействие пренебрежимо мало).
Система замкнута, если внешние силы отсутствуют.
Слайд 11Закон сохранения импульса – Пример 1

Слайд 12Закон сохранения импульса – Пример 1

Слайд 13Закон сохранения импульса – Пример 2

Слайд 14Закон сохранения импульса – Пример 2

Слайд 15Закон сохранения импульса – Пример 2

Слайд 16Закон сохранения импульса – Пример 3
Кусок однородного каната висит вертикально, причем

нижний конец каната доходит до горизонтального стола.
Показать, что если верхний конец каната освободить, то в любой момент падения каната сила его давления на стол будет в три раза больше веса части каната, уже лежащей на столе.
Слайд 17Закон сохранения импульса – Пример 3
Дополнительное давление на стол (сверх веса части

каната, уже лежащей на столе) вызвано потерей импульса падающими элементами каната при их ударе о стол.
Пусть за элемент времени dt на стол падает элемент каната с массой dm = μdx,
где μ – масса, приходящаяся на единицу длины каната, a dx – элемент длины каната.
Слайд 18Закон сохранения импульса – Пример 3

Слайд 19Закон сохранения импульса – Пример 4

Слайд 20Закон сохранения импульса – Пример 4

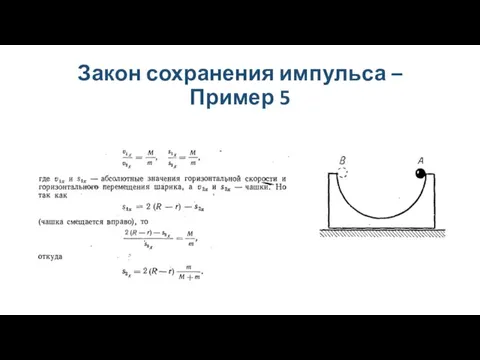
Слайд 21Закон сохранения импульса – Пример 5

Слайд 22Закон сохранения импульса – Пример 5
Слайд 28Система центра масс (Ц-система)
Когда нас интересует лишь относительное движение частиц внутри системы,

а не ее движение как целого, целесообразно пользоваться системой отсчета, в которой центр масс покоится. Эту систему называют системой центра масс или Ц – системой. Отличительной особенностью этой системы является то, что полный импульс частиц в ней всегда равен нулю.
Слайд 29Относительное движение двух частиц

Слайд 30Относительное движение двух частиц

Слайд 32Расстояния от частиц до центра масс

Слайд 36Иван Всеволодович Мещерский
русский и советский ученый-механик

Слайд 37Уравнение Мещерского-Частные случаи

Слайд 38Уравнение Мещерского-Частные случаи

Слайд 44Уравнение Мещерского – Задача 3
Ракета поддерживается в воздухе на постоянной высоте, выбрасывая

вертикально вниз струю газа со скоростью u. Найти:
1). Сколько времени ракета сможет оставаться на этой высоте, если начальная масса топлива составляет η-ю часть ее массы (без топлива);
2) Какую массу μ(t) газов должна ежесекундно выбрасывать ракета, чтобы оставаться на постоянной высоте, если начальная масса ракеты (с топливом) равна m0.

















































 Классификация композитов. Волокна и матрицы. Структура и назначение
Классификация композитов. Волокна и матрицы. Структура и назначение ТО и ТР системы питания автомобилей
ТО и ТР системы питания автомобилей Кинематика. 9 класс. Контрольная работа
Кинематика. 9 класс. Контрольная работа Струнная система с упругими опорами
Струнная система с упругими опорами Кинематика точки
Кинематика точки Применение контактных и бесконтактных аппаратов и логических элементов в схемах управления электроприводом
Применение контактных и бесконтактных аппаратов и логических элементов в схемах управления электроприводом Суд над атомом. Мультимедийный урок
Суд над атомом. Мультимедийный урок Применение законов сохранения
Применение законов сохранения Расчет расхода электрической энергии
Расчет расхода электрической энергии Ременная и цепная передачи
Ременная и цепная передачи Коронная передача
Коронная передача Радиоактивные превращения атомных ядер
Радиоактивные превращения атомных ядер Электростатика. Часть 1
Электростатика. Часть 1 Статика. Условия равновесия тел
Статика. Условия равновесия тел Подготовка к ЕГЭ
Подготовка к ЕГЭ Общие сведения о системах радиосвязи. Электропитание средств связи
Общие сведения о системах радиосвязи. Электропитание средств связи Природа звука (1)
Природа звука (1) Оптика
Оптика Закон всемирного тяготения. Исаак Ньютон
Закон всемирного тяготения. Исаак Ньютон Энергетические методы расчёта упругих систем
Энергетические методы расчёта упругих систем Исследование поверхностного натяжения жидкостей. 10 класс
Исследование поверхностного натяжения жидкостей. 10 класс Волновые свойства света
Волновые свойства света Управление образования администрации Богородского муниципального района Нижегородской области Муниципальное бюджетное образо
Управление образования администрации Богородского муниципального района Нижегородской области Муниципальное бюджетное образо Беседа Понятие об источниках тока
Беседа Понятие об источниках тока Открытия математиков в 2016 году
Открытия математиков в 2016 году Презентация на тему Опасна ли гроза
Презентация на тему Опасна ли гроза  Механические колебания и волны. Акустика
Механические колебания и волны. Акустика Зрение домашних животных
Зрение домашних животных