Затухающие и вынужденные колебания. Дифференциальное уравнение колебаний. Явление резонанса

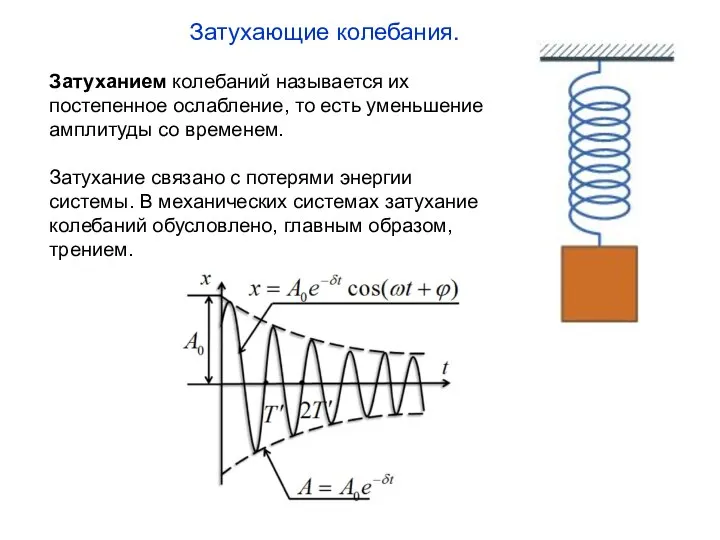
Затухающие колебания.
Затуханием колебаний называется их постепенное ослабление, то есть уменьшение амплитуды со временем.
Затухание связано с потерями энергии системы. В механических системах затухание колебаний обусловлено, главным образом, трением.

Дифференциальное уравнение затухающих колебаний
Свободные затухающие колебания в линейной системе
x = x(t) - колеблющаяся величина,
δ - коэффициент затухания,
ω0 - частота незатухающих колебаний (при δ = 0).
Колебательная система является линейной, если параметры δ и ω0 не изменяются со временем.

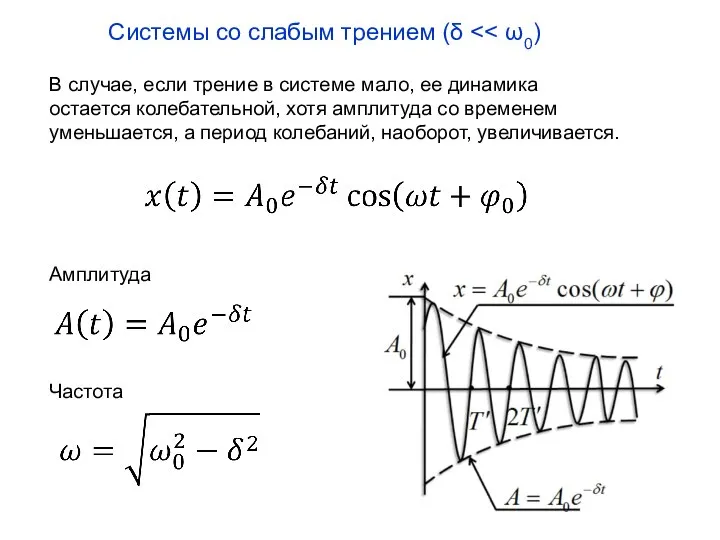
Системы со слабым трением (δ << ω0)
В случае, если трение в системе мало, ее динамика остается колебательной, хотя амплитуда со временем уменьшается, а период колебаний, наоборот, увеличивается.
Амплитуда
Частота

Время релаксации
Затухание нарушает периодичность колебаний. Однако если оно мало, то можно условно пользоваться понятием периода затухающих колебаний как промежутка времени между двумя последующими максимумами колеблющейся физической величины
Промежуток времени, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации

Декремент затухания.
Это отношение называется декрементом затухания, а его логарифм – логарифмическим декрементом затухания.
Пусть A(t) и A(t+T) – амплитуды двух последовательных колебаний, отличающихся на период. Тогда
Здесь N – число колебаний, совершаемых за время уменьшения амплитуды в e раз.

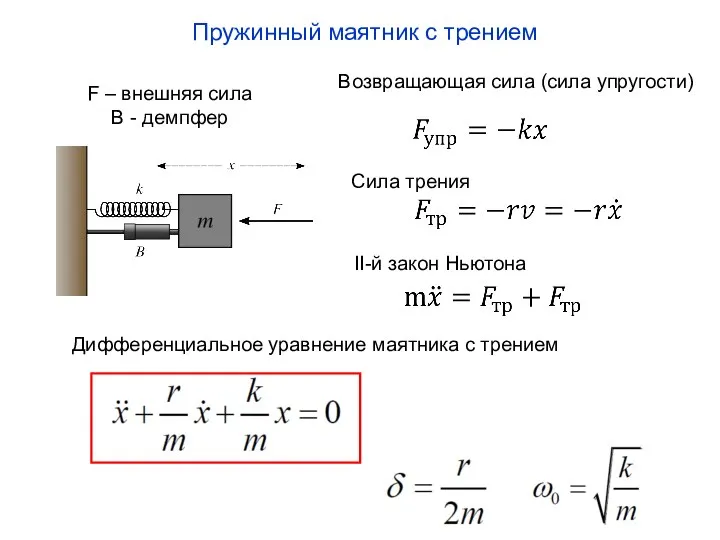
Пружинный маятник с трением
F – внешняя сила
В - демпфер
Возвращающая сила (сила упругости)
Сила трения
II-й закон Ньютона
Дифференциальное уравнение маятника с трением

Запишем ДУ в виде
Решение дифференциального уравнения
Линейное ДУ с постоянными коэффициентами – решение ищем в следующем виде
Подставляя решение в исходное ДУ, получаем характеристическое уравнение
Корни характеристического уравнения

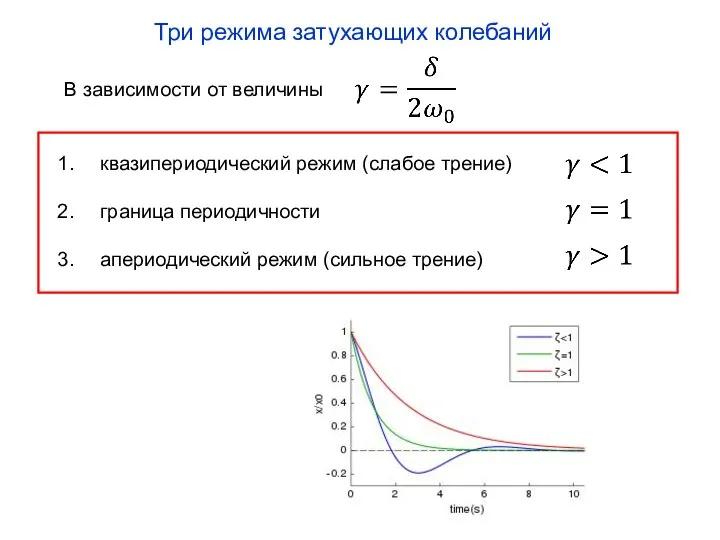
В зависимости от величины
Три режима затухающих колебаний
квазипериодический режим (слабое трение)
граница периодичности
апериодический режим (сильное трение)

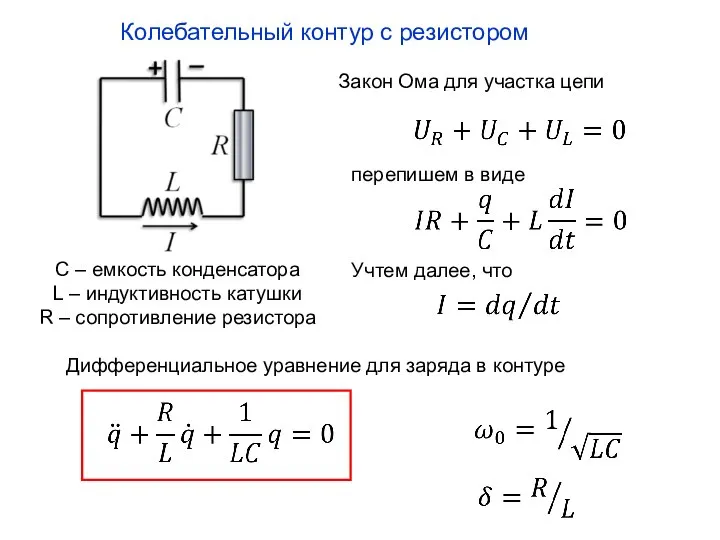
Колебательный контур с резистором
C – емкость конденсатора
L – индуктивность катушки
R – сопротивление резистора
Закон Ома для участка цепи
перепишем в виде
Учтем далее, что
Дифференциальное уравнение для заряда в контуре

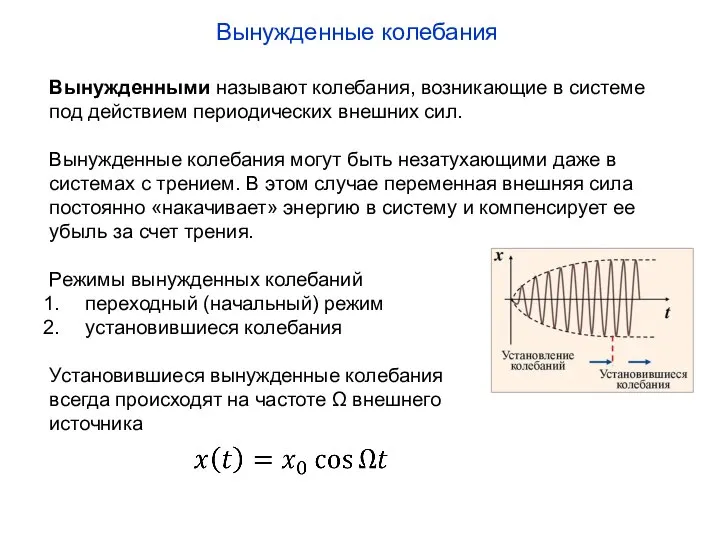
Вынужденные колебания
Вынужденными называют колебания, возникающие в системе под действием периодических внешних сил.
Вынужденные колебания могут быть незатухающими даже в системах с трением. В этом случае переменная внешняя сила постоянно «накачивает» энергию в систему и компенсирует ее убыль за счет трения.
Режимы вынужденных колебаний
переходный (начальный) режим
установившиеся колебания
Установившиеся вынужденные колебания
всегда происходят на частоте Ω внешнего
источника

Дифференциальное уравнение вынужденных колебаний
- неоднородное линейное ДУ 2-го порядка с постоянными коэф-ми. Его решение ищется в виде суммы общего решения однородного уравнения и частного решения неоднородного уравнения
Таким образом, вынужденные колебания представляют собой наложение двух видов движения: колебаний с собственной частотой ω0 и колебаний с частотой вынуждающей силы Ω.

Решения ДУ для установившихся колебаний
Амплитуда и фаза вынужденных колебаний