Физическая химия

Учебная литература
1. Стромберг А.Г., Семченко Д.П. Физ.химия. 1999.
2. Горбунов А.И. и др. Теоретические основы общей химии. 2001.
3. Еремин В.В., Каргов С.И. и др. Основы физической химии. М.:Экзамен. 2005.
4.Краткий справочник физико-химичес-ких величин» под редакцией К.П. Мище-нко и А.А. Равделя, Л.: Химия, 1974 г.

Предмет физической химии, её цели,
методы исследования
Физическая химия - пограничная наука между физикой и химией Физическая химия - наука, которая объясняет и устанавливает общие закономерности химического явления на основе законов и принципов физики с использованием физических инструментальных методов.
Нобелевский лауреат по химии Л. Полинг: "Химики - это те, кто на самом деле понимает мир”.
Термин физическая химия принадлежит Ломоносову, который впервые прочел этот курс в 1752 г. студентам Санкт-Петербургского университета.
Установленные физической химией закономерности протекания сложных процессов в химических системах используют химия, физика, биология, медицина, экология.

Физическая химия является теоретической основой для химической технологии многих отраслей народного хозяйства: производство пластмасс, синтетических волокон, лекарств, удобрений, пожаротушение и т.д.
Знание механизма и условий протекания химической реакции позволяет предвидеть их результаты и управлять химическим процессом, проводя его в нужном направлении.

Разделы физической химии
Квантовая химия изучает взаимосвязь между строением веществ, молекул и их физическими и химическими свойствами.
2. Химическая термодинамика - на основе законов общей термодинамики изучает условия, устанавливает взаимосвязь и направление течения процесса на базе энергетических характеристик веществ, а также изучает влияние различных параметров (Т, Р, С) на смещение равновесия.
3. Учение о растворах изучает природу и внутреннюю структуру растворов в зависимости от химической природы растворителя и растворенного вещества.

4. Химическая кинетика изучает влияние внеш-них факторов (температуры, давления, перемеши-вания концентрации веществ, участвующих в процессе) на скорость химических реакций.
5. Учение о катализе исследует ускорение, замедление химических реакций за счет введения в сферу реакции катализаторов или ингибиторов, т.е. управление процессом.
6. Электрохимия изучает законы взаимного превращения электрической и химической энергии, строение и свойства электролитов, работу гальванических элементов, электрохимическую коррозию металлов.
7. Фотохимия исследует влияние света на протекание химических реакций.

ЛЕКЦИЯ1 Химическая термодинамика исторически возникла на базе общей дисциплины − термодинамики, т.е. в химической термодинамике используются основные термодинамические положения и приемы применительно к описанию как химических реакций, так и физико-химических явлений (фазовые переходы веществ, процессы растворения и т.д.). Химическая термодинамика не позволяет сделать заключения о внутреннем строении веществ и о механизме протекания процесса.

ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА решает следующие задачи:
расчет тепловых эффектов процессов на основе первого закона термодинамики;
определение направления самопроизвольного протекания процесса при фиксированных внешних условиях на основе 2 закона термодинамики;
расчет констант равновесия химических реакций и определение оптимальных условий их проведения (максимизация выхода продукта) на основе 3 закона термодинамики.

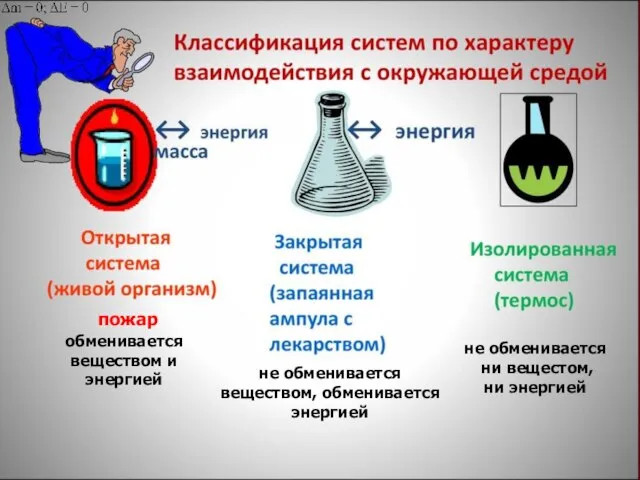
Общие понятия химической термодинамики
Термодинамическая система − это тело или группа тел, находящихся во взаимодействии и отделенных от окружающей среды реальной или воображаемой границей.
окружающая
среда

обменивается веществом и энергией
не обменивается веществом, обменивается энергией
пожар
не обменивается
ни вещестом,
ни энергией

Состояние системы характеризуется физическими и химическими свойствами (V,T, p,C). Свойства, выбранные в качестве независимых переменных, называют параметрами состояния. Их можно измерить опытным путем.
Параметры состояния, пропорциональные количеству вещества системы, называют экстенсивными (объем, масса, заряд и т.д.).
Параметры состояния, не зависящие от количества вещества, называют интенсивными (температура, давление, электрический потенциал)

Состояние системы может быть равновесным и неравновесным.
Термодинамически равновесное состояние системы – это состояние, в котором при отсутствии внешних воздействий на систему, параметры ее остаются неизменными.
Состояние системы будет неравно-весным, если при отсутствии внешнего воздействия параметры ее изменяются.

Процесс − это любое изменение параметров системы.

Различают прямой и обратный процесс. В результате прямого процесса система переходит из начального в конечное состояние, в результате обратного − из конечного в начальное.
Если прямой и обратный процессы протекают через те же промежуточные состояния, то это термодинамически обратимый процесс.
Если имеет место химическое превращение, то процесс называют реакцией.
Если система после некоторых превращений возвращается в исходное состояние, то процесс называют круговым или циклом.

- функция состояния системы

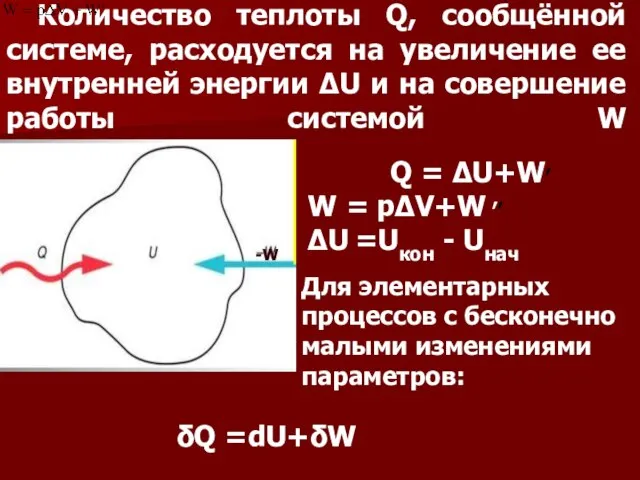
Количество теплоты Q, сообщённой системе, расходуется на увеличение ее внутренней энергии ΔU и на совершение
работы системой W
Q = ΔU+W,
W = pΔV+W ,,
ΔU =Uкон - Uнач
-W
Для элементарных процессов с бесконечно малыми изменениями параметров:
δQ =dU+δW

В термодинамике условно считают: если теплота поступает в систему, то Q берут со знаком +, со знаком −, если выделяет-ся из системы. Работу W берут со знаком +, если она совершается системой, и со знаком −, если работа совершается внешними силами.

Изотермический процесс (Т=const)
В идеальном газе отсутствуют силы взаимодейст-вия между молекулами, энергия идеального газа является функцией только температуры и не зависит ни от занимаемого объема V, ни от давления газа p, поэтому в изотермическом процессе U = const, dU = 0, V2 уравнение примет вид:
Q=W; δQT= pdV= δW
теплота, сообщенная систе- ме, расходуется на соверше- с ние работы расширения.

Изохорный процесс (V=const)
Объем системы постоянен, dV=0, работа расширения системы δW =pdV=0, тогда
QV= ΔU= Uкон – Uнач
δQ=dU
В изохорном процессе теплота, сообщенная системе, расходуется на увеличение ее внутренней энергии.
Q

Изобарный процесс (p = const)
Теплота, сообщенная системе, расходуется на увеличение ее внутренней энергии и на совершение работы против сил внешнего давления.
Qр= ΔU+pΔV = ΔН
Qр = ΔН= Нкон-Ннач
δQр = dU+pdV = d(U+рV) = dН
Н = U+рV; Н – энтальпия, функция
состояния системы, Дж/моль

Адиабатический процесс (Q = 0)
Процесс протекает при полном отсутствии теплообмена между системой и окружающей средой. Работа расширения осуществляется за счет убыли внутренней энергии системы.
pΔV = - ΔU; pdV = - dU
Это характерно для быстропротекающих процессов. Рассмотрим их.

Процесс образования облака начинается с того, что нагретый воздух, содержащий водяные пары, подни-мается вверх и быстро расширяется. Это расширение - адиабатное, так как воздух поднимается быстро. При адиабатном расширении воздух не получает теплоты извне, совершает работу только за счёт собственной внутренней энергии, поэтому охлаждается, водяные пары конденсируются, образуя облака.
Адиабатное расширение

СО22
В углекислотном огнетушителе в качестве огнетушащего вещества выступает СО2 в сжиженном виде. При выбросе его на открытый воздух он превращается в газообразное состояние, что приводит к значительному увеличению объема огнетушащего вещества и его охлаждение за счет уменьшения внутренней энергии.
Адиабатное
расширение

Тепловой эффект химической реакции
Тепловой эффект химической реакции - количество теплоты, выделяемой или поглощаемой в результате химического процесса при постоянном давлении или объеме (p = const; V = const), равенстве температур исходных веществ и продуктов реакции (Тисх.=Тпрод.) и отсутствии всех видов работ (δW,), кроме работы расширения (pΔV)

Стехиометрическое уравнение реакции, записанное с указанием теплового эффекта, агрегатных состояний исходных веществ и продуктов реакции - термохимическое.
Cт +О2(г) = СО2(г) + 402 кДж
Различают тепловой эффект реакции при постоянном объеме (Qv) и при постоянном давлении (Qp). Согласно первому закону термодинамики (Qv=ΔrU) (тепловой эффект при постоянном объеме равен изменению внутренней энергии), (Qp=ΔrH) (тепловой эффект при постоянном давлении равен изменению энтальпии).

Тепловые эффекты ΔrU0298 и ΔrН0298, приведенные к стандартным термодинамическим условиям (р=101325 Па=1 атм=760 мм рт.ст., что означает индекс “0" и Т = 298 K) называют стандартным изменением внутренней энергии и стандартным изменением энтальпии реакции.
Выделяемая теплота, т.е. убывание энергии системы, обозначается ΔrН<0.

Тепловые эффекты при постоянном давлении ΔrН0298 и постоянном объеме ΔrU0298 связаны уравнением
ΔrН0298 = ΔrU0298 + ΔrνRT
Δrν − разность количества (числа молей) газообразных веществ в правой и левой частях уравнения реакции: )
ν1А1 +ν1А1+…νiАi= ν1,B1 +ν2,B2+…νi,Bi
Δrν = (ν1, +ν2, +νi, ) - (ν1 +ν2 +νi )

Энтальпия образования и сгорания веществ
Любое сложное вещество можно гипотетически или реально синтезировать из количеств простых веществ в стандартных термодинамических условиях
С(графит)+О2(г)=СО2(г) ΔrН0298 = -393,5 кДж
Простые вещества, участвующие в реакции, должны находиться в стандартных (термодинамически наиболее устойчивых) состояниях (модификациях).

Для твердого (жидкого, газообразного) про-стого вещества при Т=298 K за стандартное состояние принимают его чистый кристалл (чистую жидкость, чистый газ) под давле-нием 101325 Па - ΔfН0298 f - formation
При существовании у вещества нескольких модификаций стандартным состоянием считают наиболее термодинамически стабильную форму. Углерод С имеет следующие модификации: алмаз,
графит,
карбин,
фуллерен,
но наиболее устойчив графит.

По определению стандартная энтальпия образования любого простого вещества в термодинамически стабильном состоянии равна нулю при любой температуре ΔfН0298 =0
Стандартные энтальпии
образования большинства
веществ приводятся в
справочниках.

Стандартная мольная энтальпия образования вещества ΔfН0298 – изменение энтальпии ΔrН0298 в реакции образования 1 моля данного вещества из простых веществ, находящихся в стандартных условиях.
Какая величина является стандартной мольной энтальпией образования СО2?
1С(графит)+О2(г)=СО2(г) ΔrН0298 = -393,5 кДж
2 С(алмаз)+О2(г)=СО2(г) ΔrН0298 = -395,5 кДж
(углерод не в стандартном состоянии)
3 СО(г)+0.5О2(г)=СО2(г) ΔrН0298 = -283 кДж
(СО – сложное вешество)

Стандартной энтальпией сгорания вещества ΔсН0298 называется изменение энтальпии в реакции окисления 1 моля вещества кисло-родом с образованием соответствующих высших оксидов в стандартных условиях (нижний индекс c - combustion − горение).
Эту величину применяют для органических веществ. При сгорании углеводородов продукты - СО2(Г),Н2О(ж)
Стандартная энтальпия сгорания О2, Н2О(ж) , газо-образного СО2и др. высших оксидов при любой температуре - ΔсН0298=0, т.к. они неспособны окисляться. При горении веществ выделяется теп-лота, поэтому ΔсН0298 <0 для всех веществ, способ-ных окисляться в кислороде, либо ΔсН0298=0 для негорючих соединений.

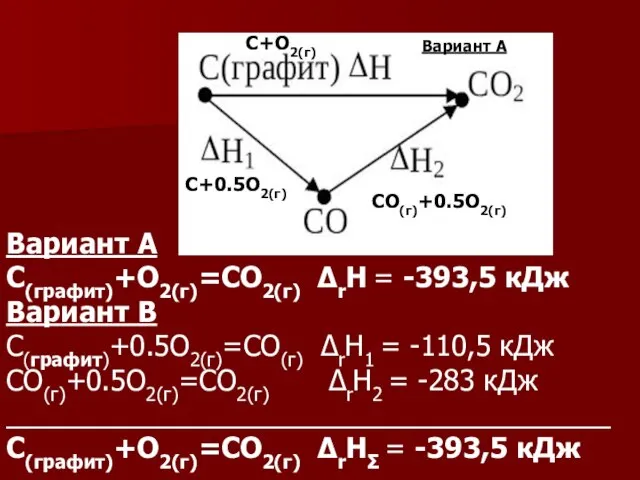
Тепловой эффект химической реакции не зависит от пути процесса (промежуточных стадий), а определяется только начальным и конечным состоянием системы, т.е. состоянием исходных веществ и продуктов реакции.
ЗАКОН ГЕССА
1836 г.

Вариант А
С(графит)+О2(г)=СО2(г) ΔrН = -393,5 кДж
Вариант В
С(графит)+0.5О2(г)=СО(г) ΔrН1 = -110,5 кДж
СО(г)+0.5О2(г)=СО2(г) ΔrН2 = -283 кДж
_______________________________________
С(графит)+О2(г)=СО2(г) ΔrНΣ = -393,5 кДж
С+О2(г)
С+0.5О2(г)
СО(г)+0.5О2(г)
Вариант А

С термохимическими уравнениями, если тепловые эффекты приводятся при одних и тех же внешних условиях, можно оперировать также, как и с алгебраическими. Их можно складывать, вычитать одно из другого. Это свойство термохи-мических уравнений вытекает из закона Гесса.
Наиболее важное значение закона Гесса состоит в том, что на его основе можно вычислить тепловой эффект реакции, экспериментальное проведение которой затруднено или невозможно. Вычисление проводят путем алгебраического комбинирования стехиометрических уравнений и тепловых эффектов реакций, изученных экспериментально.

Cледствия из закона Гесса
Первое следствие. Тепловой эффект реакции равен разности между суммой энтальпий (теп-лот) образования продуктов реакции и суммой энтальпий образования (теплот) исходных веществ с учетом их стехиометрических коэф - фициентов:
ΔrН0298 =(Σi νi ΔfН0298 )продуктов- (Σi νi ΔfН0298)исх.веществ
Второе следствие. Тепловой эффект реакции равен разности между суммой энтальпий (теплот) сгорания исходных веществ и суммой энтальпий (теплот) сгорания продуктов реакции с учетом стехиометрических коэффициентов
ΔrН0298 =(Σi νi ΔсН0298 ) исх.веществ- (Σi νi ΔсН0298)продуктов

Зависимость теплового эффекта от температуры. Закон Кирхгофа
Тепловой эффект реакции, вычисленный по первому или второму следствию из закона Гесса, относится к стандартной температуре (298 K), для которой в таблицах приводятся значения энтальпий образования или сгорания веществ. Часто необходимо знать тепловой эффект при Т, отличной от стандартной.
Прежде, чем находить зависимость теплового эффекта реакции от температуры, познакомимся с понятием теплоемкости.

Теплоемкость (С, Дж/K) - отношение количества сообщенной теплоты веществу (системе) dQ к наблюдаемому повышению температуры dT в отсутствие химических реакций, фазовых переходов, полезной работы dW,
С = dQ/dT, Дж/K

с= C/m
с= C/n
Дж/кг. K
Дж/моль . K

В зависимости от условий нагревания вещест-ва в соответствии с определением теплоем-кости и первым законом термодинамики
для изобарного процесса Ср = dH/dT
изохорного Cv= dU/dT (Дж/моль·K).
Для 1 моля идеального газа H = U + pV = U + RT
CP = CV + R.
Для конденсированных веществ (жидкостей и твердых веществ)
Ср ≈ Cv.

Выведем зависимость ΔН0T=f(T) для реакции
ν1А1 + ν2А2→ ν’1А’1 + ν’2А’2
Пусть Hi и Hi , - мольные энтальпии при температуре Т i-того реагента и продукта.
При необратимом протекании реакции, когда вещества реагируют в количествах, равных их стехиометрическим коэффициентам, т.е. из ν1 и ν2 моль исходных веществ образуется ν1, и ν ,2 молей продуктов реакции.
Вычислим изменение энтальпии в процессе
ΔrH0T=(ν’1Н’1 +ν’2Н’2)прод.- (ν1Н1+ν2Н2)исх. =
=Σ ν’iН’i - Σ νiНi

При протекании реакции при постоянном давлении ее тепловой эффект Qp=ΔrH0T. Продифференцируем уравнение по температуре при р = const:
При невысоких давлениях частную производную можно заменить на полную
d(ΔrH0T)/dT= ΔCp.

Если реакция протекает при постоянном объеме, для нее справедливо уравнение
d(ΔrU0T)/dT= ΔCv.
Эти выражения - уравнения Кирхгофа показывают зависимость теплового эффекта реакции от температуры.
Большинство процессов идет при постоянном давлении, поэтому используют d(ΔrH0T)/dT= ΔCp.
Величина ΔCp играет роль температурного коэффициента в этой зависимости, т.е. пре-дставляет изменение теплового эффекта при изменении температуры на 1K

Влияние температуры на тепловой эффект определяется знаком величины ΔCp:
а) если ΔCp> 0, то производная положитель-на, что свойственно возрастающей функции, т.е. ΔrH0T увеличивается с ростом Т;
б) если ΔCp< 0, то производная отрицате-льна, это характерно для убывающей функции, т.е. ΔrH0T уменьшается с ростом Т;
в) если ΔCp= 0, то производная равна нулю ΔrH0T = const и не зависит от температуры.
Для расчетов интегрируют уравнение d(ΔrH0T)/dT= ΔCp и получают уравнение Кирхгофа в интегральной форме:

В качестве нижнего предела обычно берут Т1=298 K, т.к ΔrH0298 легко вычислить по след-ствиям из закона Гесса. Для расчета ΔrH0Т2 необходимо знать зависимость ΔCp=f (T), т.е. теплоемкость каждого реагента и продукта как функцию температуры.

ЗАВИСИМОСТЬТЕПЛОЕМКОСТИ ОТ ТЕМПЕРАТУРЫ
Теплоемкость индивидуального вещества увеличивается с ростом температуры. Зависимости теплоемкости веществ определены эк-спериментально и записываются степенными рядами:
Они справедливы в определенном температурном интервале. В справочных таблицах для каждого вещества приведены коэффициенты а, b, c, c’.

Зависимость ΔCp в реакции от Т имеет вид:
ΔCp =Δa + ΔbT +ΔcT2
Δa=(ν’1а’1 + ν’2а’2) - (ν1а1 + ν2а2)=Σ ν’iа’i - Σ νiаi
Подставим ΔCp в уравнение Кирхгофа
Т
ΔrH0T= ΔrH0298+0Т 298 (Δa+ΔbT +ΔcT2)dT
Для практических расчетов применяют следующие приближения:
ΔrH0T= ΔrH0298 = const
2. принимают ΔCp= ΔC0p,298= const, тогда
ΔrH0T= ΔrH0298+ ΔCp (T – 298)

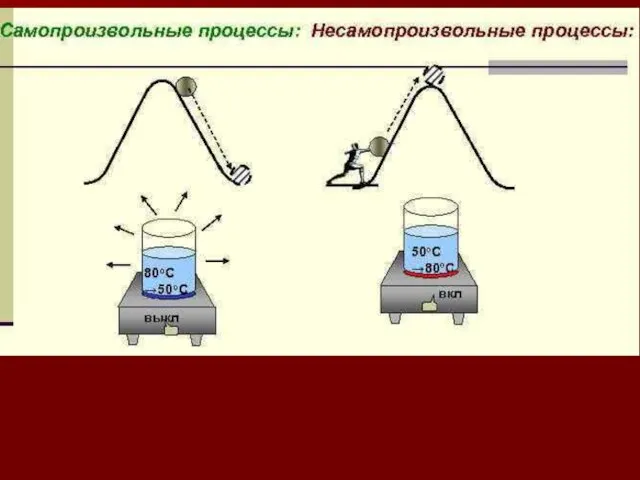
САМОПРОИЗВОЛЬНЫЕ И НЕСАМОПРОИЗВОЛЬНЫЕ ПРОЦЕССЫ
Химические реакции делят на самопроизвольные, т.е. протекающие без подвода энергии от внешнего источника, и несамопроизвольные, для проведе-ния которых необходима энергетическая подпитка.
Самопроизвольные - окислительно-восстановите-льные реакции, идущие в гальванических элементах.
Несамопроивольные - фотосинтез в листьях растений под действием солнечной энергии.

Основным при изучении закономерностей химических процессов является вопрос о направлении самопроизвольных реакций. В XIX веке сформулирован принцип Бертло: самопроизвольные процессы сопровождаются выделением тепла, т.е. экзотермические.
В природе − экзотермические: горение, гниение органических веществ.
Величину изменения энтальпии ΔН для оценки возможности прохождения реакции использовать невозможно.

1.Например, реакции растворения многих веществ эндотермические, процесс идет самопроизвольно
K2SO4(т)→ K2SO4(р-р) ΔН0298 =26.8 кДж/моль
2. Распространение запаха летучих компонентов (смешение газов) не сопровождается выделением или поглощением энергии.
Т.е. на основе 1 закона термодинамики нельзя сделать вывод о направлении процесса.
Вопрос о направлении и условиях самопроизволь-ного проте­кания процессов решается в рамках второго начала термодинамики, впервые (1850 г.), сформулированного Клаузиусом.

ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
Т1 > Т2
Т2
Т1

W
ФОРМУЛИРОВКА ТОМСОНА 1851 Г.

− функция состояния системы
Понятие энтропии введено в 1865 году Клаузиусом. Он определил изменение энтропии термодинамичес-кой системы при обратимом процессе как отношение количества тепла ΔQ к абсолютной температуре Т, ΔS = ΔQ /T, Дж/K
необрат

В обратимом процессе – Т.к. работа, совершаемая в
необратимом процессе всегда меньше, чем в обратимом, то
После объединения эти уравнения примут вид
или TdS ≥ δQ.
Подставив δQ из первого закона термодинамики, получим неравенство: TdS ≥ dU + pdV.
В изолированной системе U и V - const, т.е. dU = 0, dV=0, получим TdS ≥ 0, но Т > 0, поэтому dS ≥ 0.

В изолированной системе знак изменения энтропии является критерием направлен-ности самопроизвольного процесса.
а). Если ΔS = 0 (S = Smax т.е. достигает своего максимального значения), то система находится в состоянии термодинамического равновесия;
б). Если ΔS > 0 (S → Smax энтропия возрастает до максимального значения), процесс самопроизвольно протекает в прямом направлении, т.е. термодинамически возможен;
с). Если ΔS <0 (S → Smin энтропия убывает), то самопроизвольно может протекать лишь обратный процесс, прямой процесс термодинамически невозможен.

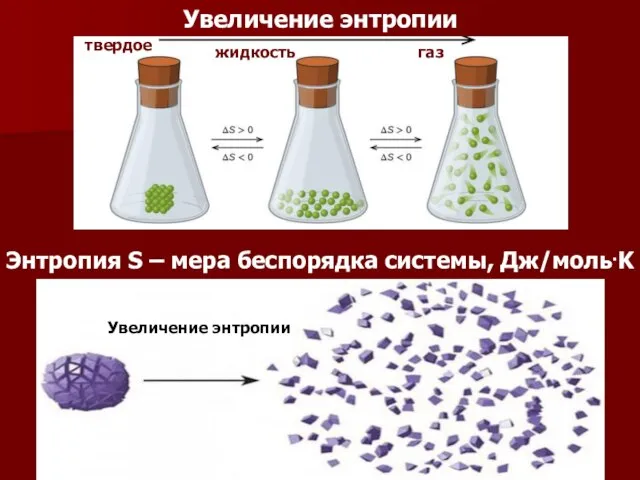
Энтропия S – мера беспорядка системы, Дж/моль.K
Увеличение энтропии
мера
твердое
жидкость
газ
Увеличение энтропии

Только возрастанием энтропии можно объяснить самопроизвольное протекание процессов в изолированных системах :
передача теплоты от более нагретого тела к менее нагретому
2. взаимную диффузию (смешение) двух или нескольких химически не взаимодействующих газов.

ИЗМЕНЕНИЕ ЭНТРОПИИ В НЕКОТОРЫХ
ПРОЦЕССАХ
1. При фазовых переходах процесс осуществляется в изобарно-изотермических условиях (р,T = const)
ΔtrsS= S2- S1 = Qp/T =ΔtrsH/T
ΔtrsH − молярное изменение энтальпии (моляр-ная теплота) при фазовом переходе (transition), T − температура фазового перехода.
2. Изменение энтропии 1 моля идеального газа а) в изохорном процессе (V = const) при нагреве от Т1 до Т2: TdS =δQ=dU=CV dT
dSV=CV(dT/T); ΔSV=T1ƒT2CV(dT/T).
Если принять Cv=const в интервале температур T1-T2 : ΔSV=CVln(T2/T1)

б) изобарный (р = const) нагрев от T1 до Т2, получаем: TdS =δQP=dH=CPdT
Интегрируя dSP=CP(dT/T) и принимая CP=const в интервале температур T1 - T2, получаем ΔSP=CPln(T2/T1), Дж/моль·K.
в) изотермическое (Т=const) расширение объема от V1 до V2 (для идеального газа при T=const, U= const, dU = 0): TdS=δQ=pdV.
Для 1 моля идеального газа p=RT/V, тогда
dST=(P/T)dV= RdV/V. После интегрирова-ния получим ΔST=Rln(V2/V1) =Rln(p1/p2)
Если количество вещества в системе n моль, то умножаем на n молей, ΔS получаем в Дж/K.

ИЗМЕНЕНИЕ ЭНТРОПИИ ПРИ СМЕШЕНИИ
химически не взаимодействующих идеальных газов ΔmixS.
Представим изолированную систему − цилин-дрическую капсулу объемом V, состоящую из k разных по объему Vi ячеек, разделенных перегородками.
В каждой ячейке содержится ni молей инертного идеального газа, у всех газов р,Т=const. Так как объемы Vi отличаются друг от друга, в соответствии с законом Авогадро число молей ni пропорционально объему Vi. Число молей ni различно.

При удалении перегородок самопроизвольно начинается взаимная диффузия газов (смешение), происходящая пока молекулы каждого газа равномерно не распределятся по всему объему V капсулы.
Так как газы не вступают в химическую реакцию, Т=const, т.е. процесс рассматривают как изотермическое расширение от Vi до V=ΣiVi.
В соответствии с интегральным уравнением для энтропии запишем:
ΔmixS = RΣinilnV/Vi.

У идеальных газов, находящихся при одинако-вых P и T объемные (φi) и молярные (Ni) доли равны φi=Vi/V = ni/n= Ni, а Σi φi= Σi Ni)=1. Преобразуем уравнение изменения энтропии при смешении ln(Vi/V)=-ln(V/Vi)= -lnNi;
ΔmixS = -RΣinilnNi.
Умножим и разделим правую часть уравнения на число молей газов n, которое можно внес-ти под знак суммы Σ и получим
ΔmixS = -nRΣiNilnNi (Дж/K),
ΔmixS >0 - при смешении газов энтропия системы возрастает.

При температуре абсолютного нуля (Т = 0 K) энтропия идеальных кристаллов любого простого вещества или соединения равна нулю.
ТРЕТИЙ ЗАКОН ТЕРМОДИНАМИКИ

Принцип недостижимости абсолютного нуля: при приближении температуры к абсолютному нулю тепловые свойства тел перестают зависеть от температуры, поэтому абсолютный нуль недостижим.
Стандартное значение энтропии определяют для чистого твердого вещества (жидкости, газа) при стандартных термодинамических условиях (р=101325Па=1атм, Т=298 К) и записывают S0f,298.
Стандартная энтропия любого вещества S0298 - величина положительная, изменение энтропии в процессах может быть положительным, отрицательным и равным нулю.

АБСОЛЮТНОЕ ЗНАЧЕНИЕ ЭНТРОПИИ
Если вещество при Т=0 K находится в виде чистого кристалла, его энтропия S=0.
Для определения энтропии этого вещества в газообразном состоянии при Т и р=101525 Па с веществом произойдет ряд превращений:
1. нагрев от Т=0 K до Тпл.;
2. плавление, т.е. перевести вещество из твердого в жидкое состояние;
3. нагрев от Тпл. до Ткип
4. испарение, т.е. перевести вещество из жидкого в газобразное состояние;
5. нагрев от Ткип до Т.

С­ртв, С­рж, С­рг− изобарные теплоемкости веществ в твердом, жидком и газообразном состояниях; ΔН­пл , ΔН­кип− теплоты плавления и кипения при температурах плавления Тпл и кипения Ткип.
Для определения энтропии этого вещества в жидком состоянии при Т и р=101525 Па используют первые 3 слагаемых.

Так как энтропии – функция состояния ее изменение в реакции в стандартных условиях рассчитывают так
ΔrS0298=Σi νiS0298(прод) - Σi νiS0298(ис.в-в)
Изменение энтропии в химической реакции при Т, отличной от 298 K, рассчитывают как
ΔrS0Т= ΔrS0298+ ∫ T298 (ΔСр/T)dT
При ΔСр=const ее можно вынести за знак интеграла, после интегрирования получим
ΔrS0Т= ΔrS0298+ ΔСрln(T/298)

ИЗМЕНЕНИЯ ЭНЕРГИИ ГИББСА И ГЕЛЬМГОЛЬЦА − КРИТЕРИИ НАПРАВЛЕННОСТИ САМОПРОИЗВОЛЬНОГО ПРОЦЕССА В ЗАКРЫТОЙ СИСТЕМЕ
В ходе процесса в системе изменяется как энер-гия, так и энтропия, поэтому необходимо ввести критерий, включающий обе составляющие.
Реальные процессы происходят в закрытых системах , в которых не происходит обмена массой, но происходит обмен энергией с окружаещей средой.

Критерием направленности самопроизвольного процесса в закрытой системе
при р,Т= const – ΔG; при V,Т= const - ΔF
Гельмгольц, Герман
Людвиг Фердинанд
(1821-1894)
Функцией, учитывающей оба этих
фактора при р,Т = const, является энергия
Гиббса G (изобарно-изотермический потенциал)

TΔS - связанная энергия, т.е. часть полной энергии системы, которая рассеивается в окружающей среде в виде теплоты (потерянная работа).
Энергия Гиббса и Гельмгольца - часть полной энергии системы, которая может быть превращена в работу в изобарно-изотермическом или изохорно-изотермическом процессах (полезная работа). Энергия Гиббса и Гельмгольца − функции состояния системы, их абсолютные значения не поддаются вычислению.

Для химической реакции изменение энергии Гиббса при переходе системы из состояния 1 в состояние 2: ΔrG =G2-G1 при постоянном дав-лении (p=101325 Па) ΔrG0Т= ΔrH0Т -Т ΔrS0Т
уравнение Гиббса-Гельмгольца
Изменение энергии Гиббса химической реак-ции связано с тепловым эффектом и темпе-ратурой, т.к. ΔrH0Т=f(Т)≠const ; ΔrS0Т=f(Т)≠const, показывает, что знак и величина энергии Гиббса зависит от двух факторов энтальпийного (энергетического) и энтропийного.

От соотношения этих факторов зависит термодинамическая возможность самопроизвольного протекания реакции в закрытой системе при р, T=const
С одной стороны в ходе химической реакции система стремится прийти к минимальному уровню внутренней энергии, выделив часть ее в форме теплоты или работы (ΔrH0Т <0), с другой -система стремится занять наиболее вероятное состояние с максимумом беспорядка, т.е. максимумом энтропии - ΔrS0Т >0.

ΔrG0Т= ΔrH0Т -Т ΔrS0Т Рассмотрим варианты, возможные при проведении химических реакций:
а) ΔrH0Т <0; ΔrS0Т > 0, то ΔrG0Т <0 при всех значе-ниях температуры, процесс термодинамически возможен при любой температуре;
б) ΔrH0Т <0; ΔrS0Т < 0, тогда ΔrG0Т <0 при Т< ΔrH0Т/ΔrS0Т; т.е. реакция термодинамически возможна в низкотемпературном режиме;
в) ΔrH0Т > 0; ΔrS0Т > 0, тогда ΔrG0Т <0 при Т> ΔrH0Т /ΔrS0Т - процесс термодинамически возможен при высоких температурах;
г) ΔrH0Т > 0; ΔrS0Т < 0 , тогда ΔrG0Т > 0 - − оба фактора действуют в неблагоприятном направлении, реакция невозможна при любых температурах.

Поскольку энергия Гиббса является функцией состояния системы, возможен ее расчет по станда-ртным энергиям Гиббса образования продуктов реакции и исходных веществ
ΔrG0298 =(Σi νi ΔfG0298 )продуктов- (Σi νi ΔfG0298)исх.веществ
Стандарная энергия Гиббса образования ΔfG0298 - изменение энергии Гиббса в реакции обра-зования 1 моля соединения из простых веществ, находящихся в термодинамически устойчивых модификациях при стандартных условиях.
ΔfG0298 =0 для простых веществ, находящихся в термодинамически устойчивых состояниях, а для сложных - в справочнике, а если ее нет, можно рассчитать ΔfG0298= ΔfH0298 – 298 S0f,298

ТЕРМОДИНАМИКА РАСТВОРОВ
Характеристика растворов и их классификация
Раствор − гомогенная система, состоящая из двух или большего числа компонентов, состав которой может изменяться.
По агрегатному состоянию растворы различают
твердые (сплавы, минералы),
жидкие растворы (соль, сахар в воде).
газообразные (воздух).
На практике чаще имеют дело с жидкими растворами.
Жидкие растворы получают смешением жидкостей, растворением твердых веществ и газов в жидкостях, плавлением твердых систем, содержащих более одного компонента.

В жидких растворах различают растворитель и растворенное вещество.
Вещество, присутствующее в растворе в большем количестве, называют растворителем (1).
Остальные вещества, присутствующие в растворе, называют растворенное вещество (2). Если вещества взяты в одинаковых количествах, то растворитель - это вещество, агрегатное состояние которого совпадает с состоянием раствора.
Различают идеальные, разбавленные и неидеальные растворы.

В идеальном растворе
а) силы взаимодействия между молекулами разных видов равны силам взаимодействия между молекулами одного вида;
б) смешение компонентов происходит без поглощения или выделения теплоты (ΔН = 0) и без изменения объема (ΔV = 0), т.е. так, что объем раствора равен сумме объемов компонентов.
Образование раствора из компонентов − процесс самопроизвольный, в котором, как и в самопроизвольном процессе, протекающем в закры-той системе под влиянием двух факторов р и Т:
1. энергия Гиббса уменьшается ΔG<0;
2. энтропия возрастает ΔS > 0.

Идеальные растворы могут образовываться из веществ, молекулы которых, сходны по полярности, строению, химическому составу. Примеры идеальных растворов: изотопы, изомеры, смеси ряда гомологов.
Термодинамические характеристики идеального раствора выражают через парциальные мольные величины:
ΔG = N1ΔG1 + N2ΔG2; ΔV = N1ΔV1 + N2ΔV2
Предельно разбавленные − растворы, в которых концентрация растворенного вещества бесконечно мала.
Неидеальные − растворы, не подчиняющиеся закономерностям идеальных и предельно разбавленных растворов. Равновесные свойства неидеальных растворов определяют эмпирически.
По наличию или отсутствию электролитической диссоциации растворы подразделяют на электролиты и неэлектролиты.

Способы выражения концентраций растворов
Для характеристики раствора используют понятия состав раствора или концентрация компонентов. Различают несколько способов выражения концентрации:
доля компонента в растворе (массовая, объемная, молярная) определяется отношением количества данного компонента (по массе, объему или числу молей) ко всему количеству раствора.
Массовая доля компонента Wi = mi/Σmi
Объемная доля φi = Vi/ΣVi
Молярная доля i-го компонента (Ni) - отношение числа молей i− го компонента (ni;) к сумме числа молей всех компонентов в растворе (Σni): Ni = ni/Σni
Wi, φi, Ni - могут изменяться от 0 до 1.

Молярность (С2) − число молей растворенного вещества в 1 л раствора: С2=n2/V
n2 − число молей растворенного вещества; V − объем раствора, л(дм3)
Моляльность (m2) − число молей, растворенного вещества в 1 кг растворителя m2= (n2/g1)×1000
n2 − число молей растворенного вещества; g1 − масса растворителя, г; 1000 − коэффициент перерасчета из г в кг.

Термодинамическая теория растворов
Основной вопрос термодинамической теории растворов - установление зависимости равновесных свойств растворов от состава и свойств его компонентов.
Для реальных растворов термодинамической теории до настоящего времени не создано. Существует теория для идеальных растворов.
При анализе результатов измерений давления насыщенного пара растворов в 1884 г. Рауль обнаружил закономерность:
при постоянной температуре (Т = const) равновесное парциальное давление каждого компонента (pi) равно давлению этого компонента в чистом виде (рi0) при данной температуре, умноженному на его мольную долю (Ni), в растворе, т.е. pi= рi0 Ni.
Раствор - идеальный, если он подчиняется закону Рауля во всей области концентраций от Ni = 0 до Ni = 1 при всех Т и р .

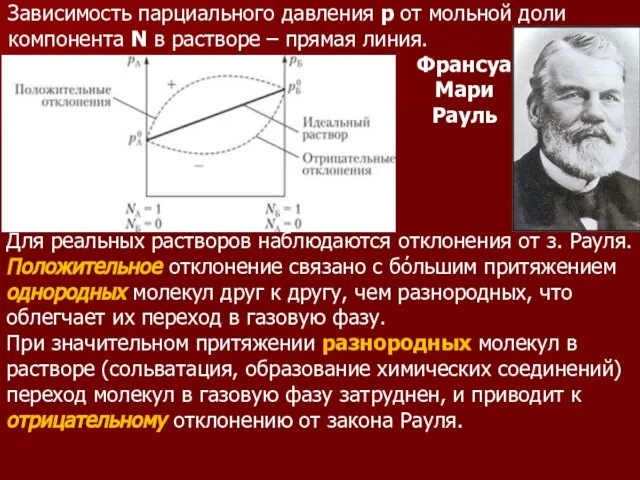
Зависимость парциального давления р от мольной доли компонента N в растворе – прямая линия.
Для реальных растворов наблюдаются отклонения от з. Рауля. Положительное отклонение связано с бόльшим притяжением однородных молекул друг к другу, чем разнородных, что облегчает их переход в газовую фазу.
При значительном притяжении разнородных молекул в растворе (сольватация, образование химических соединений) переход молекул в газовую фазу затруднен, и приводит к отрицательному отклонению от закона Рауля.
Франсуа
Мари
Рауль

Если идеальный раствор состоит из двух летучих компонентов, то закон Рауля справедлив для растворителя p1= р10 N1 и растворенного вещества p2= р20 N2.
Общее давление пара над идеальным раствором равно сумме парциальных давлений отдельных компонентов - закон Дальтона р= p1+ p2= р10 N1 +р20 N2. Т.к. N1 +N2 =1
р= р10 N1 +(р20 - р10) N2
В предельно разбавленных растворах, когда концентрация растворенного вещества, бесконечно мала, давление пара растворителя следует закону Рауля: p1=р10 N1= р10(1- N2)

Растворенное вещество не подчиняется закону Рауля, а следует закону Генри: при постоянной температуре парциальное давление пара растворенного жидкого (газообразного) вещества пропорционально его мольной доле p2=K2 N2
K2 − константа Генри, зависит от природы компонентов раствора и температуры, но не зависит от давления.
Т. о., в теории предельно разбавленных растворов проводится выделение основного компонента − раство-рителя, из всех компонентов, образующих раствор.
Поэтому эта теория идеально подходит для выяснения вопроса о влиянии примесей на свойства чистого растворителя: изменение температуры замерзания и кипения, появление осмотического давления.

Температура кипения разбавленных растворов
нелетучих веществ. Эбулиоскопия
Жидкость начинает кипеть, когда давление ее на-сыщенного пара равно внешнему давлению.
Установлено, что давление пара над раствором нелетучего вещества Р1 ниже, чем над чистым растворителем р10.
Поэтому температура кипения раствора Т1 выше температуры кипения чистого растворителя Т10. Разность температур Т1-Т10=ΔТкип характеризует повышение температуры кипения раствора.
р1
р10

Опытным путем Раулем было найдено, что в бесконечно разбавленных растворах, повышение температуры кипения пропо-рционально концентрации раствора:
ΔТкип=Т1- Т10=КЭm2=КЭ(g2×1000)/(g2×М2)
m2 − моляльность раствора; g1, g2 − навески растворителя и растворенного вещества; М2− молярная масса растворенного вещества.
КЭ − эбулиоскопическая постоянная

Эбулиоскопическая постоянная (Kэ) характеризует природу растворителя и не зависит от природы растворенного вещества.
Приведенное уравнение справедливо для бесконечно разбавленных неэлектролитов, например, глюкозы C6H12O6.
Растворы электролитов вследствие диссоциа-ции растворенного вещества дают более высокую температуру кипения. Поэтому в уравнение вносят изотонический коэффициент (i >1)
ΔТкип =Т1- Т10= i КЭm2
NaCl = Na+ + Cl− i =2
Na2SO4 =2 Na+ + SO42− i = 3
Na3PO4 =3 Na+ + PO43− i = 4

Эбулиоскопия − метод исследования растворов, основанный на измерении повышения их температуры кипения по сравнению с чистым растворителем. Используют для определения молекулярной массы растворенного вещества.

Температура замерзания разбавленных растворов. Криоскопия
Жидкость начинает кристаллизоваться, когда давление насыщенного пара над раствором и над твердым растворителем будет одинаковым.
Рауль показал, что в бесконечно разбав-ленных растворах разность между темпера-турами замерзания чистого растворителя Т10 и раствора Т1 (ΔТзам = Т10 - Т1) пропорциональна концентрации растворенного вещества в растворе:
ΔТзам = Т10 - Т1 =Ккрm2 = Ккр (g2×1000)/(g2×М2)
Ккр − криоскопическая постоянная растворителя

Растворы электролитов дают большее понижение температуры замерзания вследствие диссоциации растворенного вещества на ионы; учитывает это явление изотонический коэффициент (i > 1)
ΔТзам=Т10 -Т1=iКкрm2=Ккр(g2×1000)(g2×М2)
Криоскопия − метод исследования растворов, в основе которого лежит измерение понижения температуры замерзания раствора по сравнению с температурой замерзания чистого растворителя.
Повышение температуры кипения Ткип примерно на порядок меньше, чем понижение температуры замерзания Ткзм, поэтому для определения моляр-ной массы растворенного вещества М2 используют последнее уравнение.

Осмотическое давление. Коллигативные свойства
Рассмотрим бинарный предельно разбавленный раствор. Пусть два образца этого раствора α и β, отличающиеся друг от друга концентрациями компо-нентов, разделены полунепроницаемой перегород-кой, которая пропускает молекулы растворителя и не пропускает молекулы растворенного вещества.
Пусть температура и давление по обе
стороны перегородки одинаковы. Если
концентрация растворителя в растворе α больше, чем в растворе β, то будет происходить перенос растворителя от раствора α к раствору β.
α
β

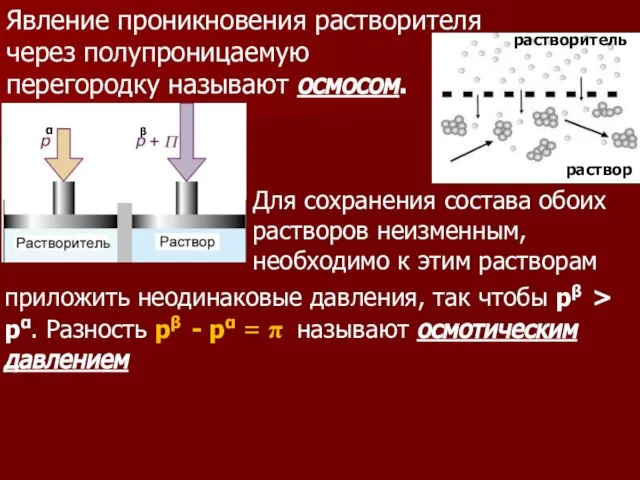
Явление проникновения растворителя
через полупроницаемую
перегородку называют осмосом.
растворитель
раствор
Для сохранения состава обоих растворов неизменным, необходимо к этим растворам
приложить неодинаковые давления, так чтобы рβ > рα. Разность рβ - рα = π называют осмотическим давлением
α
β

Вант-Гофф, показал, что
осмотическое давление равно тому давлению, которое производило бы растворенное вещество, если бы оно в виде газа занимало тот же объем, что и раствор π = n2RT/V = C2RT
π − осмотическое давление, атм.;
n2 − число молей растворенного вещества;
С2 − молярная концентрация растворенного вещества, моль/л;
Т − абсолютная температура, K; R − универсальная газовая, независящая от природы растворителя и растворенного вещества.

Осмотическое давление играет большую роль в биологических процессах, определяя распределение растворенных веществ и воды в тканях. В живых организмах есть полупроницаемые перегородки − мембраны - оболочки клеток.
Если поместить клетки в дистиллированную воду, они набухают, затем оболочки разрываются − лизис.
Если эритроциты поместить в воду, то они окрасят ее в красный цвет − гемолиз.
В растворах с высокой концентрацией солей, происходит сморщивание клеток из-за потери воды − плазмолиз.

Осмотическое давление - главная действующая сила, обеспечивающая движение воды в растениях и ее подъем от корней до вершины.
Т.о., осмотическое давление, понижение температуры замерзания, повышение температуры кипения растворителя в присутствии малых количеств растворенных веществ пропорционально мольной доле растворенного вещества, поэтому их называют коллигативными (зависящими от количества молей) свойствами растворов.

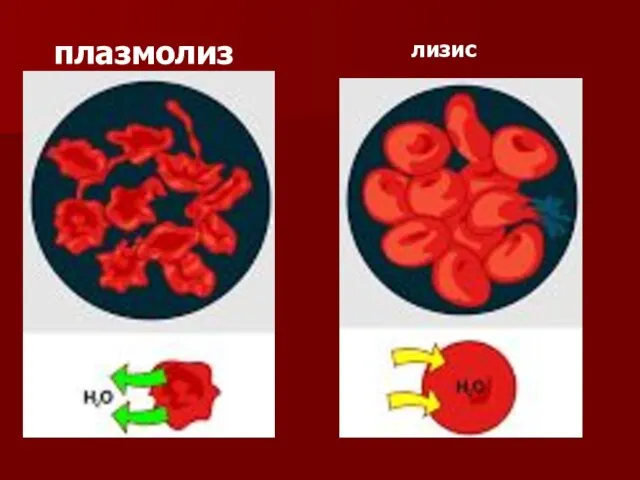
плазмолиз
лизис

Химическая кинетика и основные понятия
Химическая термодинамика указывает на принци-пиальную возможность протекания химической реак-ции в заданных условиях, рассматривая начальное и конечное состояние системы, а развитие реакции во времени (ее скорость и механизм) не исследует.
Раздел химии, изучающий скорости и механизмы реакций, называют химической кинетикой. Необходимость учета кинетических факторов дока-жем реакция синтеза NH3 из простых веществ N2(г) + 3H2(г) → 2NH3(г) ΔGo298 = -16,48 кДж/моль
С точки зрения термодинамики осуществима в стандартных, но не реализуется на практике из-за очень малой скорости процесса

Химические реакции осуществляют тремя способами:
1. Динамический способ проводят в реакторе идеального вытеснения, представляющем трубу, через которую движется элемент объема реакци-онной смеси Sdl (S – площадь поперечного сече-ния; dl – элементарная длина). Система – откры-тая, т.е. обменивается с окружающей средой массой.

В реакторе перемешивание отсутствует. Реакционная смесь непрерывно подается и не-прерывно выводится из нее, по истечении некоторого времени процесс становится стационарным, т.е. в каждой точке реактора сохраняется постоянство температуры и концентраций исхо-дных веществ и продуктов реакции во времени

3. Если в закрытый реактор с перемешиванием не-прерывно подавать исходные вещества и с той же скоростью отводить из него продукты, то система становится открытой. Метод проведения реакции - проточно-циркулярный
Скорость химической реакции характеризует интенсивность протекания процесса. Она обозначается буквой W.
Скорость реакции − число химических превращений в единицу времени в единице реакционного пространства. Для гомогенных процессов реакционное пространство – это объем реактора (V), для гетeрогенных - площадь поверхности границы раздела фаз S.

Элементарные химические реакции.
Закон действующих масс
Элементарная − химическая реакция, протекаю-щая в одну стадию (элементарный акт).
Большинство химических реакций – сложные. В сложных химических реакциях есть исходное вещество Аi и продукт А’i, образуются и расходуются промежуточные продукты А*i
Механизм сложной реакции - совокупность нескольких отличающихся друг от друга элементарных стадий и промежуточных веществ.
Реакции делят на обратимые и необратимые, которые идут в одном направлении до практически полного расходования хотя бы одного из реагентов.

* - из расчета по курсу 27 руб/долл.