Физическая химия, термодинамика

ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА
Изучает тепловые эффекты реакций, химические и фазовые равновесия.
Термины:
1) Термодинамическая система: тело или группа тел, обособленных от среды.
2) изолированная система - лишенная возможности обмена веществом и энергией со средой и имеющая постоянный объем.
3) равновесная система - в которой температура, давление, потенциал и другие параметры системы самопроизвольно не изменяются во времени и имеют одинаковое значение во всех точках системы.
4) функция состояния - величина, характеризующая состояние находящейся в равновесии системы, не зависящая от пути перехода в данное состояние.

Простые функции состояния (параметры состояния) - Т, Р, V.
Важнейшая функция состояния - внутренняя энергия U. Она характеризует общий запас энергии системы, кроме потенциальной и кинетической энергий системы как целого. Абсолютное значение не известно, так как не знаем всех видов энергии. Для химии достаточно знать относительные значения, так как главная задача - изучать изменения энергии при различных процессах .
5) термодинамический процесс - любое изменение в системе, сопровождающееся изменением хотя бы одной функции состояния.
Бесконечно малое изменение dX, конечное ΔX = X2 -X1.
Теплота (q) и работа (А) - не функции состояния, это формы передачи энергии среде посредством неупорядоченного (q) или упорядоченного (А) движения частиц.
q положительна, если поглощается системой, А положительна, если система совершает работу над средой.

Первое начало термодинамики:
приращение U системы равно количеству поглощенного тепла минус работа, совершаемая системой над средой:
ΔU=q-A или q = ΔU + А.
Суть этого закона понять довольно просто, ведь изменить внутреннюю энергию газа можно двумя способами: либо заставить его совершить работу или совершить над ним работу, либо передать ему некоторое количество теплоты или отвести от него некоторое количество теплоты.
Пример использования первого начала: заряженный аккумулятор может отдать энергию среде в виде работы или тепла.
Следствие: в изолированной системе U постоянна. U, A, q измеряются в Дж/моль.
Работу подразделяют на "полезную" и работу расширения против сил внешнего давления: dA=dAпол+PdV.
Пример: при растворении цинка в кислоте выделяется водород, который может вытолкнуть поршень из цилиндра.

Первое начало термодинамики (первый закон) имеет огромное значение в этой науке. Вообще понятие внутренней энергии вывело теоретическую физику 19 века на принципиально новый уровень. Появились такие понятия как термодинамическая система, термодинамическое равновесие, энтропия, энтальпия. Кроме того, появилась возможность количественного определения внутренней энергии и её изменения, что в итоге привело учёных к пониманию самой природы теплоты, как формы энергии. Ну, а если говорить о применении первого закона термодинамики в каких-либо задачах, то для этого необходимо знать два важных факта. Во-первых, внутренняя энергия идеального одноатомного газа равна кинетической энергии атомов, т.е. 3/2 кТ: а во-вторых, работа газа численно равна площади фигуры под графиком данного процесса, изображённого в координатах p—V. Учитывая это, можно вычислять изменение внутренней энергии, полученное или отданное газом количество теплоты и работу, совершённую газом или над газом в любом процессе. Можно также определять коэффициент полезного действия двигателя, зная какие процессы в нём происходят.

Тепловой эффект реакции (ТЭР) Q
Т.Э.Р. называется количество тепла, выделяемой в результате химической реакции при постоянной Т и отсутствии полезной работы.
Обозначается большой буквой Q. Два важных случая:
1) V,T=const (изохорно-изотермический), 2) P,T=const (изобарно-изотермический).
Рассмотрим первый случай. Из 1 начала ТД:
Qv=ΔU.
Значит, тепловой эффект реакции не зависит от пути перехода (закон Гесса) и может быть рассчитан через U.
Во втором случае
Qp= ΔU+PΔV.
Введем новую функцию Н - энтальпию: Н=U+PV. Это тоже функция состояния. Очевидно, Qp=ΔH, то есть тепловой эффект можно рассчитать по изменению H или U при переходе из одного состояния в другое, независимо от пути перехода. Это открывает возможность расчетов через вспомогательные промежуточные состояния.

В первом варианте выбираем набор простых веществ. Простое вещество - наиболее устойчивая форма существования данного химического элемента при стандартных условиях (1 атм и 2980К). Стандартной теплотой образования вещества называется тепловой эффект химической реакции образования 1 моля данного вещества из простых веществ при стандартных условиях (ΔfH0).
Теперь можно рассчитать тепловой эффект любой реакции, если известны теплоты образования всех участников реакции (первое следствие закона Гесса):
ΔH0=Σ(νiΔfH0)i) -Σ(νj ΔfH0 )j)

Второе следствие закона Гесса позволяет рассчитать тепловой эффект через cтандартные теплоты сгорания веществ, ΔсгHi. Это тепловой эффект реакции 1 моля данного вещества с кислородом с образованием высших оксидов при cтандартных условиях. Тогда:
ΔH0=Σ(νj (ΔсгH)j) -Σνi (ΔсгH)i
Для того, чтобы рассчитать тепловой эффект при любой температуре, надо ввести теплоемкость. Теплоемкость - отношение бесконечно малого количества поглощенного системой тепла к изменению температуры, которое этим вызывается, (при отсутствии полезной работы):
С=dq/dT

Рассмотрим условие постоянного объема:
Сv=dq/dT=dU/dT (т.к. PdV=0).
При Р=const :
Cp=dq/dT=(dU+PdV)/dT=dH/dT
Из этих формул можно найти температурную зависимость U или Н.
∫dH= ∫ CpdT.
Если в рассматриваемом интервале температур имеют место фазовые переходы "твердое тело – жидкость", "жидкость – пар", то в уравнениях температурной зависимости теплового эффекта появляются дополнительные составляющие, учитывающие тепловые эффекты фазовых переходов.

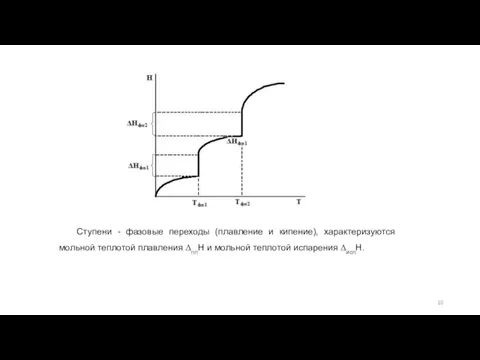
Ступени - фазовые переходы (плавление и кипение), характеризуются мольной теплотой плавления ΔплH и мольной теплотой испарения ΔиспH.

Зависимость теплового эффекта от температуры
Тепловой эффект процесса слабо зависит от давления и может существенно изменяться с температурой.
Рассмотрим тепловой эффект изобарной реакции и возьмем производную по температуре:
d(ΔH)/dT=dH2/dT-dH1/dT=Cp,2-Cp1=ΔCp
Температурный коэффициент теплового эффекта реакции равен приращению теплоемкости системы в результате реакции. Это закон Кирхгоффа в дифференциальной форме. Он позволяет рассчитать тепловой эффект реакции при нестандартной температуре.
d(ΔH)= ΔCpdT

Интегрируя уравнения Кирхгофа и , получим
выражения для расчета тепловых эффектов реакций при произвольных температурах:
V = const:
Р = const:
интегральная форма закона Кирхгофа
где , – тепловые эффекты, осуществляемые в стандартных условиях при V,Р = const, которые рассчитываются по закону Гесса с использованием стандартных теплот образования веществ.
Часто при проведении расчетов возникает необходимость учета температурной зависимости теплоемкости компонентов реакции.
Как правило, аналитическая форма функциональной зависимости C = f(T)неизвестна!

Теплоемкость вещества Cp можно представить в виде ряда:
Ср=а+bT+cT2 (органические вещества)
или Ср=а+bT+cT-1 (неорганические вещества).
Теперь изменение теплоемкости в ходе реакции можно представить в виде:
ΔСp = Δа+ΔbT+ΔcT-1
где Δа = Σ(νiΔai) - Σ(νj Δaj) и также для b и с.
Подстановка в интегральное уравнение Кирхгофа дает:
ΔHT=ΔH0+Δa(T-298)+Δb/2(T2-2982)-Δc(1/T-1/298) (неорганика)
и
ΔHT=ΔH0+Δa(T-298)+Δb/2(T2-2982)+Δc/3(T3-2983) (органика)
Тепловой эффект реакции сравнительно слабо зависит от температуры!

Второе начало термодинамики
Многие процессы не противоречат первому началу термодинамики, но не идут. Например, можно нагреть проволоку, замкнув контакты аккумулятора, но нельзя зарядить аккумулятор, нагревая проволоку.
2-е начало позволяет предсказывать возможность, направление и предел протекания процессов.
Новые термины:
1)процессы разделяются на самопроизвольные и несамопроизвольные. Самопроизвольный процесс проходит без направленных воздействий на систему, т.е. без совершения работы над системой. Наоборот, система в ходе этого процесса может совершить работу против внешних сил. В ходе самопроизвольного процесса система приближается к равновесию. Примеры: перенос тепла к холодному телу, диффузия, нейтрализация кислот основаниями, горение, коррозия. В изолированной системе протекают только самопроизвольные процессы.
Обратные процессы удаляли бы систему от равновесия и самопроизвольно не идут.

Попытки найти такой критерий привели к предположению, что самопроизвольно осуществляются только экзотермические процессы. Однако, мы знаем, что многие спонтанные термодинамические процессы, в частности химические реакции, могут протекать как с поглощением теплоты
так и с ее выделение:
сопровождаясь возрастанием неупорядоченности систем (газ более разупорядочен, чем кристалл или жидкость).

2). Равновесный процесс - протекающий через непрерывный ряд равновесных состояний, бесконечно медленный.
3) Обратимый процесс - протекающий в прямом, а затем обратном направлении так, что система и cреда возвращаются в исходные состояния. Обратимые процессы равновесные, и наоборот.
Реальные процессы не могут быть лишь приближенно обратимыми и равновесными.

Когда система поглощает тепло, ей сообщается дополнительная энергия в форме неупорядоченного теплового движения молекул. Увеличивается неупорядоченность системы, количественная мера неупорядоченности - энтропия.
Клаузиусом была введена функция, названная энтропией S, и сформулировано два принципа: принцип существования энтропии и принцип возрастания энтропии в изолированных системах.
Принцип существования энтропии
Для каждой термодинамической системы существует функция состояния системы S - энтропия, определяемая тем, что ее дифференциал (dS) при элементарном обратимом (равновесном) процессе равен отношению бесконечно малого количества теплоты (δq), сообщенного системе, к абсолютной температуре системы:
dS=δq/T

Принцип возрастания энтропии
Энтропия изолированной системы при наличии в ней необратимых процессов всегда возрастает
Таким образом, в изолированной системе обратимые процессы протекают без изменения энтропии, а необратимые - с возрастанием энтропии

Свойства энтропии
Энтропия– функция состояния системы. Ее изменение зависит от начального и конечного состояний системы.
Энтропия является мерой неупорядоченности системы.
Энтропия – аддитивная функция, т.е. энтропия системы равна сумме энтропий ее частей (это экстенсивный параметр!)
Энтропия– вероятностная функция. Она показывает вероятность процесса и направление наиболее его вероятного протекания.
Энтропия – мера рассеивания энергии в окружающую среду, т.е. та часть энергии, которая в полезную работу не превращается!!!