Использование комбинаторных задач для подсчета вероятностей

Решить уравнение

ПРИМЕР 1
Из колоды в 36 карт случайным образом вытаскивают три карты.
Какова вероятность того, что среди них:
нет пиковой дамы?

ПРИМЕР 1
нет пиковой дамы?
У нас имеется множество из 36 элементов – игральных карт. Мы производим выбор трех элементов, порядок выбора не важен. Значит имеется
исходов.

ПРИМЕР 1
нет пиковой дамы?
Среди всех исходов нам надо сосчитать те, в которых нет пиковой дамы (событие А). Поэтому отложим даму пик в сторону и будем выбирать 3 карты из оставшихся 35 карт. Получаются все интересующие нас варианты:

Осталось вычислить нужную вероятность:

ПРИМЕР 1
Из колоды в 36 карт случайным образом вытаскивают три карты.
Какова вероятность того, что среди них:
есть пиковая дама?

ПРИМЕР 1
есть пиковая дама?

ПРИМЕР 2
В урне лежит 10 белых и 11 черных шаров. Случайным образом достают 5 шаров. Какова вероятность того, что среди этих 5 шаров ровно 3 белых?

Шары в урне не различимы на ощупь. Из 21 шара случайным образом выбирают 5 шаров. Порядок не важен. Значит, существует
таких выборов.

3 - белые, 2 - черные.
Из 10 белых – 3
способами
Из 11 черных – 2
способами
По правилу умножения

Значит,

ПРИМЕР 2
В урне лежит 10 белых и 11 черных шаров. Случайным образом достают 5 шаров. Какова вероятность того, что среди этих 5 шаров не менее 4 белых шаров?

В – событие, состоящее в том, что белых шаров ровно 4, а С – событие, состоящее в том, что все 5 шаров белые.

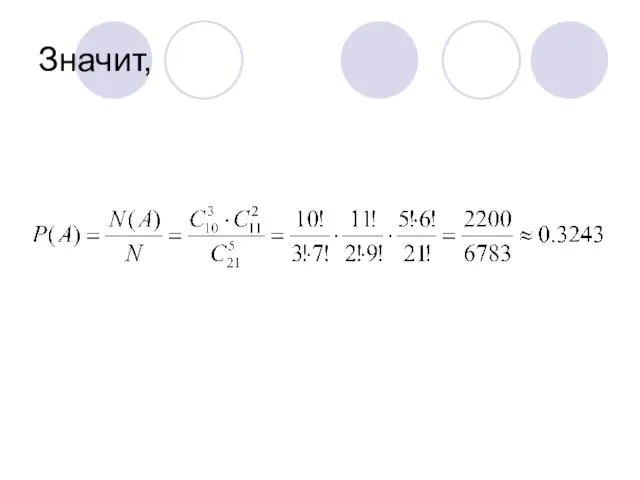
События В и С не могут наступить одновременно, т.е. они несовместимы. Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий.
Значит,
P(B+C)=P(B)+P(C)=0.1135+0.0124=0.1259

ПРИМЕР 2
В урне лежит 10 белых и 11 черных шаров. Случайным образом достают 5 шаров. Какова вероятность того, что большинство шаров - белые?

Интересующее нас событие произойдет в следующих случаях:
Из 5 шаров – 4 белых и 1 черный;
3 белых и 2 черных;
Все 5 шаров белые.
События не могут наступить одновременно.
P(A+B+C)=P(A)+P(B)+P(C)=0.3243+ +0.1135+0.0124=0.4502

Дополнительные задачи

№1
Сколько четырехбуквенных слов можно образовать из букв слова САПФИР?

Порядок важен

№1
Сколько четырехбуквенных слов можно образовать из букв слова САПФИР, таких, которые не содержат буквы Р?

№1
Сколько четырехбуквенных слов можно образовать из букв слова САПФИР, таких, которые начинаются с буквы С и оканчиваются буквой Р?

На 1 место – С – одним способом
На последнее – Р – одним способом
Остаются 4 буквы, которые размещаем по 2 местам.

№2
Сколько пятибуквенных слов, каждое из которых состоит из 3 согласных и 2 гласных, можно образовать из слова УРАВНЕНИЕ?
Решить с использованием треугольника Паскаля.