Содержание
- 2. Системы счисления § 9. Системы счисления
- 3. Вспомним известное… Система счисления — это правила записи чисел с помощью специальных знаков — цифр, а
- 4. Формы записи чисел 6 3 7 5 3 2 1 0 разряды 5 70 300 =
- 5. Перевод в десятичную систему a3a2a1a0 = a3⋅p 3 + a2⋅p 2 + a1⋅p 1 + a0⋅p
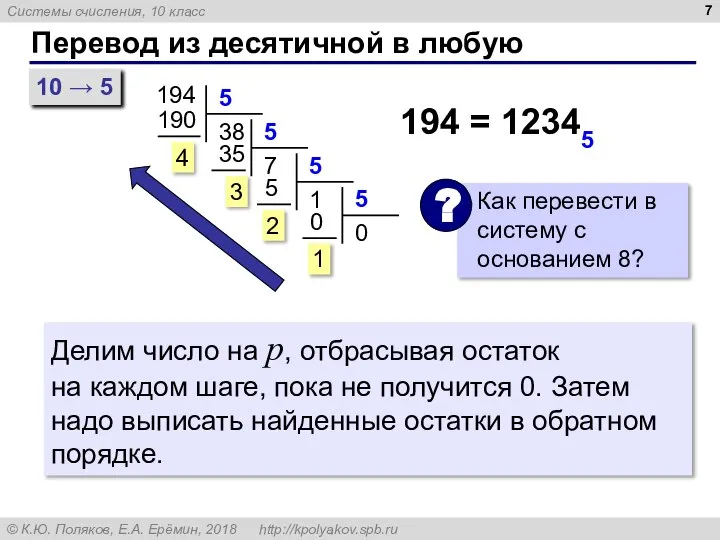
- 6. Перевод из десятичной в любую 194 = 12345 = ((1⋅5 + 2)⋅5 + 3)⋅5 + 4
- 7. Перевод из десятичной в любую 194 194 = 12345 10 → 5 Делим число на p,
- 8. в записи есть цифра 6, поэтому X > 6 переводим правую часть в десятичную систему решаем
- 9. в записи есть цифра 5, поэтому X > 5 переводим правую часть в десятичную систему решаем
- 10. Задачи Задача: найдите все основания систем счисления, в которых запись десятичного числа 24 оканчивается на 3.
- 11. Задачи Задача: найдите все десятичные числа, не превосходящие 40, запись которых в системе счисления с основанием
- 12. Задачи Задача: Все 5-буквенные слова, составленные из букв А, О и У, записаны в алфавитном порядке.
- 13. Задачи Задача: Значение арифметического выражения 92017 + 32015 – 9 записали в системе счисления с основанием
- 14. Задачи Задача: Значение арифметического выражения 92017 + 32015 – 9 записали в системе счисления с основанием
- 15. Дробные числа 0,6375 = 6·0,1 + 3·0,01 + 7·0,001 + 5·0,0001 0, 6 3 7 5
- 16. Дробные числа: из десятичной в любую 0,12345 = 5-1·(1 + 5-1·(2 + 5-1·(3 + 5-1·4))) 5·(0,12345)=
- 17. Дробные числа: из десятичной в любую 10 → 5 0,9376 0,9376 = 0,43215 10 → 5
- 18. Дробные числа: из десятичной в любую 10 → 6 25,375 = 25 + 0,375
- 19. Системы счисления § 11. Двоичная система счисления
- 20. Двоичная система Основание (количество цифр): 2 Алфавит: 0, 1 10 → 2 2 → 10 19
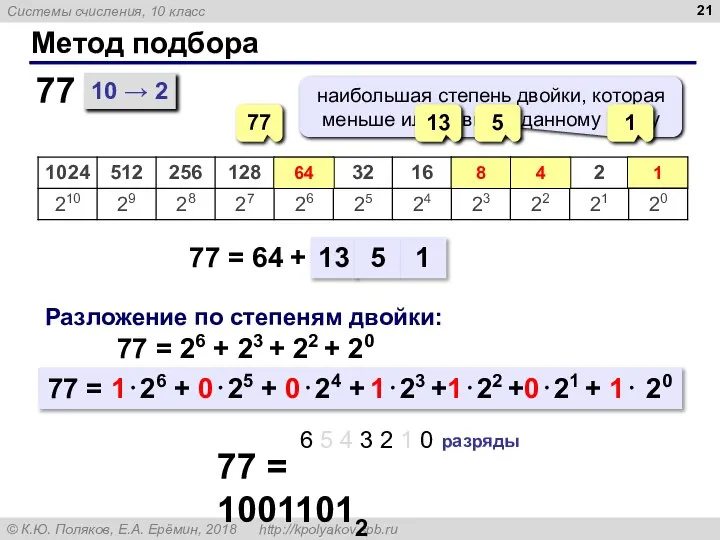
- 21. Метод подбора 10 → 2 77 = 64 + 77 77 64 Разложение по степеням двойки:
- 22. Перевод из двоичной в десятичную 10011012 = 26 + 23 + 22 + 20 6 5
- 23. Арифметические операции сложение вычитание 0+0=0 0+1=1 1+0=1 1+1=102 1 + 1 + 1 = 112 0-0=0
- 24. Арифметические операции
- 25. Арифметические операции
- 26. Арифметические операции умножение деление 1 0 1 0 12 × 1 0 12 1 0 1
- 27. Работа со степенями числа 2 Задача: Запишите значение выражения 212 + 27 – 25 в системе
- 28. Работа со степенями числа 2 Задача: Запишите значение выражения 212 + 27 – 25– 23 в
- 29. Работа со степенями числа 2 Задача: Сколько единиц и значащих нулей в двоичной записи числа 8128
- 30. Дробные числа 10 → 2 0,8125 0,8125 = 0,11012 10 → 2 0,6 = 0,100110011001… =
- 31. Дробные числа Большинство дробных чисел хранится в памяти с некоторой погрешностью. При выполнении вычислений с дробными
- 32. Двоичная система счисления длинная запись чисел: 1024 = 100000000002 запись однородна (только 0 и 1) нужны
- 33. Системы счисления § 12. Восьмеричная система счисления
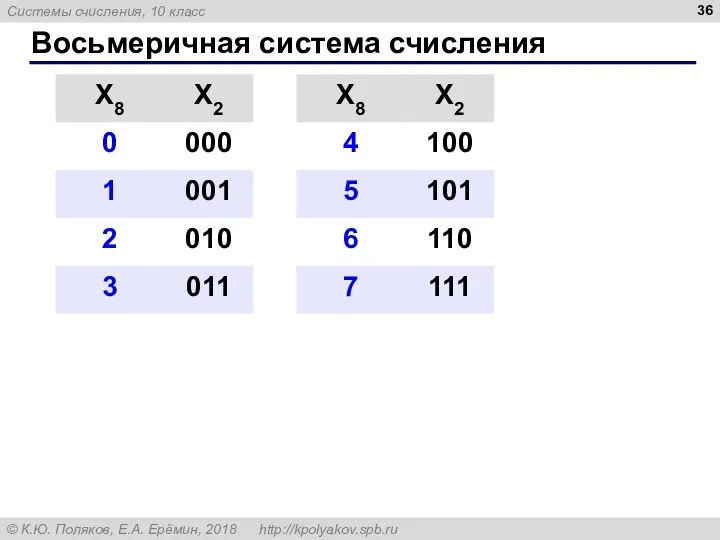
- 34. Восьмеричная система счисления Основание: 8 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7 10 →
- 35. Примеры 134 = 75 = 1348 = 758 =
- 36. Восьмеричная система счисления
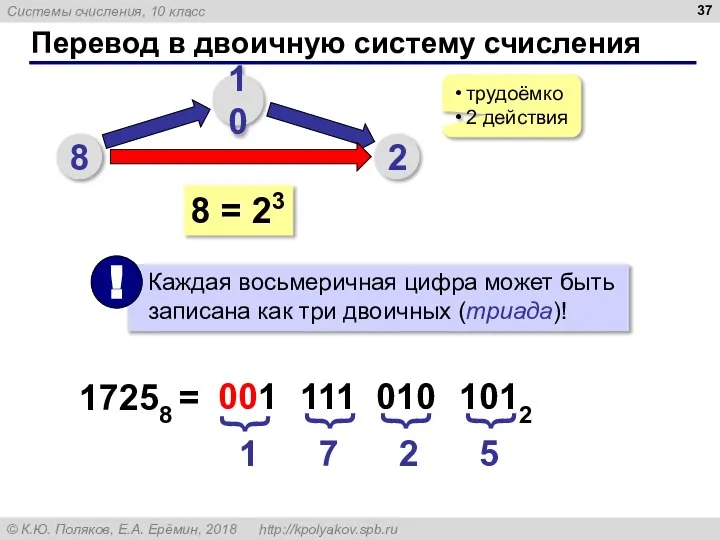
- 37. Перевод в двоичную систему счисления 8 10 2 трудоёмко 2 действия 8 = 23 17258 =
- 38. Примеры 34678 = 21488 = 73528 = 12318 =
- 39. Перевод из двоичной в восьмеричную 10010111011112 Шаг 1. Разбить на триады, начиная справа: 001 001 011
- 40. Примеры 1011010100102 = 111111010112 = 11010110102 =
- 41. Арифметические операции сложение 1 5 68 + 6 6 28 1 1 6 + 2 =
- 42. Примеры
- 43. Арифметические операции вычитание 4 5 68 – 2 7 78 ∙ (6 + 8) – 7
- 44. Примеры
- 45. Применение восьмеричной системы компактная запись данных в компьютерах 1960-х годов: 101001112 = 2478 запись команд компьютеров
- 46. Системы счисления § 13. Шестнадцатеричная система счисления
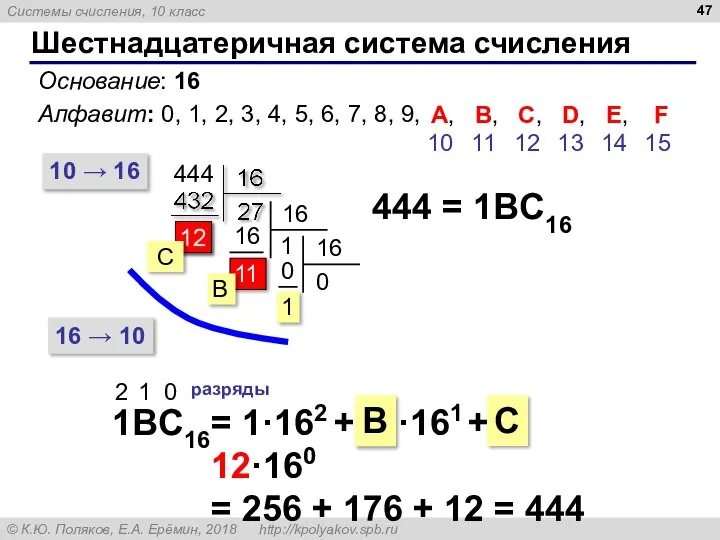
- 47. 11 Шестнадцатеричная система счисления Основание: 16 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8,
- 48. Примеры 171 = 206 = 1C516 = 22B16 =
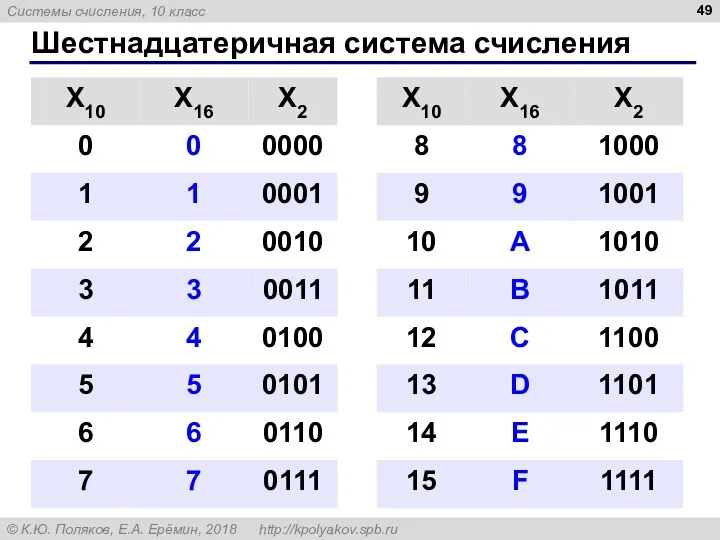
- 49. Шестнадцатеричная система счисления
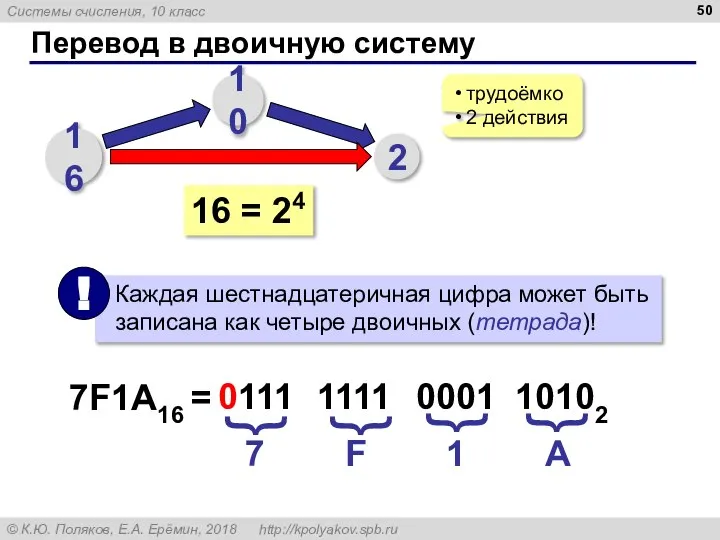
- 50. Перевод в двоичную систему 16 10 2 трудоёмко 2 действия 16 = 24 7F1A16 = 7
- 51. Примеры C73B16 = 2FE116 =
- 52. Перевод из двоичной системы Шаг 1. Разбить на тетрады, начиная справа: 0001 0010 1110 11112 Шаг
- 53. Примеры 10101011010101102 = 1111001101111101012 = 1101101101011111102 =
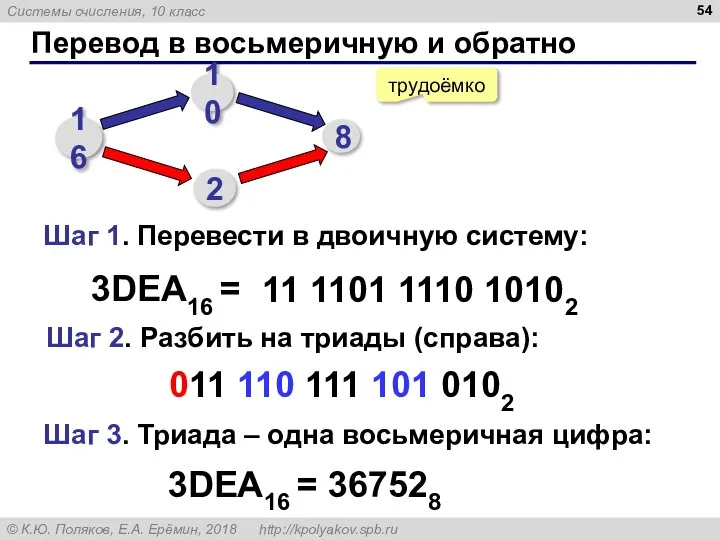
- 54. Перевод в восьмеричную и обратно трудоёмко 3DEA16 = 11 1101 1110 10102 16 10 8 2
- 55. Примеры A3516 = 7658 =
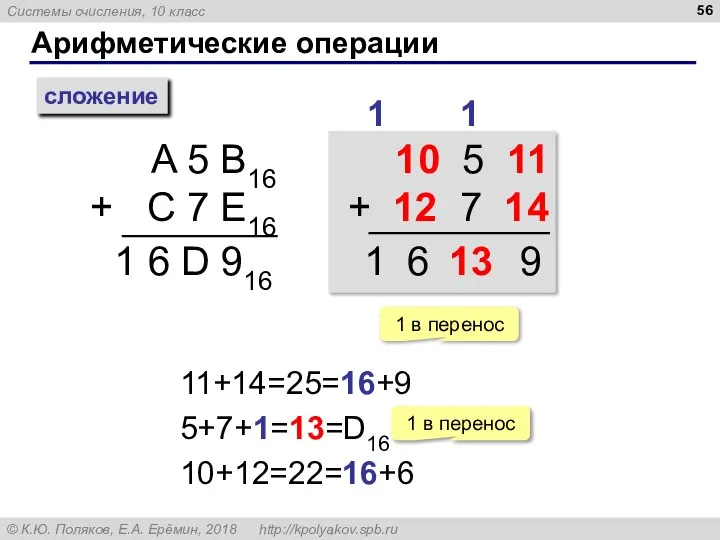
- 56. Арифметические операции сложение A 5 B16 + C 7 E16 1 1 6 D 916 10
- 57. Примеры С В А16 + A 5 916 F D В16 + A B C16
- 58. Арифметические операции вычитание С 5 B16 – A 7 E16 заём ∙ 1 D D16 12
- 59. Примеры 1 В А16 – A 5 916
- 60. Применение шестнадцатеричной системы компактная запись данных : запись команд компьютеров 5 E 5E16
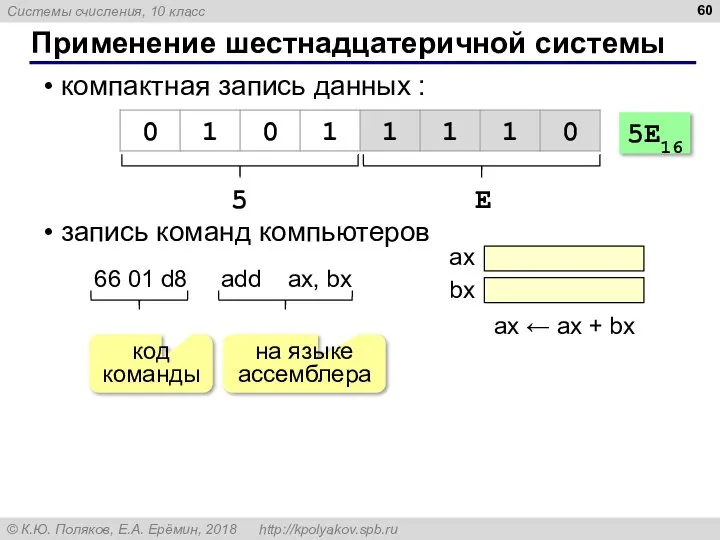
- 61. Системы счисления § 14. Другие системы счисления
- 62. Задача Баше о наборе гирь + 1 гиря на правой чашке 0 гиря снята – 1
- 63. Троичная уравновешенная система ЭВМ «Сетунь» (1958) , Н.П. Брусенцов Основание: 3 Алфавит: («-1»), 0, 1 Для
- 64. Двоично-десятичная система (ДДС) Десятичные цифры, закодированные в двоичном коде. Вinary coded decimal (BCD). 9024,19 = 1001
- 65. Конец фильма ПОЛЯКОВ Константин Юрьевич д.т.н., учитель информатики ГБОУ СОШ № 163, г. Санкт-Петербург [email protected] ЕРЕМИН
- 67. Скачать презентацию






















































 Структура действия и структуры данных
Структура действия и структуры данных GRandapp. Смартфон - это просто
GRandapp. Смартфон - это просто Медиатекст: дефиниция, основные свойства, типология
Медиатекст: дефиниция, основные свойства, типология Техника безопасности и правила поведения при работе в компьютерном классе
Техника безопасности и правила поведения при работе в компьютерном классе Есть, что сказать людям, но нет своего сайта?
Есть, что сказать людям, но нет своего сайта? Многоуровневая модель и протоколы
Многоуровневая модель и протоколы Команды перехода (1)
Команды перехода (1) Система управления автоматическими звонками
Система управления автоматическими звонками Кодирование текстовой и графической информации
Кодирование текстовой и графической информации Аппаратное обеспечение ПК
Аппаратное обеспечение ПК Основы программирования (Паскаль)
Основы программирования (Паскаль) Беспилотные автомобили — транспорт будущего. 8 класс
Беспилотные автомобили — транспорт будущего. 8 класс Разработка программного прикладного продукта Лаборант для ГБПОУ ИО БрПК
Разработка программного прикладного продукта Лаборант для ГБПОУ ИО БрПК Принцип временного разделения каналов. Система передачи
Принцип временного разделения каналов. Система передачи Навигационная система дополненной реальности в современных системах
Навигационная система дополненной реальности в современных системах Создание запросов. 11 класс
Создание запросов. 11 класс Система автоматизации договорной работы ТурбоКонтракт
Система автоматизации договорной работы ТурбоКонтракт Информатика, информация и её классификация
Информатика, информация и её классификация Программирование. Variadic Templates. LSP
Программирование. Variadic Templates. LSP Лайфхаки, упрощающие жизнь 1С-никам
Лайфхаки, упрощающие жизнь 1С-никам Использование интерактивных систем на курсах повышения квалификации по ИКТ
Использование интерактивных систем на курсах повышения квалификации по ИКТ php5mI1jg_Pervoe-znakomstvo-s-kompyuterom (1)
php5mI1jg_Pervoe-znakomstvo-s-kompyuterom (1) МДК 02.02. Web-программирование. Язык РНР Работа с файловой системой
МДК 02.02. Web-программирование. Язык РНР Работа с файловой системой Журнал ShowKids. Биография группы
Журнал ShowKids. Биография группы Образовательная 3D-модель, пазл Белгородская область
Образовательная 3D-модель, пазл Белгородская область Условные переменные
Условные переменные Домашнее (условие фано)
Домашнее (условие фано) Теоретические основы информатики. Аксиомы информатики
Теоретические основы информатики. Аксиомы информатики