Содержание
- 2. Логика, высказывания Логика (др.греч. λογικος) – это наука о том, как правильно рассуждать, делать выводы, доказывать
- 3. Высказывание или нет? Сейчас идет дождь. Жирафы летят на север. История – интересный предмет. У квадрата
- 4. Логика и компьютер Логика изучает операции между 0 и 1! Джордж Буль Алгебра логики — это
- 5. Простые и составные высказывания A – Сейчас идет дождь. B – Форточка открыта. простые высказывания (элементарные)
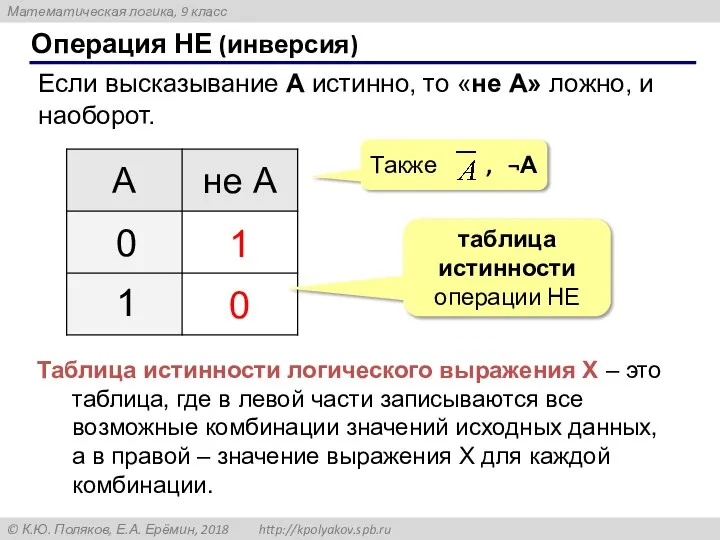
- 6. Операция НЕ (инверсия) Если высказывание A истинно, то «не А» ложно, и наоборот. 0 1 1
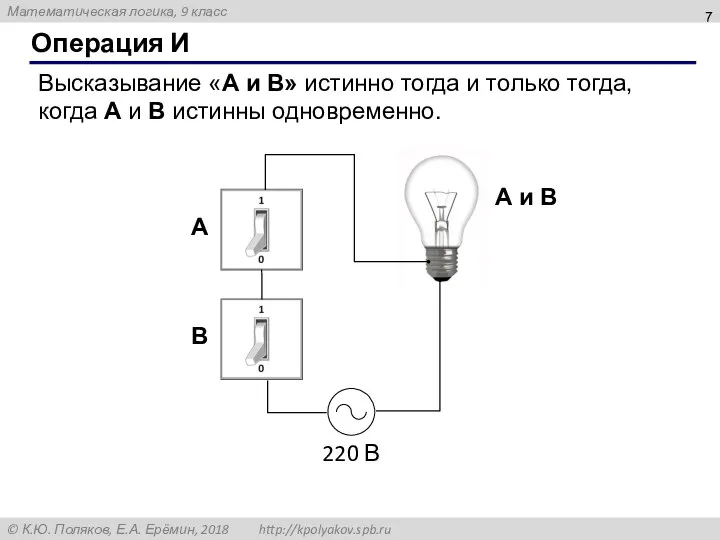
- 7. Операция И Высказывание «A и B» истинно тогда и только тогда, когда А и B истинны
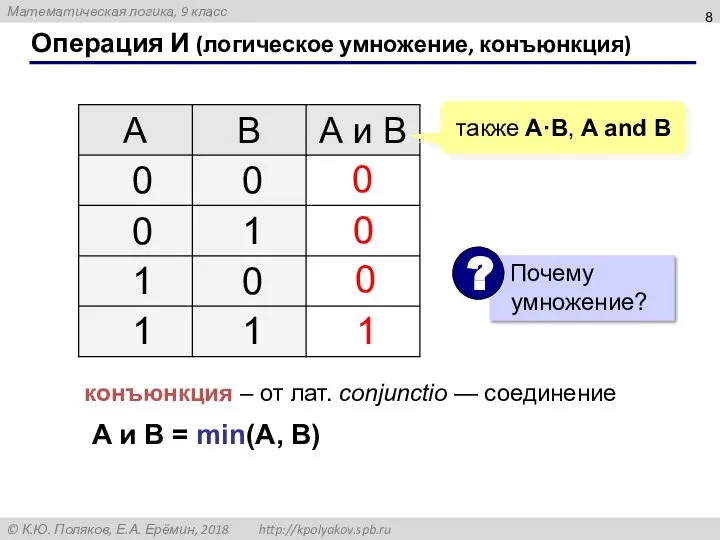
- 8. Операция И (логическое умножение, конъюнкция) 1 0 также A·B, A and B 0 0 конъюнкция –
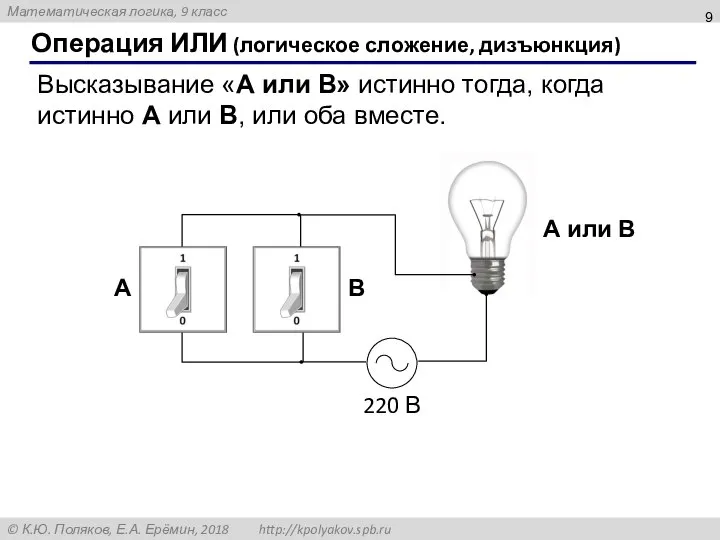
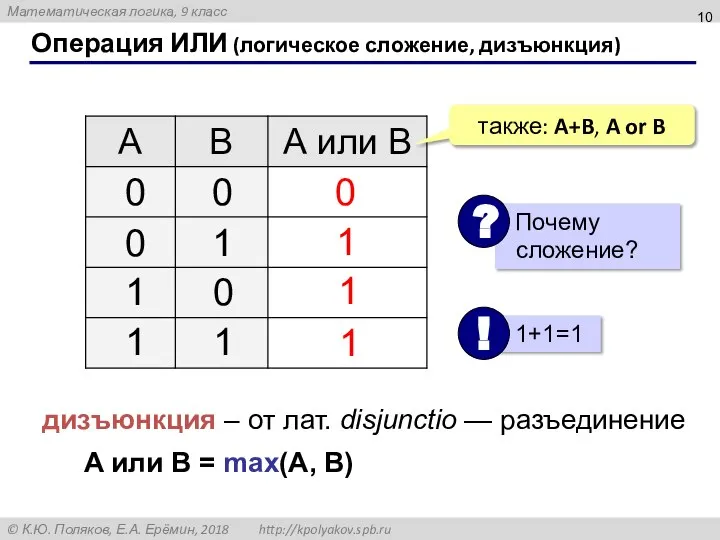
- 9. Операция ИЛИ (логическое сложение, дизъюнкция) Высказывание «A или B» истинно тогда, когда истинно А или B,
- 10. Операция ИЛИ (логическое сложение, дизъюнкция) 1 0 также: A+B, A or B 1 1 дизъюнкция –
- 11. Упрощение логических выражений A и 0 = A ∙ 0 = A и 1 = A
- 12. Логические выражения Логическое выражение — это выражение, результат вычисления которого — логическое значение (истина или ложь).
- 13. Порядок вычисления скобки НЕ И ИЛИ 1 2 3 4 5 6
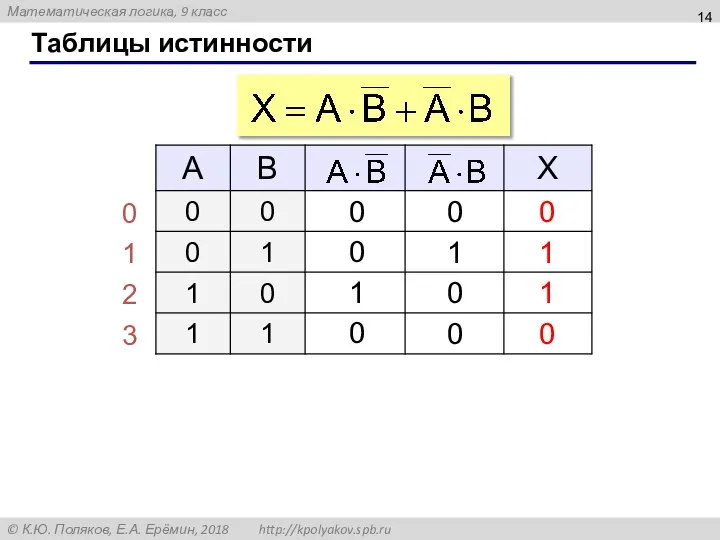
- 14. Таблицы истинности
- 16. Скачать презентацию







 1С- Битрикс. Структура bitrix framework, работа с административной панелью, редактирование меню
1С- Битрикс. Структура bitrix framework, работа с административной панелью, редактирование меню 50 главных категорий контента
50 главных категорий контента Системы счисления. Математические основы информатики
Системы счисления. Математические основы информатики Каналы Связи
Каналы Связи Оценка сайтов
Оценка сайтов Передача данных. МПСвЭПиТК
Передача данных. МПСвЭПиТК Ячейки памяти компьютера
Ячейки памяти компьютера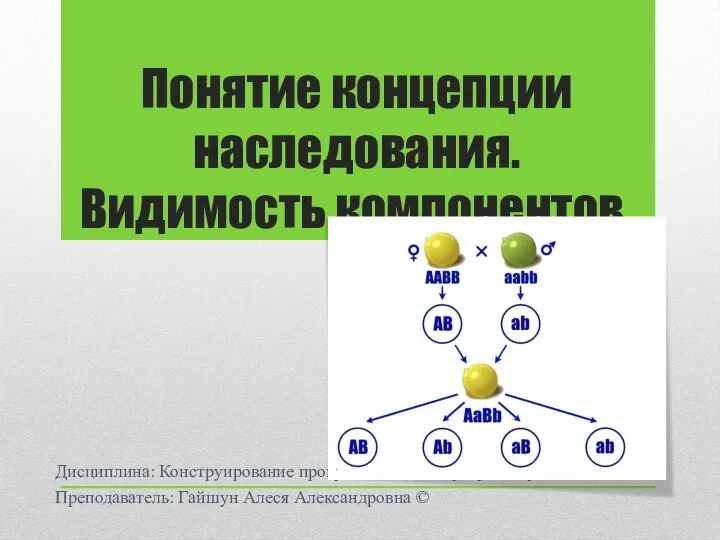 Понятие концепции наследования. Видимость компонентов
Понятие концепции наследования. Видимость компонентов Online-курсы Платформа Открытое образование
Online-курсы Платформа Открытое образование Индивидуальный проект. От абака до компьютера
Индивидуальный проект. От абака до компьютера Правила пользования компьютерной сетью ООО Гутцайт групп
Правила пользования компьютерной сетью ООО Гутцайт групп Аксиомы и определения доступа субъектов к объектам
Аксиомы и определения доступа субъектов к объектам Алгоритмизация и программирование
Алгоритмизация и программирование Кафедра информационной и технологической культуры
Кафедра информационной и технологической культуры Как с помощью продукции повседневного ухода за собой получить доход в интернете
Как с помощью продукции повседневного ухода за собой получить доход в интернете Поштові служби інтернету. Електронна скринька та електронне листування
Поштові служби інтернету. Електронна скринька та електронне листування Текстовая информация. Единицы измерения
Текстовая информация. Единицы измерения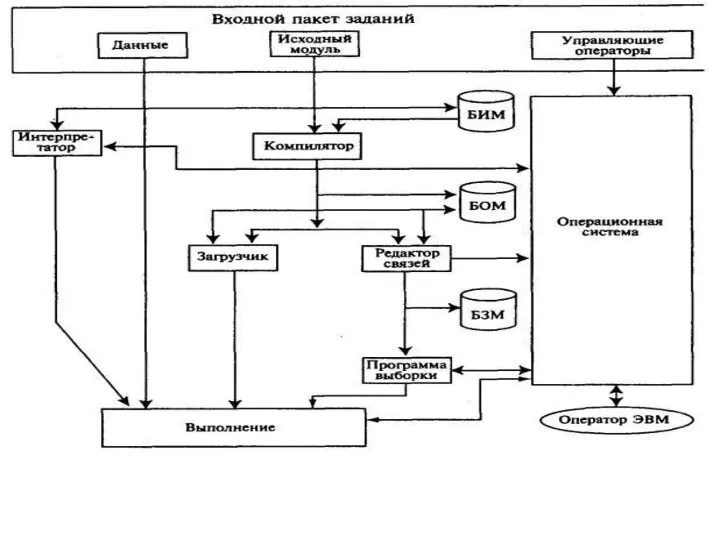 Входной пакет заданий
Входной пакет заданий Архитектура персонального компьютера
Архитектура персонального компьютера История интернета
История интернета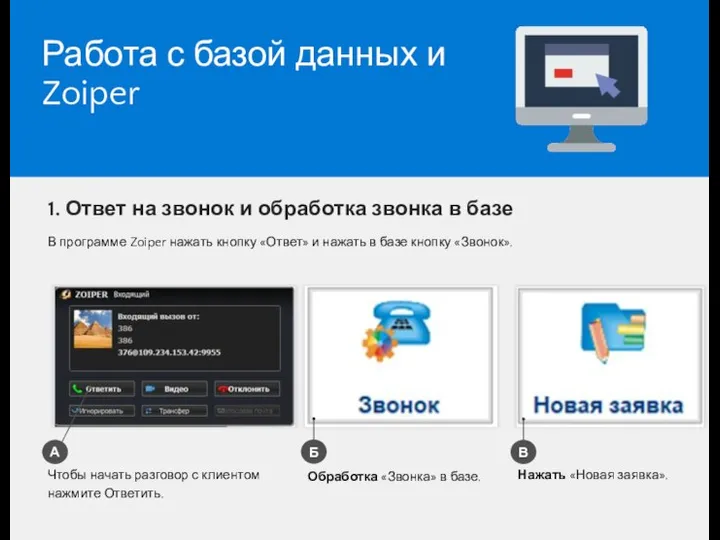 Работа с базой данных и Zoiper
Работа с базой данных и Zoiper Темная сторона цифрового мира. О массовой уязвимости процессоров Intel
Темная сторона цифрового мира. О массовой уязвимости процессоров Intel Основы программирования на языке Python. Школа::Кода (занятие 3)
Основы программирования на языке Python. Школа::Кода (занятие 3) Информация и ее свойства
Информация и ее свойства Проектирование структуры БД. Методические указания к курсовой работе Разработка и эксплуатация АИС Часть 1
Проектирование структуры БД. Методические указания к курсовой работе Разработка и эксплуатация АИС Часть 1 Программирование на языке C++
Программирование на языке C++ Компьютерные сети
Компьютерные сети Крестики-нолики. Шаблон
Крестики-нолики. Шаблон