Содержание
- 2. Приоритетная очередь (priority queue) Абстрактные типы данных
- 3. Приоритетная очередь (англ. priority queue) Предположим, что для каждого элемента определён некоторый приоритет. В простейшем случае
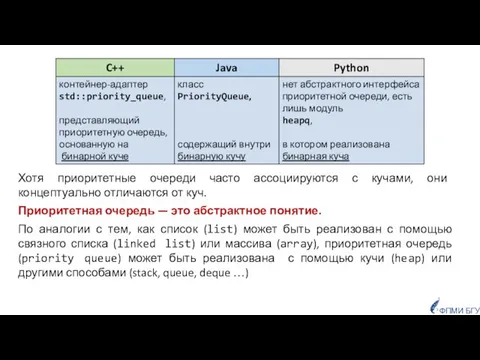
- 4. Хотя приоритетные очереди часто ассоциируются с кучами, они концептуально отличаются от куч. Приоритетная очередь — это
- 5. Бинарная куча (binary heap) Биномиальная куча (binomial heap) Куча Фибоначчи (Fibonacci heap ) Структуры данных
- 6. Куча (англ. heap) — специализированная древовидная структура данных, которая удовлетворяет свойству кучи. В вершинах древовидной структуры
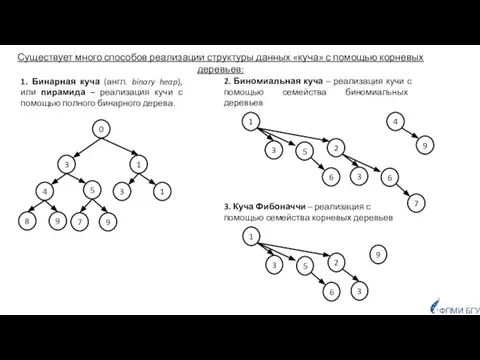
- 7. Существует много способов реализации структуры данных «куча» с помощью корневых деревьев: 1. Бинарная куча (англ. binary
- 8. GetMin() — поиск минимального ключа; IncreaseKey DecreaseKey — модификация ключа вершины на заданную величину (предполагается, что
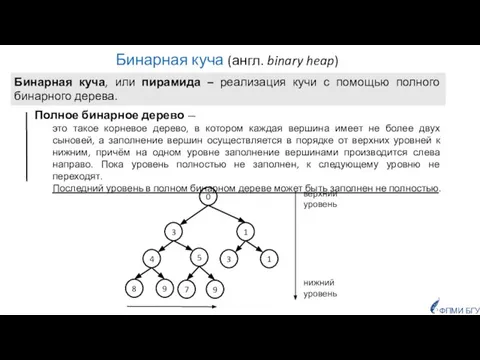
- 9. Бинарная куча (англ. binary heap) Полное бинарное дерево — это такое корневое дерево, в котором каждая
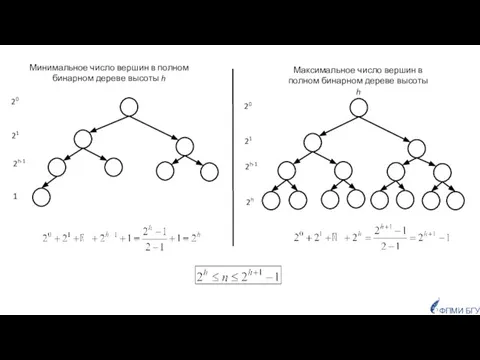
- 10. 20 21 20 21 Максимальное число вершин в полном бинарном дереве высоты h Минимальное число вершин
- 11. Высота h полного бинарного дерева, содержащего n вершин, — O(log n).
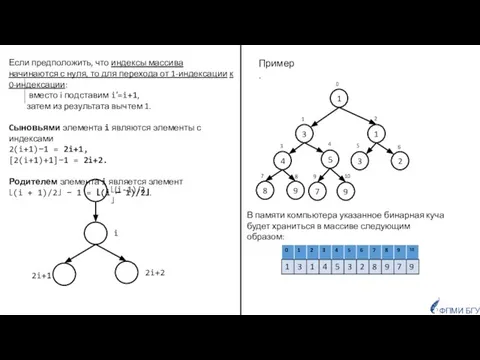
- 12. В памяти компьютера полное бинарное дерево легко реализуется с помощью массива. Если предположить, что индексы массива
- 13. В памяти компьютера указанное бинарная куча будет храниться в массиве следующим образом: Если предположить, что индексы
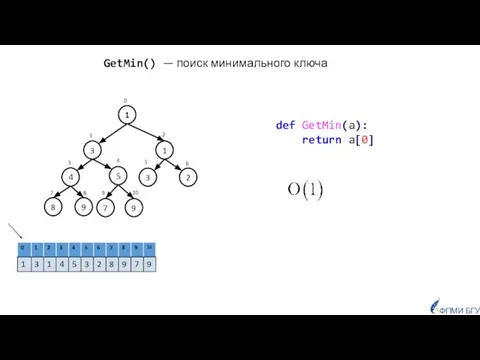
- 14. GetMin() — поиск минимального ключа 1 3 2 3 5 4 1 9 9 7 8
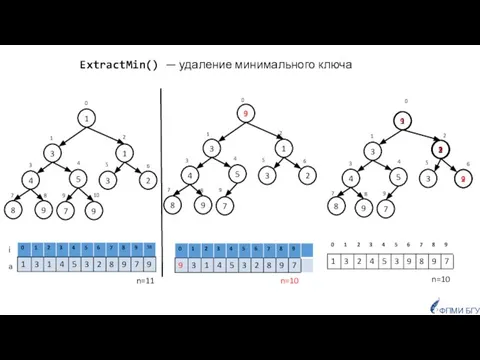
- 15. ExtractMin() — удаление минимального ключа 1 3 2 3 5 4 1 9 9 7 8
- 16. def ExtractMin(a): a[0] = a[len(a) - 1] a.pop() i = 0 while 2 * i +
- 17. ExtractMin() — удаление минимального ключа
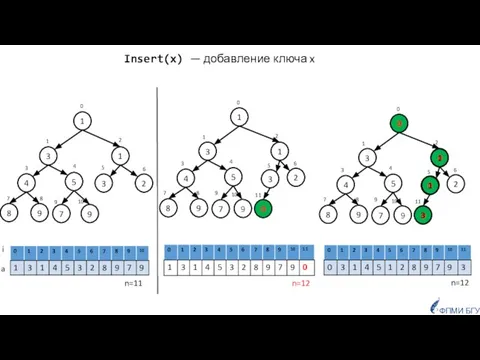
- 18. Insert(x) — добавление ключа x 1 3 2 3 5 4 1 9 9 7 8
- 19. def Insert(a, x): a.append(x) i = len(a) - 1 while i > 0: j = (i
- 20. Insert(x) — добавление ключа x
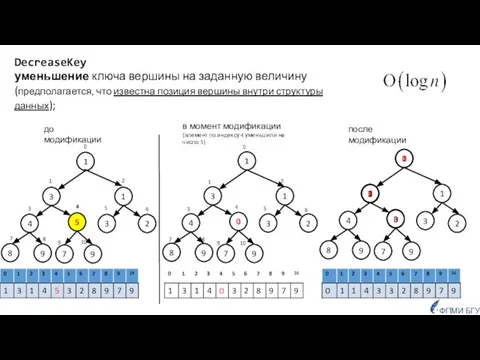
- 21. DecreaseKey уменьшение ключа вершины на заданную величину (предполагается, что известна позиция вершины внутри структуры данных); 1
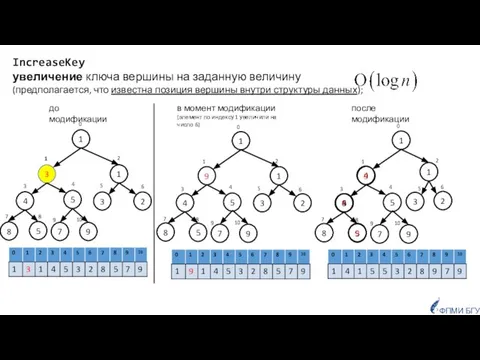
- 22. IncreaseKey увеличение ключа вершины на заданную величину (предполагается, что известна позиция вершины внутри структуры данных); 1
- 23. DecreaseKey уменьшение ключа вершины на заданную величину IncreaseKey увеличение ключа вершины на заданную величину предполагается, что
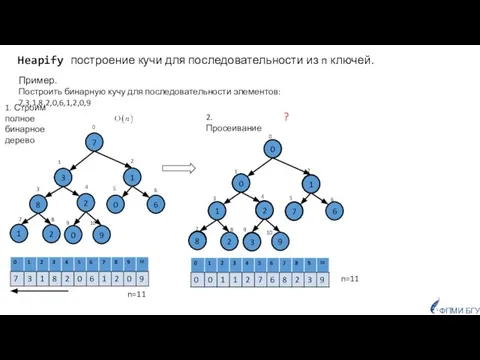
- 24. Heapify построение кучи для последовательности из n ключей. n=11 1. Строим полное бинарное дерево 1 3
- 25. Для того, чтобы оценить время работы построения бинарной кучи для последовательности из n элементов, необходимо оценить
- 26. Так как число вершин полного бинарного дерева высоты h удовлетворяет неравенствам: Получаем оценку сверху на число
- 27. Heapify построение кучи для последовательности из n ключей:
- 28. GetMin() поиск минимального ключа; IncreaseKey DecreaseKey модификация ключа вершины на заданную величину (предполагается, что известна позиция
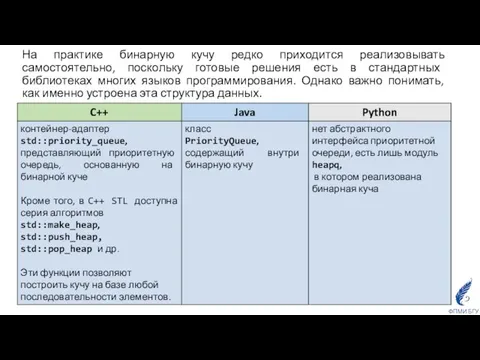
- 29. На практике бинарную кучу редко приходится реализовывать самостоятельно, поскольку готовые решения есть в стандартных библиотеках многих
- 30. Биномиальная куча B0 B1 B2 B3 Семейство биномиальных деревьев: у биномиального дерева высоты h на глубине
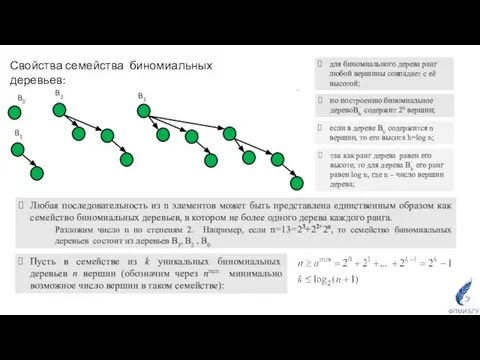
- 31. Свойства семейства биномиальных деревьев: по построению биномиальное деревоBh содержит 2h вершин; для биномиального дерева ранг любой
- 32. Дополнительные вспомогательные операции link и cut, которые нужны для выполнения базовых операций x y x y
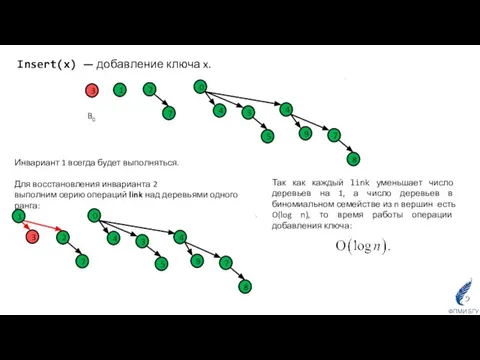
- 33. 1 0 4 3 5 4 9 7 8 2 7 Insert(x) — добавление ключа x.
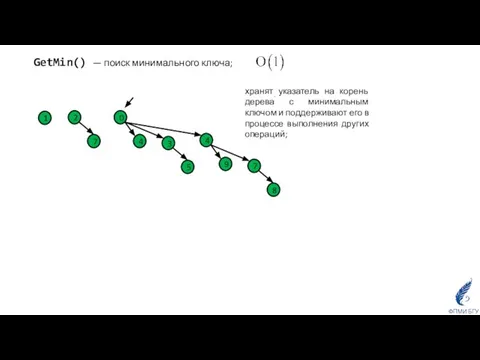
- 34. 1 0 4 3 5 4 9 7 8 2 7 GetMin() — поиск минимального ключа;
- 35. 1 0 4 3 5 4 9 7 8 2 7 ExtractMin() — удаление минимального ключа;
- 36. Heapify — построение кучи для последовательности из n ключей Биномиальную кучу будем строить вызовом n раз
- 37. то время работы алгоритма Heapify построения кучи для последовательности из n ключей в худшем случае есть
- 38. Предполагается, что задана позиция вершины внутри структуры данных. 0 4 3 5 2 9 7 8
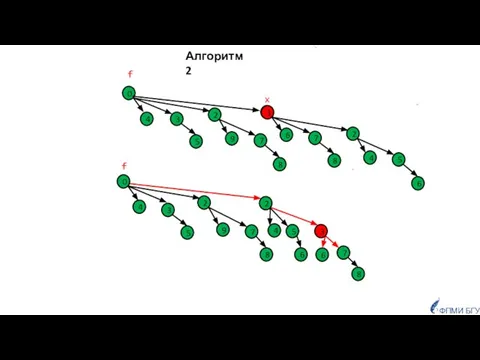
- 39. IncreaseKey(увеличение ключа) Увеличиваем ключ вершины x. Если после этого для x нарушается свойство кучи, то просеиваем
- 40. Увеличиваем ключ вершине x. Время работы алгоритма: Если инвариант 1 для x НЕ выполняется, то 3.1.
- 41. 0 4 3 5 2 9 7 8 1 6 7 8 2 4 5 6
- 42. GetMin() — поиск минимального ключа; IncreaseKey DecreaseKey — модификация ключа вершины на заданную величину (предполагается, что
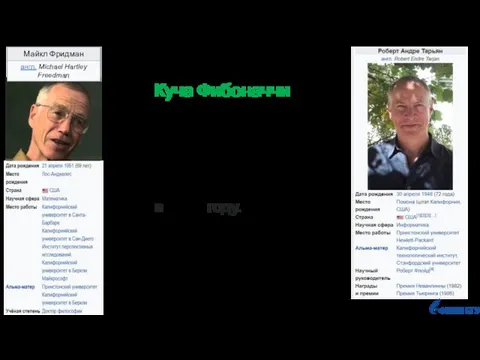
- 43. Куча Фибоначчи (Fibonacci heap) была предложена Майклом Фридманом и Робертом Тарьяном в 1984 году.
- 44. Куча Фибоначчи – это семейство корневых деревьев, для которого выполняются следующие свойства (инварианты): Инвариант 1. Каждая
- 45. DecreaseKey (уменьшение ключа) -1 3 5 2 9 7 8 1 7 8 2 5 6
- 46. 3 5 2 9 7 8 1 7 8 2 9 9 cut(7) cut'(2) cut'(1) Восстановление
- 47. Предположим, что мы выполнили некоторое число исходных операций cut, а они привели к выполнению серии порождённых
- 48. Усреднённая оценка трудоемкости операции добавления нового элемента: Усреднённая оценка трудоемкости операции уменьшения ключа (задана ссылка на
- 49. Применение на практике
- 50. ExtractMin() — удаление минимального ключа; Heapify — строим бинарную кучу для последовательности из n ключей. 2.
- 51. C++ std::sort() Основой служит алгоритм быстрой сортировки – модифицированный QuickSort, он же IntroSort, разработанный специально для
- 52. Сжатие информации. Алгоритм префиксного кодирования Хаффмана
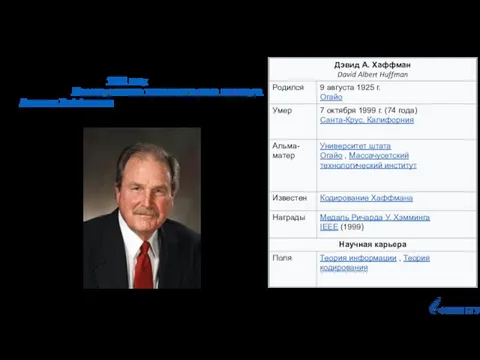
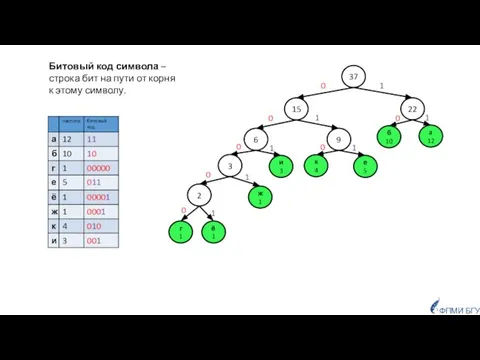
- 53. Метод разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы
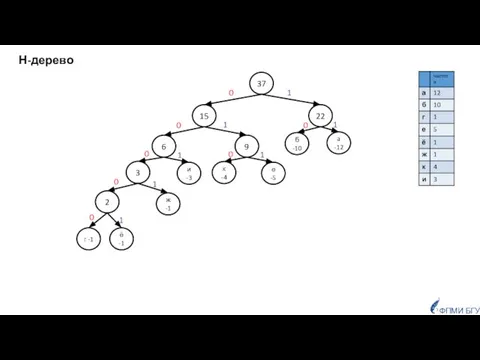
- 54. На вход поступает текст. По тексту строится таблица частот встречаемости символов. Строится дерево кодирования Хаффмана (Н-дерево).
- 55. Каждому символу ставим в соответствие узел дерева, вес узла – частота встречаемости символа в тексте. Полагаем
- 56. 2 ё -1 г -1 и -3 6 к -4 3 ж -1 б -10 15
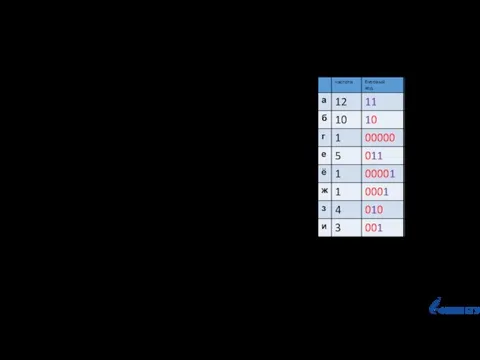
- 57. 2 ё 1 г 1 и 3 6 к 4 3 ж 1 б 10 15
- 58. Текст : кажжекaa … Закодированный текст: Кодирование: (010)(11 )( 0001)(0001)(011)(010)(11)(11) к а ж ж е к
- 59. 2 ё -1 г -1 и -3 6 к -4 3 ж -1 б -10 15
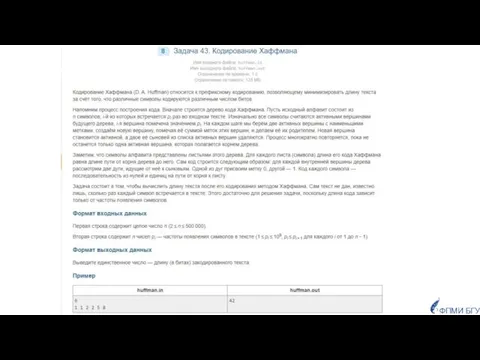
- 60. ЗАДАЧА На вход поступает таблица частот встречаемости символов текста, который будет закодирован классическим алгоритмом Хаффмана. Вам
- 61. 2 ё -1 г -1 и -3 6 к -4 3 ж -1 б -10 15
- 62. Какое время работы у Вашего «наивного алгоритма»? Разработайте более эффективный алгоритм и проверьте себя, решив эту
- 64. ??? ЗАДАНИЕ Выполнить общие задачи в iRunner Тема 3. Структуры данных 0.3. Бинарная куча (проверка на
- 66. Скачать презентацию







![def ExtractMin(a): a[0] = a[len(a) - 1] a.pop() i = 0 while](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/856419/slide-15.jpg)
































 Списки. Ссылки. Редактирование текста
Списки. Ссылки. Редактирование текста Понятие и классификация компьютерных сетей. Топология связей в компьютерных сетях
Понятие и классификация компьютерных сетей. Топология связей в компьютерных сетях Аспектно-ориентированный подход к архитектурно-независимому программированию вычислительных систем - язык [email protected]
Аспектно-ориентированный подход к архитектурно-независимому программированию вычислительных систем - язык [email protected] Компьютерный класс будущего
Компьютерный класс будущего Приключенческая сага
Приключенческая сага Использование компьютера на уроках технологии
Использование компьютера на уроках технологии Трофимооовв
Трофимооовв Классификация и разновидности объектов
Классификация и разновидности объектов Full-Stack Web Development with React (Онлайн, Coursera, ENG, ОК)
Full-Stack Web Development with React (Онлайн, Coursera, ENG, ОК) Современные интернет-коммуникации - соцсети
Современные интернет-коммуникации - соцсети Основы программирования C++
Основы программирования C++ Массивы и их сортировка
Массивы и их сортировка Биоинформатическая обработка NGS-данных
Биоинформатическая обработка NGS-данных Библиографическое описание документа
Библиографическое описание документа Создание графических изображений
Создание графических изображений Создание авторской настольной игры
Создание авторской настольной игры Инфорка
Инфорка Структуры данных и алгоритмы. Дружественные классы и функции
Структуры данных и алгоритмы. Дружественные классы и функции Исследовательская деятельность как интеграция физики и информатики
Исследовательская деятельность как интеграция физики и информатики Software Testing 2/10 WELCOME
Software Testing 2/10 WELCOME Развитие мотивационного компонента творческого потенциала обучающихся на уроках информатики
Развитие мотивационного компонента творческого потенциала обучающихся на уроках информатики Базы данных. Что это?
Базы данных. Что это? Как прикрепить задание в системе Сетевой город. Образование
Как прикрепить задание в системе Сетевой город. Образование Компьютерные программы
Компьютерные программы Презентация на тему Исследование биологической модели
Презентация на тему Исследование биологической модели  Клуб Roy. Сервис совместного парамайнинга криптовалюты Prizm
Клуб Roy. Сервис совместного парамайнинга криптовалюты Prizm Введение в объектноориентированное программирование. Параметризованные типы
Введение в объектноориентированное программирование. Параметризованные типы BMWSTART (1)
BMWSTART (1)