Содержание
- 2. Степени числа 2 1.Степени 2. Ответы: 23 24 25 26 27 28 21 22 20 8
- 3. Проверяем 1. Степени числа 2 23 = 2*2*2=8 24 = 2*2*2*2=16 25 = 32 26 =64
- 4. Как измерить информацию? Ответ на него зависит от того, что понимать под информацией. Но поскольку определять
- 6. Алфавитный подход - это способ измерения информационного объема текста, не связанного с его содержанием. Рассмотрим один
- 7. Основоположником этого подхода является Андрей Николаевич Колмогоров, (1903-1987), великий российский ученый-математик.
- 8. Алфавитный подход каждый символ несёт одинаковое количество информации частота появления разных символов (и сочетаний символов) не
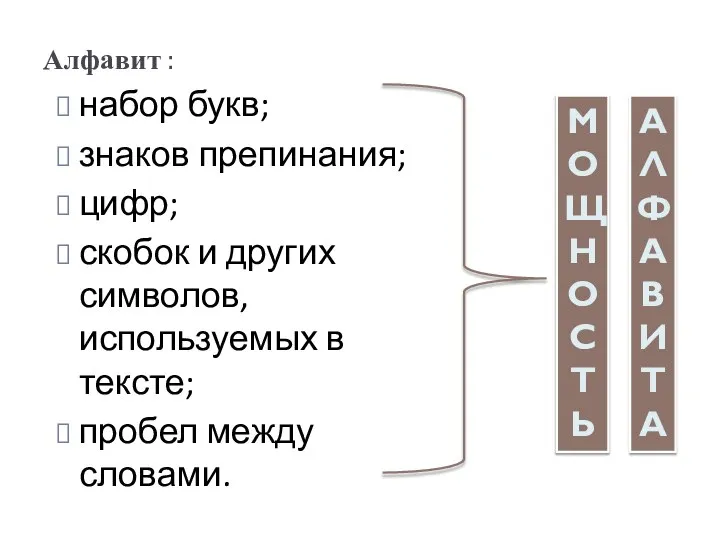
- 9. Алфавит : набор букв; знаков препинания; цифр; скобок и других символов, используемых в тексте; пробел между
- 10. МОЩНОСТЬ РУССКОГО АЛФАВИТА: 33 буквы 10 цифр 11 знаков препинания скобки пробел 54
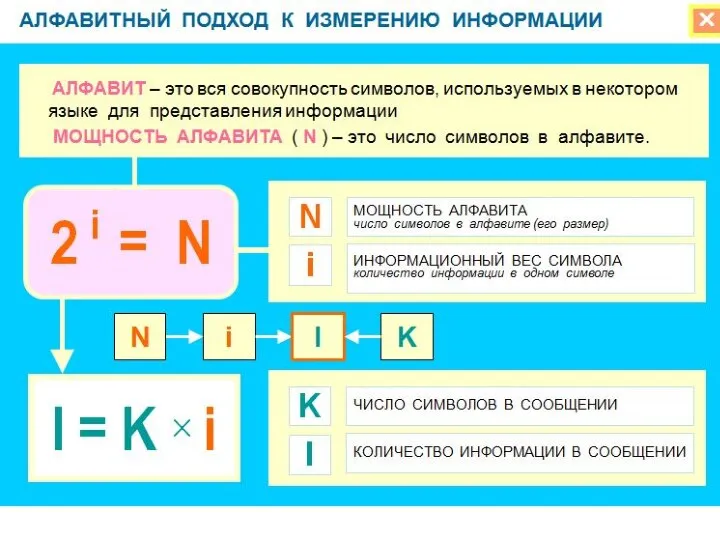
- 11. N = 2i, где i - информационный вес символа. N – мощность алфавита
- 12. I = K*i, где I – информационный объем текста. K - количество символов в тексте. i
- 14. Примеры алфавитов Самое наименьшее число символов в алфавите: 2 (0 и 1) - двоичный алфавит. Информационный
- 15. Алфавит, из которого составляется «компьютерный текст», содержит 256 символов. N = 2i 256 = 28 следовательно,
- 16. Единицы измерения информации: 1 байт = 8 битам 1 Килобайт = 1Кб=210 байт =1024 байта; 1
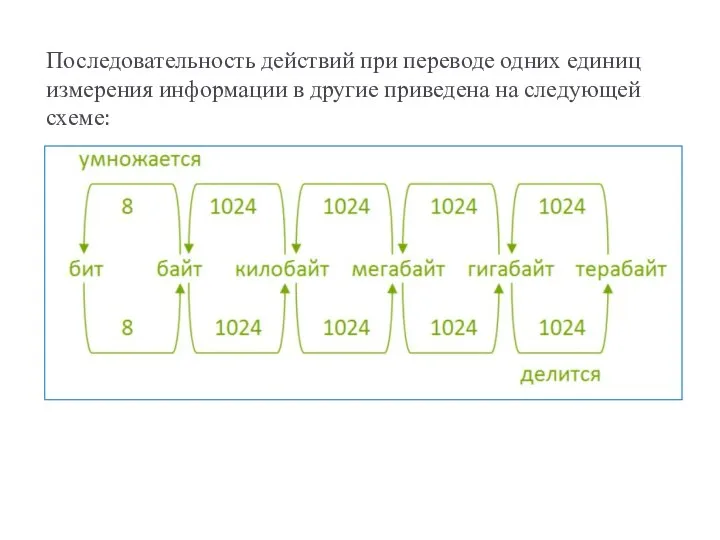
- 17. Последовательность действий при переводе одних единиц измерения информации в другие приведена на следующей схеме:
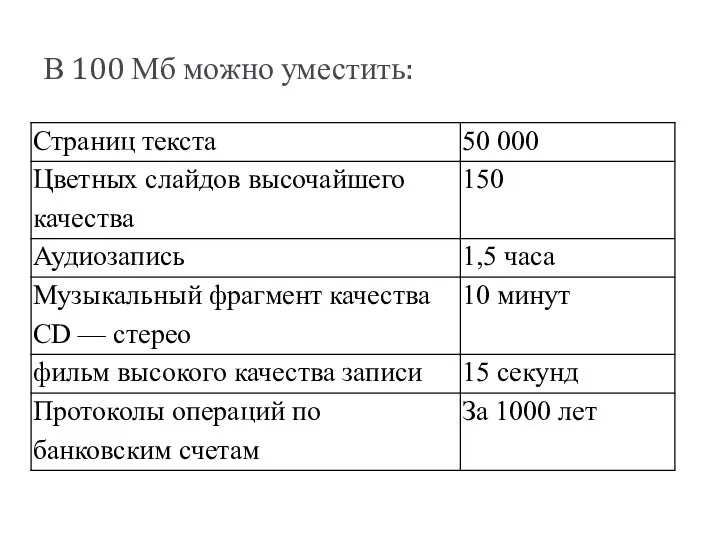
- 18. В 100 Мб можно уместить:
- 19. Задача Посчитать количество информации в следующем двоичном тексте 110011111100101000101011. Нужно пересчитать все 0 и 1. Всего
- 20. Задача Определить количество информации в 10 страницах текста (на каждой странице 32 строки по 64 символа)
- 21. Вариант 1 (Уровень А). Алфавит племени содержит всего 8 букв. Какое количество информации несет одна буква
- 22. Заполните пропуски
- 23. Проверяем Вариант 2 Дано: N=64, К=20 Найти: I Решение: N = 2i 64= 26 Это значит,
- 24. Проверяем
- 25. Задачи: текст (дополнительно) Сколько места в памяти надо выделить для хранение предложения Привет, Вася! считаем все
- 26. Задача: Сколько места надо выделить для хранения 10 страниц книги, если на каждой странице помещаются 32
- 27. Скорость передачи информации Прием-передача информации могут происходить с разной скоростью. Количество информации, передаваемое за единицу времени,
- 28. Домашнее задание
- 30. Скачать презентацию






















 Проблемы надёжности и безопасности хранения и передачи информации
Проблемы надёжности и безопасности хранения и передачи информации Вычисление площади поверхности конуса в табличном процессоре MS Excel
Вычисление площади поверхности конуса в табличном процессоре MS Excel Методы и средства обеспечения безопасности. Критерии оценки безопасности информационных технологий
Методы и средства обеспечения безопасности. Критерии оценки безопасности информационных технологий Электронные таблицы
Электронные таблицы Система управления базами данных
Система управления базами данных Базы данных - 5
Базы данных - 5 Стандарт шифрования данных DES (Data Encryption Standard)
Стандарт шифрования данных DES (Data Encryption Standard) Человек и информация. 5 класс
Человек и информация. 5 класс Терминологический глоссарий для начинающих программистов
Терминологический глоссарий для начинающих программистов Федеральный реестр сведений о документах об образовании и о квалификации, документах об обучении
Федеральный реестр сведений о документах об образовании и о квалификации, документах об обучении Винни-Пух и пчелы
Винни-Пух и пчелы Анимации
Анимации Стайный алгоритм
Стайный алгоритм Алгоритмизация и программирование. Обзор языка программирования С#. (Лекция 2)
Алгоритмизация и программирование. Обзор языка программирования С#. (Лекция 2) Сетевые информационные технологии
Сетевые информационные технологии Как компьютерный вирус проникает в компьютер?
Как компьютерный вирус проникает в компьютер? Дизайн. Творческий мир социальных сетей. Создание артов
Дизайн. Творческий мир социальных сетей. Создание артов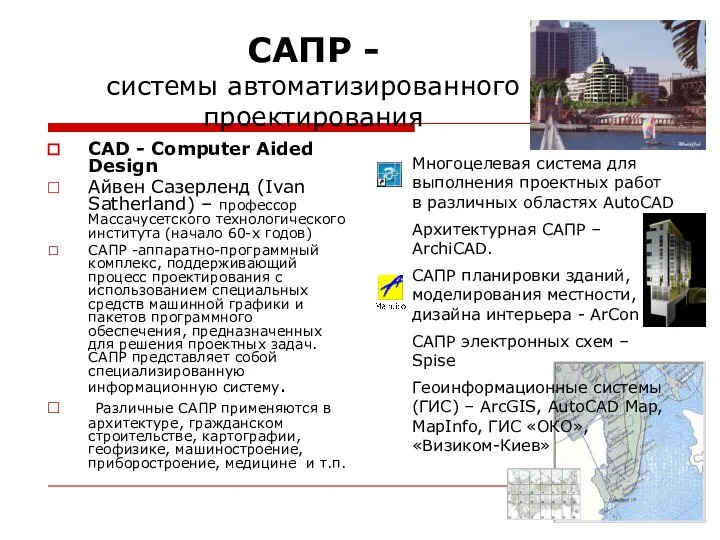 САПР - системы автоматизированного проектирования
САПР - системы автоматизированного проектирования Интеллектуальная информационная система сортировки томатов
Интеллектуальная информационная система сортировки томатов Компьютер и его ПО. Глава 2
Компьютер и его ПО. Глава 2 Social media and pandemic
Social media and pandemic Информационный запас слова и его измерение
Информационный запас слова и его измерение Пакеты прикладных программ. Модуль 1
Пакеты прикладных программ. Модуль 1 Разработка алгоритмов управления и протокола общения систем различных автономных объектов роботизированного полигона города
Разработка алгоритмов управления и протокола общения систем различных автономных объектов роботизированного полигона города Доклад Вставка изображений. 4 класс
Доклад Вставка изображений. 4 класс Расширения алгоритмов LLE, Isomap, MDS, Eigenmaps, и Spectral Clustering для точек вне обучающей выборки
Расширения алгоритмов LLE, Isomap, MDS, Eigenmaps, и Spectral Clustering для точек вне обучающей выборки Социальные сети
Социальные сети Использование графического браузера
Использование графического браузера