Системы массового обслуживания (продолжение 1)

2
Одноканальная система М / М / 1 с ожиданием
В предыдущих пунктах мы рассматривали простейшие системы массового обслуживания, в которых не было очереди, соответственно, ожидания обслуживания. Но большинство реальных систем имеют блок ожидания. В данной модели имеется единственный узел обслуживания, а на вместимость блока ожидания и емкость источника требований никаких ограничений не накладывается (рис. 7).
Рис. 7. Одноканальная система массового обслуживания с ожиданием
Входной и выходной потоки являются пуассоновскими с параметрами λ и μ соответственно (рис. 8).

3
Рис. 8. Входной и выходной потоки одноканальной системы
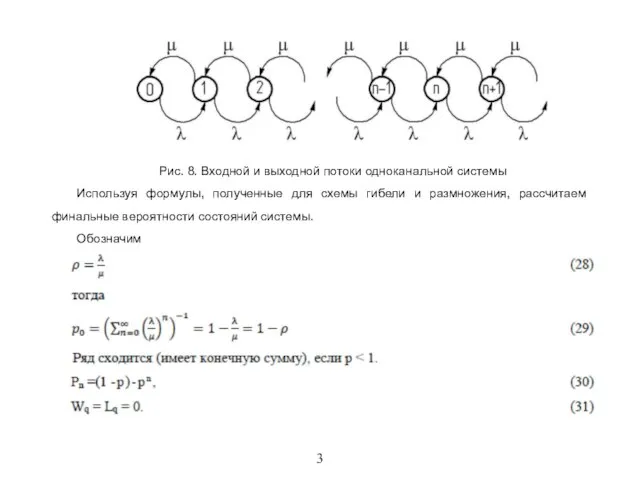
Используя формулы, полученные для схемы гибели и размножения, рассчитаем финальные вероятности состояний системы.
Обозначим

4
Пример 4. Собранные сведения о работе моечной станции показывают, что автомобили поступают на эту станцию в соответствии с пуассоновским распределением со средним 5 автомобилей в час. Каждый клиент требует своего набора услуг, поэтому продолжительность выполнения работ для каждого автомобиля также случайная величина,

5
Станция одновременно может обслуживать только один автомобиль. Определить основные характеристики системы: средняя длина очереди, среднее время пребывания автомобиля на станции, среднее время простоя станции.
Решение: Сначала получим интенсивность потока транспорта и интенсивность обслуживания в час:
λ = 5, ? = 60 / 10 =6
Тогда средняя длина очереди
Среднее время пребывания автомобилей на моечной станции в ожидании обслуживания и на обслуживании
?? =1 / (?−λ) = 1
то есть обслуживание в среднем займет один час, при этом моечная станция будет простаивать тогда, когда на ней не будет автомобилей
?0 = 1−? =1 / 6 ≈ 0,17
поэтому 17% времени моечная станция будет простаивать.

6
Система с конечной очередью М / М / 1 / N
Разница между этой моделью и рассмотренной выше заключается только в том, что максимальное число требований, допускаемых в систему, ограничено N (то есть максимальное число требований в очереди N-1 и одно требование на обслуживании). Это означает, что при наличии в системе N требований ни одна из дополнительных заявок на обслуживание не может присоединиться к очереди в блоке ожидания. В результате эффективная частота поступлений требований (требований, которые будут обслужены) для указанной системы становится меньше общего потока требований (рис. 9).
Рис. 9 - Одноканальная система массового обслуживания с ожиданием и ограничением очереди

7
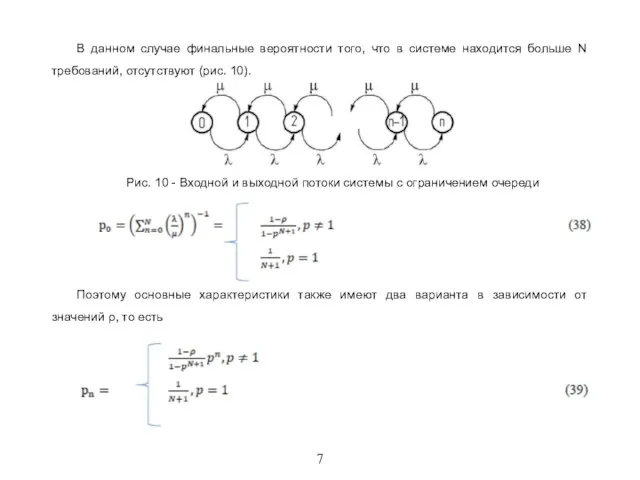
В данном случае финальные вероятности того, что в системе находится больше N требований, отсутствуют (рис. 10).
Рис. 10 - Входной и выходной потоки системы с ограничением очереди
Поэтому основные характеристики также имеют два варианта в зависимости от значений ρ, то есть

8
В данном случае финальные вероятности того, что в системе находится больше N требований, отсутствуют (рис. 10).

9
Пример 5. Вспомним пример для предыдущей модели (пример 4). На этот раз у моечной станции оборудовано 5 стоянок для размещения автомобилей, ожидающих обслуживания. Если все площадки заняты, то дополнительно пребывающие автомобили вынуждены искать другую станцию.
Для моечной станции интересно оценить, сколько клиентов она теряет из-за ограниченности мест стоянки, а также оценить среднее количество мест стоянки, которые будут заняты, и среднее время обслуживания автомобиля.
Решение: В рассматриваемом примере число мест в системе
N = 5 +1 = 6,
а отношение интенсивности поступления требований и интенсивности их обслуживания
? = λ / ? = 56
Тогда вероятность того, что все места в системе заняты
Отсюда следует, что в среднем в час будет отказано следующему числу клиентов
λотк = λ • PN = 5 • 0,0774 = 0,387

10
Средняя очередь или количество автомобилей на стоянке
Время обслуживания в такой системе составляет примерно полчаса, что значительно меньше, чем при неограниченном количестве мест на стоянке (1 ч.).
Многоканальная система с ожиданием М / М / с
Система массового обслуживания, описываемая данной моделью, функционирует так, что при входном потоке λ требования параллельно могут обслуживаться на с приборах, каждый из которых имеет интенсивность обслуживания μ (рис. 11).
Рис. 11. Многоканальная система М / М / с

11
Входной и выходной потоки являются пуассоновскими. Цель использования нескольких приборов в повышении скорости обслуживания клиентов (по сравнению с одноканальной системой).
В данной модели интенсивность обслуживания зависит от количества требований в системе. При количестве требований n > с интенсивность обслуживания cμ. При количестве требований n < с интенсивность обслуживания nμ. (рис 12).
Рис. 5.12. Схема функционирования многоканальной системы
В данном случае формулы процесса гибели и размножения дадут следующий результат:

12

13
Пример 6. В небольшом городе функционируют две службы такси, принадлежащие разным фирмам. Каждая из служб располагает двумя автомобилями. При этом заказы на обслуживание, согласно имеющимся сведениям, распределяются между службами поровну. В диспетчерские службы обеих фирм поступает в среднем 10 вызовов в час. Среднее время обслуживания одного клиента 11,5 минут. Вызовы такси распределены по пуассоновскому закону, а время обслуживания распределено экспоненциально.
Эти две фирмы покупает третья сторона - фирма «Стрела». Необходимо рассчитать, как изменятся основные характеристики функционирования такси при объединении диспетчерских служб.
Решение: До объединения каждая фирма работала как система М / М / 2 с потоком заказов λ = 10, а после объединения - как система М / М / 4 с потоком заказов λ = 10 + 10 = 20 (до объединения в каждой фирме было по два автомобиля, а в фирме «Стрела» их четыре).
В каждой из этих служб коэффициент загруженности высок
то есть составляет 95,8%. Но в фирме «Стрела» такая нагрузка сохраняется

14
Но эффект в объединении диспетчерских служб отражается в других характеристиках. Рассчитаем среднее время ожидания клиентом такси. При с = 2 отношение равно