Содержание
- 2. Логические выражения представляет собой Высказывания являющиеся повествовательным предложением которые содержат утверждение в отношении которого можно однозначно
- 3. Высказывания бывают общими, частными или единичными. Общее высказывание начинается (или можно начать) со слов: все, всякий,
- 4. Пример Определить тип высказывания (общее, частное, единичное) «Все рыбы умеют плавать» «Некоторые медведи-бурые» «Буква А-гласная»
- 5. В логических выражениях высказывания как правило обозначается заглавными латинскими буквами Высказывания образованные из других высказываний с
- 6. Логические связки рассматривают как операции над высказываниями, при этом если известно значение исходных высказываний, значение составного
- 7. и задается следующей таблицей истинности
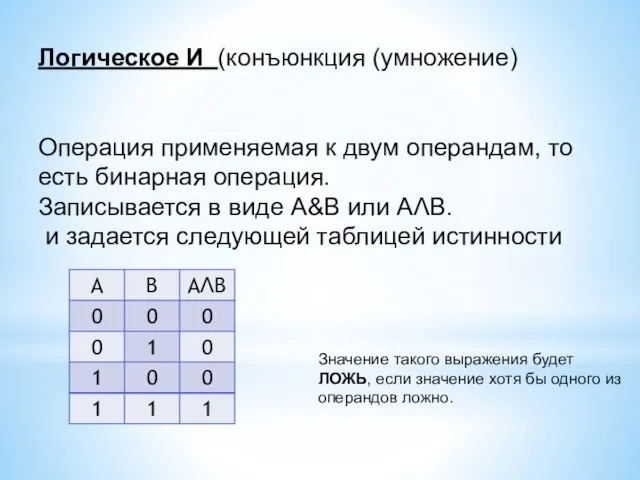
- 8. Логическое И (конъюнкция (умножение) Операция применяемая к двум операндам, то есть бинарная операция. Записывается в виде
- 9. Логическое ИЛИ (дизъюнкция (сложение) Еще одна бинарная операция. В математической логике используется знак V и записывается
- 10. Существует также производные логические операции которые применяются при составлении выражений, но при дальнейшем анализе могут быть
- 11. Импликация (если, то) Записывается в виде А →В, А ⇒В или ⊃. и задается следующей таблицей
- 12. Эквиваленция (тогда и только тогда) Записывается в виде А ≡ В, А ↔ В. и задается
- 14. Скачать презентацию










 Устройства компьютера
Устройства компьютера Услуги компьютерных сетей. Удаленная база данных
Услуги компьютерных сетей. Удаленная база данных 3D панорама
3D панорама Критерии приемки и определение выполненного
Критерии приемки и определение выполненного Операционные системы
Операционные системы INEX. Главное меню
INEX. Главное меню Технологии передачи информации
Технологии передачи информации Представление целых и вещественных чисел в памяти ПК
Представление целых и вещественных чисел в памяти ПК Read and translate the poster
Read and translate the poster Какво представлява WebAssembly
Какво представлява WebAssembly Обработка информации. Практическая работа
Обработка информации. Практическая работа ОТНОШЕНИЯ между ПОНЯТИЯМИ
ОТНОШЕНИЯ между ПОНЯТИЯМИ Презентация на тему Информация и информационные процессы
Презентация на тему Информация и информационные процессы  Почта и журналистика
Почта и журналистика Изучение системы технических средств защиты информации
Изучение системы технических средств защиты информации Основы программирования на языке Python
Основы программирования на языке Python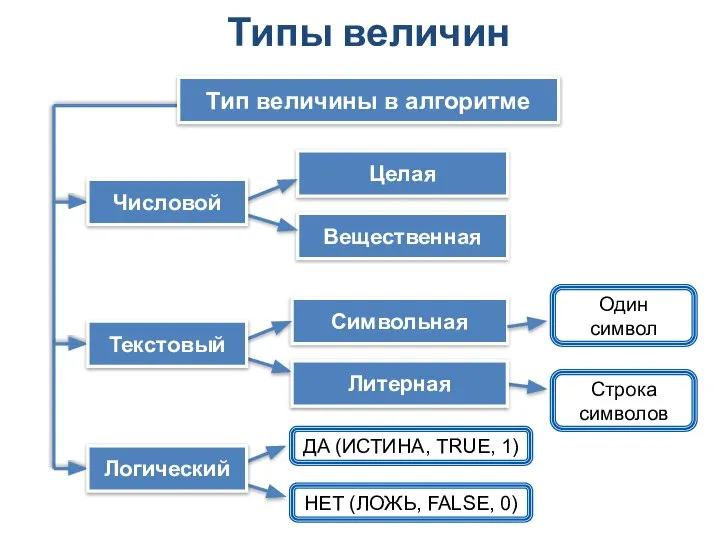 Типы величин. Тип величины в алгоритме
Типы величин. Тип величины в алгоритме Презентация на тему Действия с информацией
Презентация на тему Действия с информацией 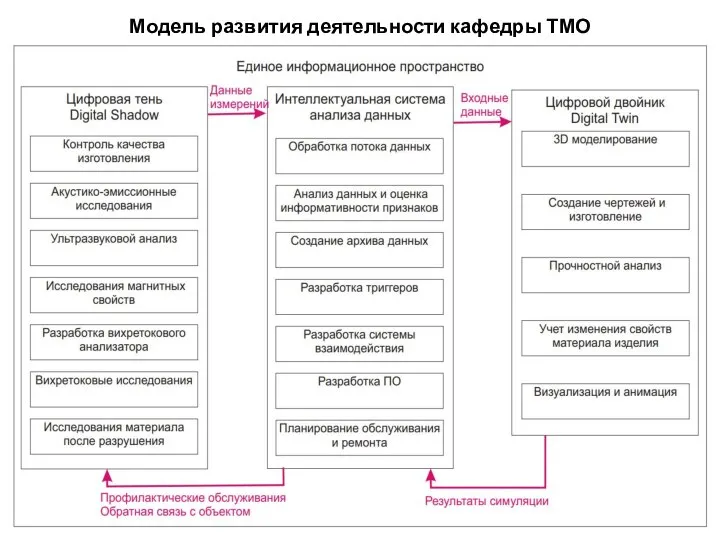 Модель развития деятельности кафедры ТМО
Модель развития деятельности кафедры ТМО Информационные технологии
Информационные технологии Текстовый редактор
Текстовый редактор Настройка подключения к Веб ГИС
Настройка подключения к Веб ГИС Динамическое распределение памяти
Динамическое распределение памяти Електронна оплата за транспортні послуги у громадському транспорті
Електронна оплата за транспортні послуги у громадському транспорті Лекция 1
Лекция 1 Персональный компьютер
Персональный компьютер Организация конкурсного движения в социальных сетях как форма цифрового взаимодействия с семьями воспитанников ДОУ
Организация конкурсного движения в социальных сетях как форма цифрового взаимодействия с семьями воспитанников ДОУ Использование Linux при программировании 1
Использование Linux при программировании 1