Слайд 2Задан взвешенный граф с N вершинами и M рёбрами. Для каждого ребра

задано его расстояние – неотрицательная величина. Требуется найти минимальное расстояние от вершины 1 до всех остальных вершин (вариант – минимальное расстояние между заданной парой вершин).
Слайд 3Типы пометок вершин
отсутствует – не найдено ни одного пути до этой вершины;
временная

– путь найден, но он, возможно, не минимален;
постоянная – найден минимальный путь
Слайд 41
6
7
8
9
10
5
4
3
2
5
2
11
3
17
3
24
25
2
4
21
9
7
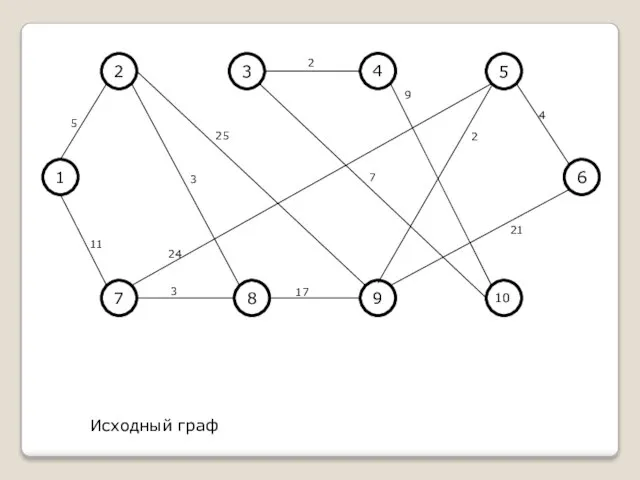
Исходный граф
Слайд 51
6
7
8
9
10
5
4
3
2
5
2
12
3
17
3
24
25
2
4
21
9
7
Заносим в кучу информацию о начальной вершине 1.
Длина пути до неё
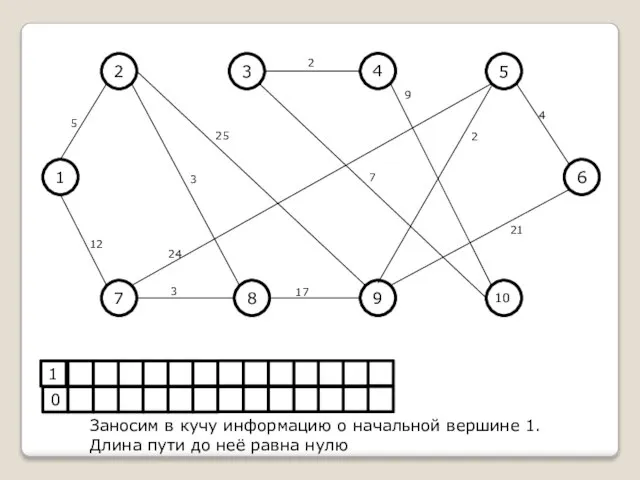
равна нулю
Слайд 61
6
7
8
9
10
5
4
3
2
5
2
12
3
17
3
24
25
2
4
21
9
7
0
12
5
Извлекаем вершину 1, делаем её пометку постоянной.
Пересчитываем длину пути до вершин 2
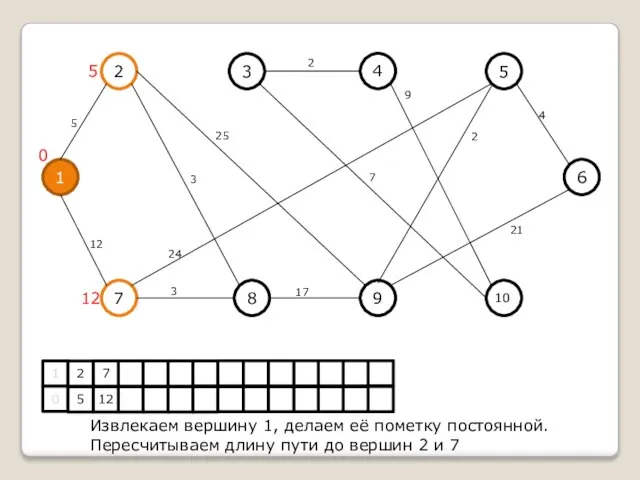
и 7
Слайд 71
6
7
8
9
10
5
4
3
2
5
2
12
3
17
3
24
25
2
4
21
9
7
0
12
5
30
8
Извлекаем вершину 2, делаем её пометку постоянной.
Пересчитываем длину пути до вершин 8
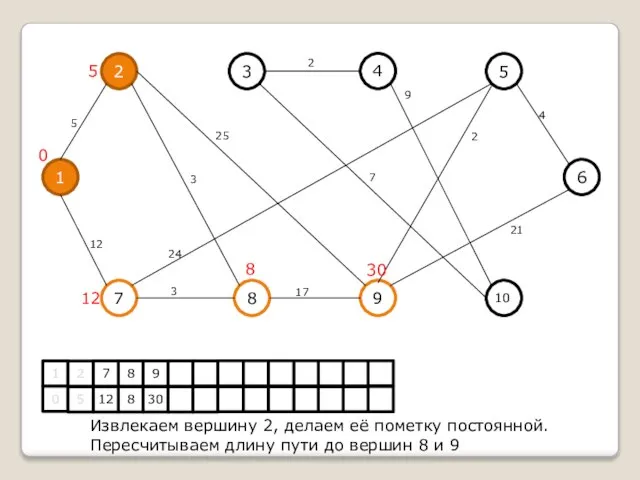
и 9
Слайд 81
6
7
8
9
10
5
4
3
2
5
2
12
3
17
3
24
25
2
4
21
9
7
0
11
5
25
8
Извлекаем вершину 8, делаем её пометку постоянной.
Пересчитываем длину пути до вершин 7
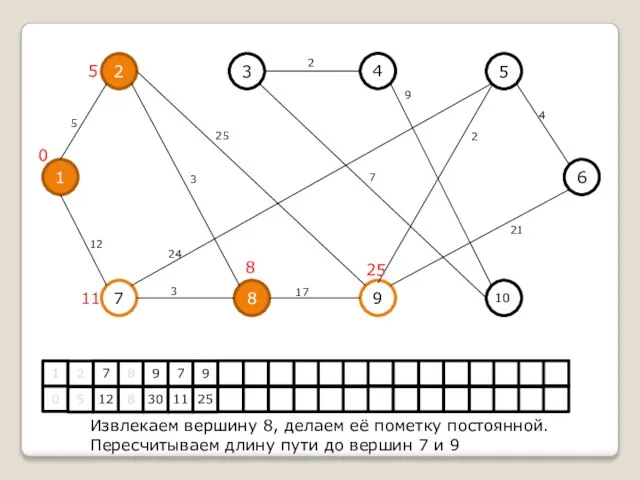
и 9
Слайд 91
6
7
8
9
10
5
4
3
2
5
2
12
3
17
3
24
25
2
4
21
9
7
0
11
5
25
8
35
Извлекаем вершину 7, делаем её пометку постоянной.
Пересчитываем длину пути до вершины 5
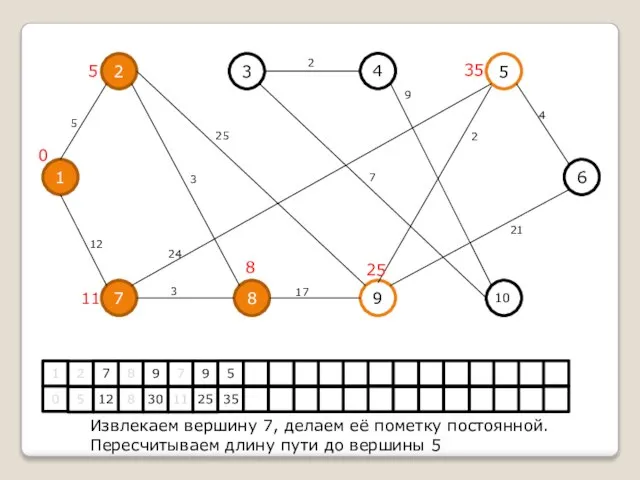
Слайд 101
6
7
8
9
10
5
4
3
2
5
2
12
3
17
3
24
25
2
4
21
9
7
0
11
5
25
8
35
Извлечённая вершина 7 имеет постоянную пометку
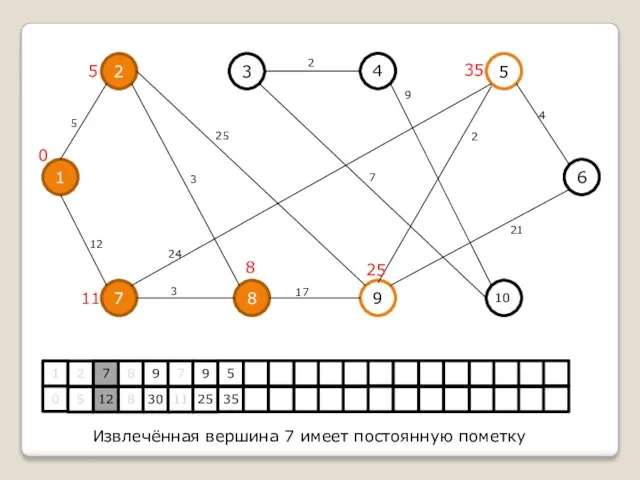
Слайд 111
6
7
8
9
10
5
4
3
2
5
2
12
3
17
3
24
25
2
4
21
9
7
0
11
5
25
8
27
46
Извлекаем вершину 9, делаем её пометку постоянной.
Пересчитываем длину пути до вершин 5
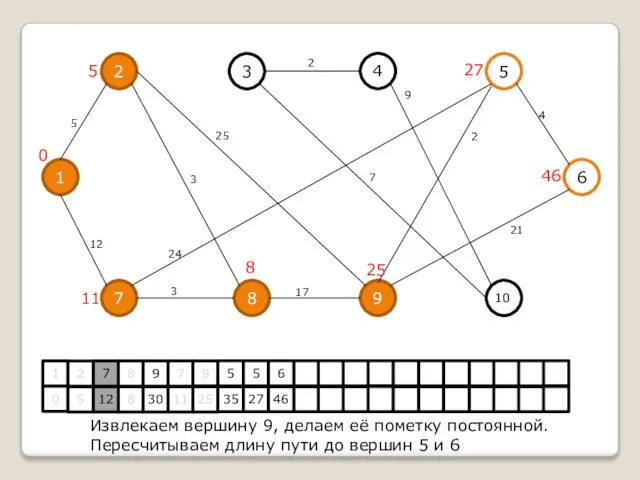
и 6
Слайд 121
6
7
8
9
10
5
4
3
2
5
2
12
3
17
3
24
25
2
4
21
9
7
0
11
5
25
8
27
31
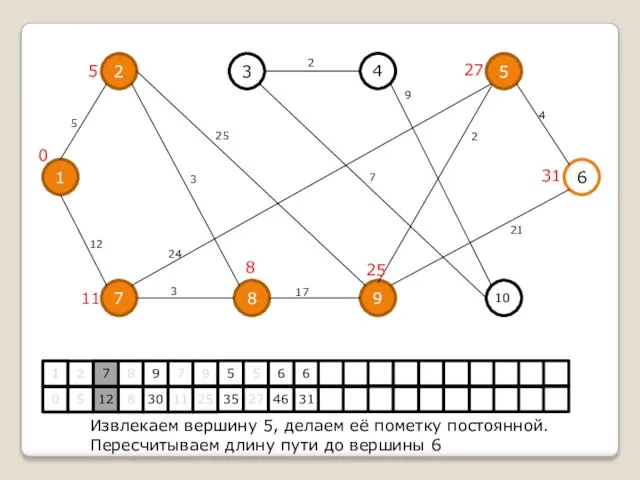
Извлекаем вершину 5, делаем её пометку постоянной.
Пересчитываем длину пути до вершины 6
Слайд 131
6
7
8
9
10
5
4
3
2
5
2
12
3
17
3
24
25
2
4
21
9
7
0
11
5
25
8
27
31
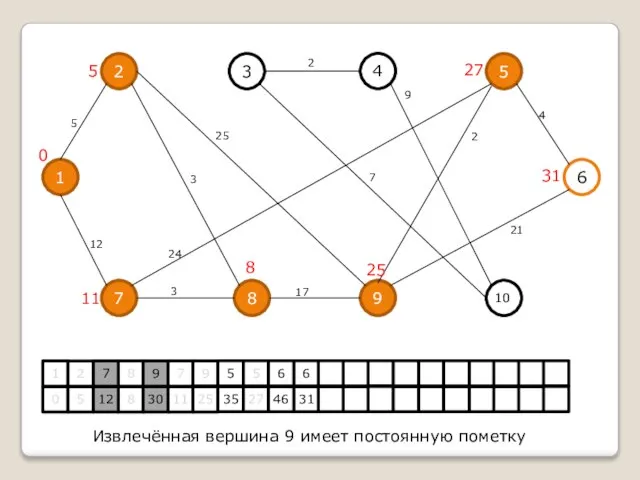
Извлечённая вершина 9 имеет постоянную пометку
Слайд 141
6
7
8
9
10
5
4
3
2
5
2
12
3
17
3
24
25
2
4
21
9
7
0
11
5
25
8
27
31
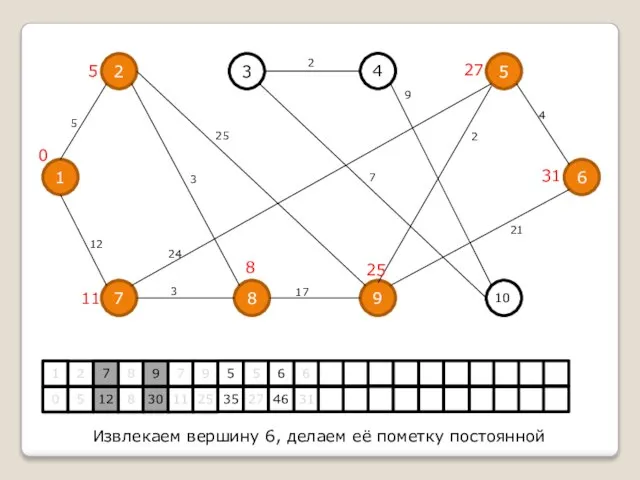
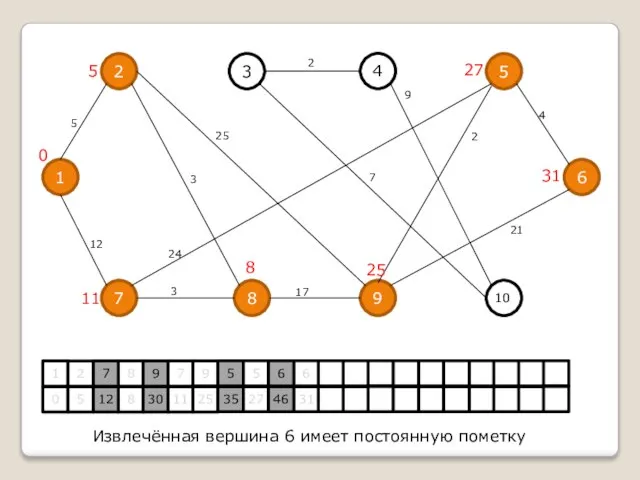
Извлекаем вершину 6, делаем её пометку постоянной
Слайд 151
6
7
8
9
10
5
4
3
2
5
2
12
3
17
3
24
25
2
4
21
9
7
0
11
5
25
8
27
31
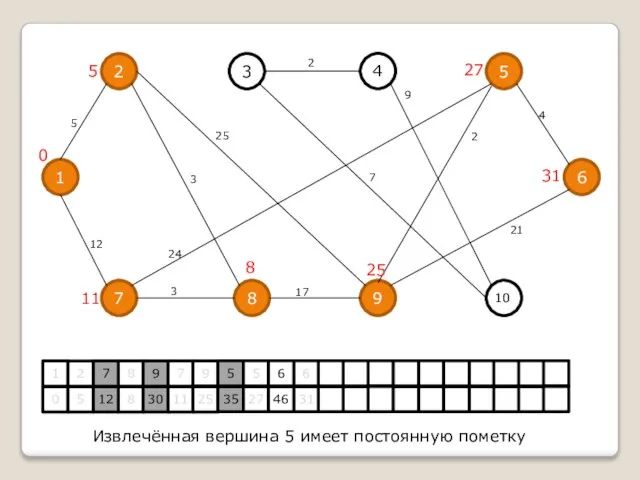
Извлечённая вершина 5 имеет постоянную пометку
Слайд 161
6
7
8
9
10
5
4
3
2
5
2
12
3
17
3
24
25
2
4
21
9
7
0
11
5
25
8
27
31
Извлечённая вершина 6 имеет постоянную пометку















 Особенности компьютерно-опосредованной коммуникации
Особенности компьютерно-опосредованной коммуникации Эргономика рабочего места пользователя ПК
Эргономика рабочего места пользователя ПК Обучающее приложение для детей
Обучающее приложение для детей 10-04-Процедуры ввода-вывода
10-04-Процедуры ввода-вывода Просвещенный абсолютизм
Просвещенный абсолютизм Ответ на тест
Ответ на тест Форматирование текста на Web-странице
Форматирование текста на Web-странице Конкурентный анализ
Конкурентный анализ Visa application
Visa application Практическая работа. Excel
Практическая работа. Excel 8-3-1
8-3-1 Урок 5. Типы контента в социальных сетях. Принципы копирайтинга
Урок 5. Типы контента в социальных сетях. Принципы копирайтинга Работа с записями базы данных
Работа с записями базы данных Время думать. Информатика
Время думать. Информатика Программирование в среде Robot C. Арифметические действия
Программирование в среде Robot C. Арифметические действия Операторы языка C#. (Лекция 3)
Операторы языка C#. (Лекция 3) Компьютерные сети
Компьютерные сети Современные компьютерные технологии в деятельности государственных служащих
Современные компьютерные технологии в деятельности государственных служащих Лето в Кванториуме
Лето в Кванториуме ОС для мобильных устройств. Windows Mobile
ОС для мобильных устройств. Windows Mobile Двоичное кодирование
Двоичное кодирование Информационно-коммуникационные технологии в связи
Информационно-коммуникационные технологии в связи Программный комплекс ИС БТИ
Программный комплекс ИС БТИ Работа с текстом
Работа с текстом Створення текстових документів
Створення текстових документів Презентация на тему Работа в сети Интернет. Электронная почта
Презентация на тему Работа в сети Интернет. Электронная почта  Электронный ЮУрГУ. Видеоконференция. Таджикский язык
Электронный ЮУрГУ. Видеоконференция. Таджикский язык Отправить сообщения на электронный адрес на темы Электронная почта
Отправить сообщения на электронный адрес на темы Электронная почта