Содержание
- 2. Цель урока: 1) Повторение и закрепление материала по темам: алгоритм, свойства алгоритма, представление алгоритмов, виды и
- 3. Под алгоритмом понимается понятное и точное предписание исполнителю совершить последовательность действий, направленных на достижение поставленной цели
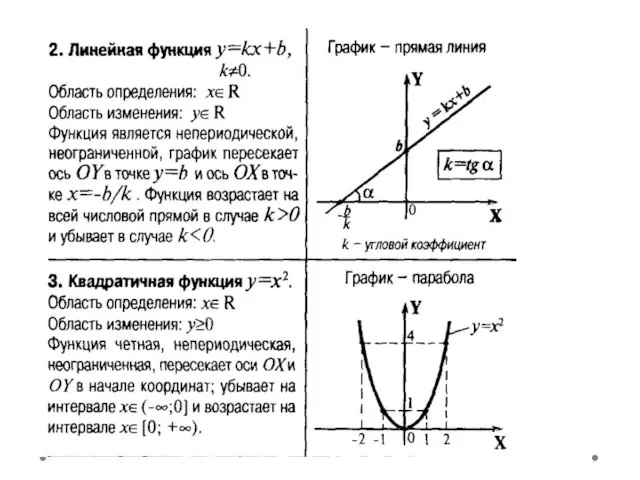
- 4. Виды графиков. Преобразование графиков.
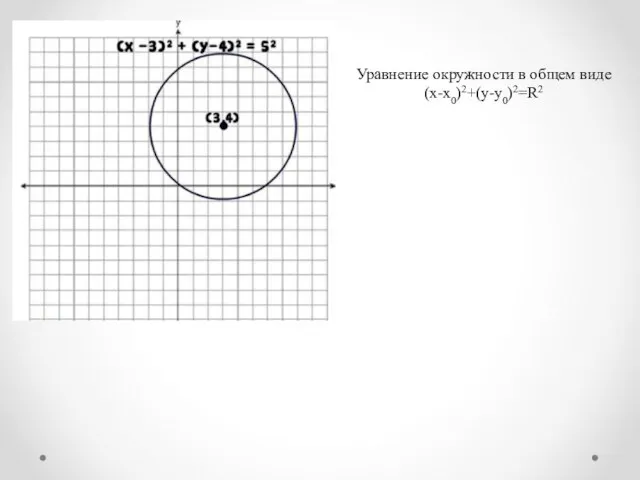
- 6. Уравнение окружности в общем виде (x-x0)2+(y-y0)2=R2
- 7. Преобразования относительно оси OY. Параллельный перенос. Сдвиг графика относительно оси OY , осуществляется, если необходимо построить
- 8. Преобразования относительно оси OX. Параллельный перенос. Параллельный перенос (сдвиг) графика относительно оси OX выполняют для построения
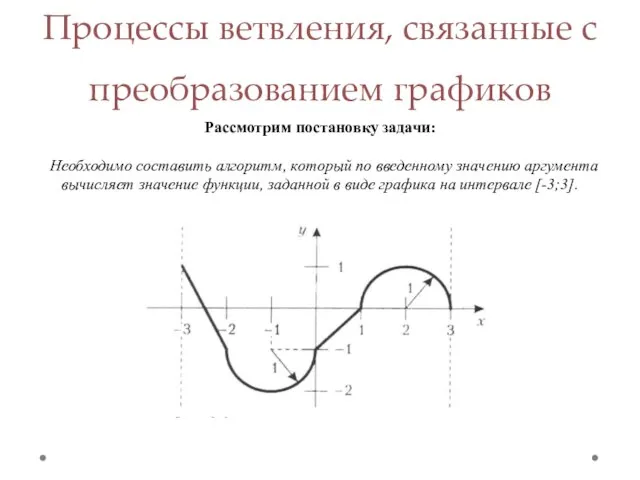
- 9. Процессы ветвления, связанные с преобразованием графиков Рассмотрим постановку задачи: Необходимо составить алгоритм, который по введенному значению
- 10. На промежутке [-3; -2) мы видим прямую, которая проходит через точки с координатами (-3; 1) и
- 11. Если аргумент x принадлежит интервалу [-2; 0), то это полуокружность радиусом 1, смещённая от начала координат
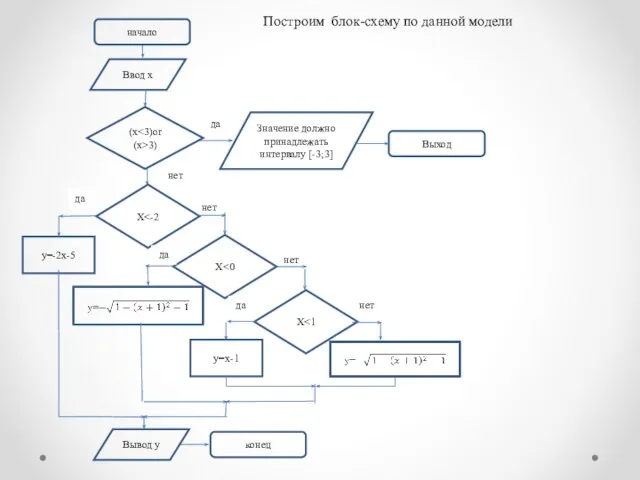
- 12. Построим блок-схему по данной модели
- 13. Фронтальная работа Необходимо составить алгоритм, который по введенному значению аргумента вычисляет значение функции. На каком интервале
- 15. Скачать презентацию








 МИФы нашей школы
МИФы нашей школы Презентация на тему Технологии обработки числовых данных
Презентация на тему Технологии обработки числовых данных  Интернет-маркетинговое агентство Smartnet 24. Внедрение Битрикс24.CRM
Интернет-маркетинговое агентство Smartnet 24. Внедрение Битрикс24.CRM L3_CSMA_CD
L3_CSMA_CD Разработка обучающего веб-сайта по корейскому языку
Разработка обучающего веб-сайта по корейскому языку Операционные системы
Операционные системы Проблематика отзывных площадок
Проблематика отзывных площадок Приём заявлений в 1 класс. Алгоритм подачи заявления в электронном виде
Приём заявлений в 1 класс. Алгоритм подачи заявления в электронном виде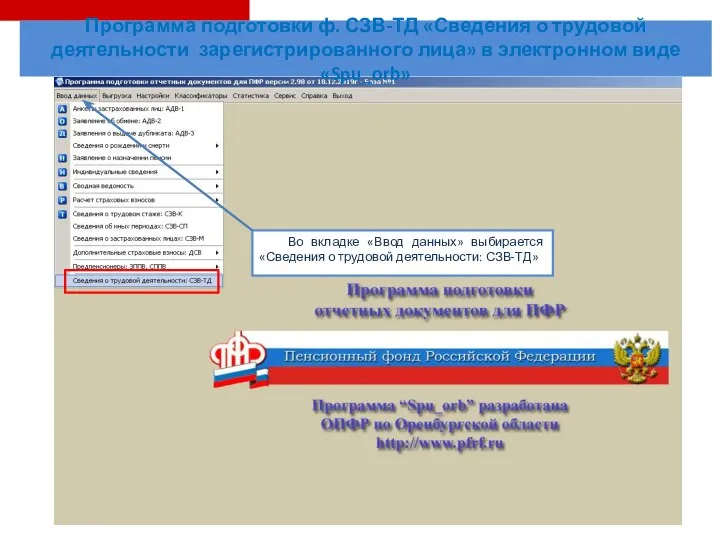 Программа подготовки СЗВ-ТД Сведения о трудовой деятельности зарегистрированного лица в электронном виде Spu_orb
Программа подготовки СЗВ-ТД Сведения о трудовой деятельности зарегистрированного лица в электронном виде Spu_orb SimbirSoft. Сквозной проект. Основы программирования
SimbirSoft. Сквозной проект. Основы программирования Проект Coursera
Проект Coursera СВАН-анализ
СВАН-анализ Файловые менеджеры
Файловые менеджеры Базы данных
Базы данных Создание электронных тестов
Создание электронных тестов Программное обеспечение компьютера
Программное обеспечение компьютера Искусственные и естественные источники информации
Искусственные и естественные источники информации Математическое программное обеспечение автоматизированных систем управления
Математическое программное обеспечение автоматизированных систем управления Моушен дизайн
Моушен дизайн Мессенджер Telegram: портрет пользователей
Мессенджер Telegram: портрет пользователей SQL. Structured Query Language. Структурированный язык запросов
SQL. Structured Query Language. Структурированный язык запросов Оптимизация Photoshop
Оптимизация Photoshop Презентация на тему Компьютеры и здоровье: анализ совместимости
Презентация на тему Компьютеры и здоровье: анализ совместимости  Средства автоматизации проектирования автоматизированных систем
Средства автоматизации проектирования автоматизированных систем Использование цифрового образовательного портала 5 , для реализации парциальной программы Предшкола нового поколения
Использование цифрового образовательного портала 5 , для реализации парциальной программы Предшкола нового поколения Чек-лист полезных ссылок для поиска работы
Чек-лист полезных ссылок для поиска работы Компьютерные сети, классификация
Компьютерные сети, классификация Способы поиска в интернете
Способы поиска в интернете