Алгоритмы работы с графами с использованием MapReduce

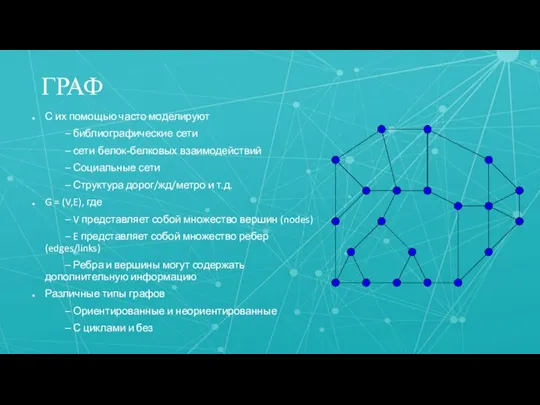
ГРАФ
С их помощью часто моделируют
– библиографические сети
– сети белок-белковых взаимодействий
– Социальные сети
– Структура дорог/жд/метро и т.д.
G = (V,E), где
– V представляет собой множество вершин (nodes)
– E представляет собой множество ребер (edges/links)
– Ребра и вершины могут содержать дополнительную информацию
Различные типы графов
– Ориентированные и неориентированные
– С циклами и без

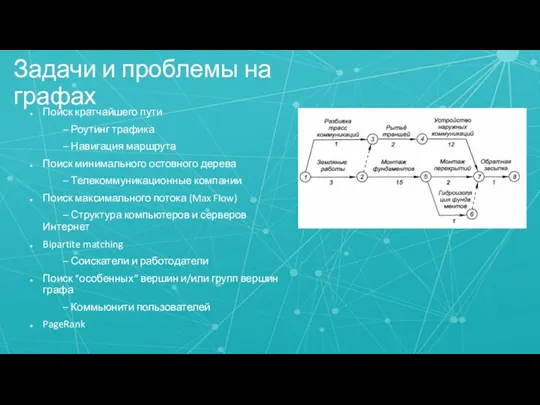
Задачи и проблемы на графах
Поиск кратчайшего пути
– Роутинг трафика
– Навигация маршрута
Поиск минимального остовного дерева
– Телекоммуникационные компании
Поиск максимального потока (Max Flow)
– Структура компьютеров и серверов Интернет
Bipartite matching
– Соискатели и работодатели
Поиск “особенных” вершин и/или групп вершин графа
– Коммьюнити пользователей
PageRank

Графы и MapReduce
Большой класс алгоритмов на графах включает
– Выполнение вычислений на каждой ноде
– Обход графа
Ключевые вопросы
– Как представить граф на MapReduce?
– Как обходить граф на MapReduce?

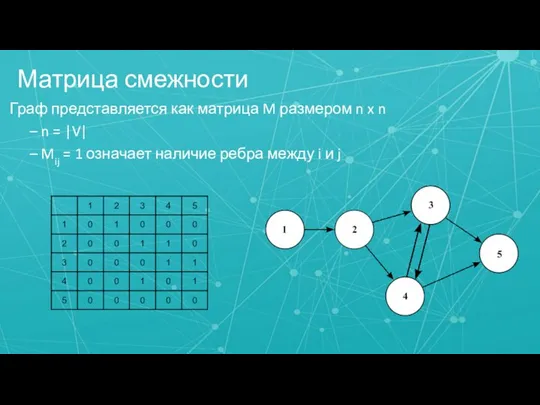
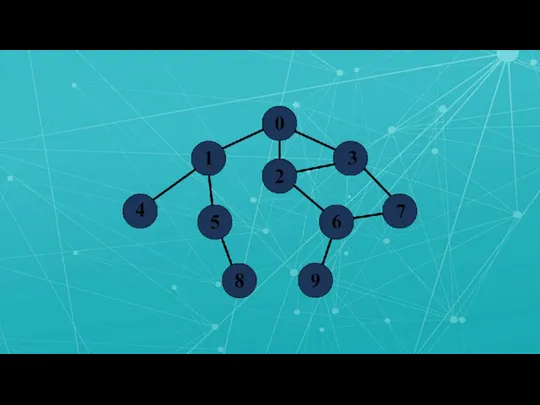
Матрица смежности
Граф представляется как матрица M размером n x n
– n = |V|
– Mij = 1 означает наличие ребра между i и j

Списки смежности
• Берем матрицу смежности и убираем все нули
1: 2
2: 3, 4
3: 4, 5
4: 3, 5
5:

Матрицы смежности
+
– Удобство математических вычислений
– Перемещение по строкам и столбцами соответствует переходу по входящим и исходящим ссылкам
-
– Матрица разреженная, множество лишних нулей
– Расходуется много лишнего места
+
– Намного более компактная реализация
– Легко найти все исходящие ссылки для ноды
-
– Намного сложнее подсчитать входящие ссылки
Списки смежности
Достоинства и недостатки

Задача поиска кратчайшего пути
Найти кратчайший путь от исходной вершины до заданной (или несколько заданных)
Также, кратчайший может означать с наименьшим общим весом всех ребер (Single-Source Shortest Path)
Способы такого обхода:
Алгоритм Дейкстры
MapReduce: параллельный поиск в ширину (Breadth-First Search)

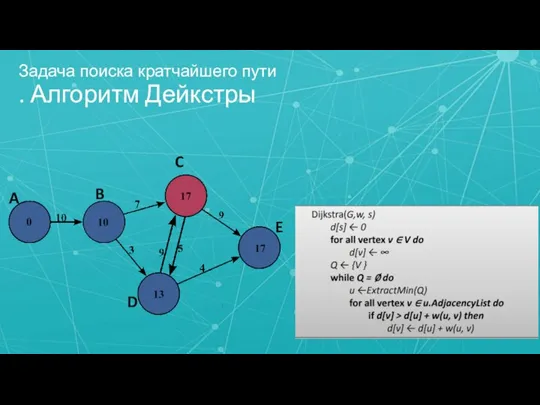
Задача поиска кратчайшего пути
. Алгоритм Дейкстры
C
A
E
B
D

Поиск кратчайшего пути
Рассмотрим простой случай, когда вес всех ребер одинаков и равен единице
Интуитивно:
Определим: в вершину b можно попасть из вершины a только если b есть в списке соседей a, т.е. DistanceTo(b) = 1
Для всех вершин n, достижимых из других множеств M:
DistanceTo(n) = 1 + min(DistanceTo(m), m ∈ M)

Алгоритм breadth-first search

Параллельный BFS
Представление данных:
– Key: вершина n
– Value: d (расстояние от начала), adjacency list (вершины, доступные из n)
– Инициализация: для всех вершин, кроме начальной, d = ∞
Mapper:
– ∀m ∈ adjacency list: emit (m, d + 1)
Sort/Shuffle
– Сгруппировать расстояния по достижимым вершинам
Reducer:
– Выбрать путь с минимальным расстоянием для каждой достижимой вершины
– Дополнительные проверки для отслеживания актуального пути

Параллельный BFS

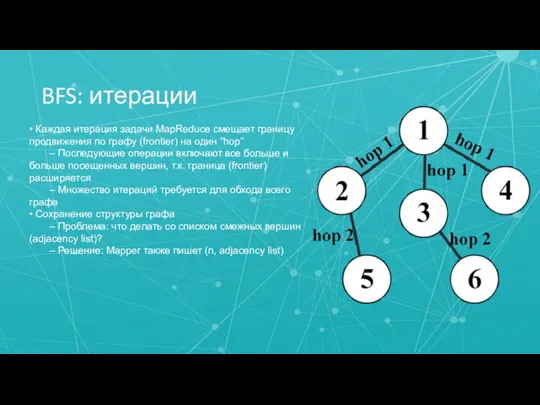
BFS: итерации
• Каждая итерация задачи MapReduce смещает границу продвижения по графу (frontier) на один “hop”
– Последующие операции включают все больше и больше посещенных вершин, т.к. граница (frontier) расширяется
– Множество итераций требуется для обхода всего графа
• Сохранение структуры графа
– Проблема: что делать со списком смежных вершин (adjacency list)?
– Решение: Mapper также пишет (n, adjacency list)

BFS: критерий завершения
Как много итераций нужно для завершения параллельного BFS?
Когда первый раз посетили искомую вершину, значит найден самый короткий путь?
Ответ на вопрос
Равно диаметру графа (наиболее удаленные друг от друга вершины)
Практическая реализация
Внешняя программа-драйвер для проверки оставшихся вершин с дистанцией ∞
Можно использовать счетчики из Hadoop MapReduce

BFS vs Дейкстра
Алгоритм Дейкстры более эффективен
На каждом шаге используются вершины только из пути с минимальным весом
Нужна дополнительная структура данных (priority queue)
MapReduce обходит все пути графа параллельно
Много лишней работы (brute-force подход)
Полезная часть выполняется только на текущей границе обхода

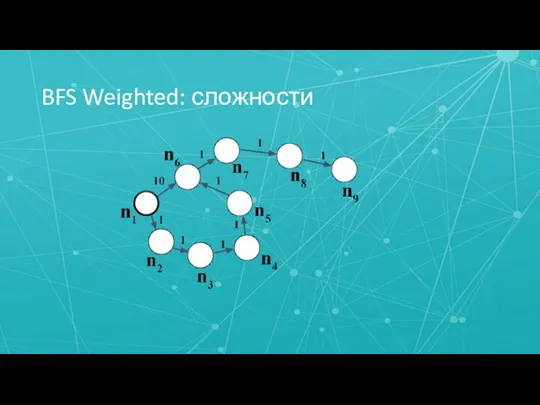
BFS: Weighted Edges
Добавим положительный вес каждому ребру
Простая доработка: добавим вес w для каждого ребра в список смежных вершин
В mapper, emit (m, d + wp) вместо (m, d + 1) для каждой вершины m

BFS Weighted: сложности

BFS Weighted: критерий завершения
Как много итераций нужно для завершения параллельного BFS (взвешенный граф)?
В худшем случае: N – 1
В реальном мире ~ диаметру графа
Практическая реализация
Итерации завершаются, когда минимальный путь у каждой вершины больше не меняется
Для этого можно также использовать счетчики в MapReduce

Графы и MapReduce
Большое количество алгоритмов на графах включает в себя:
Выполнение вычислений, зависимых от особенностей ребер и вершин
Вычисления, основанные на обходе графа
Основной алгоритм:
Представлять графы в виде списка смежности
Производить локальные вычисления на маппере
Передавать промежуточные вычисления по исходящих ребрам, где ключом будет целевая вершина
Выполнять агрегацию на редьюсере по данным из входящих вершин
Повторять итерации до выполнения критерия сходимости, который контролируется внешним драйвером
Передавать структуру графа между итерациями

PageRank
Модель блуждающего веб-серфера
– Пользователь начинает серфинг на случайной веб-странице
– Пользователь произвольно кликает по ссылкам, тем самым перемещаясь от страницы к странице
PageRank
– Характеризует кол-во времени, которое пользователь провел на данной странице
– Математически – это распределение вероятностей посещения страниц
PageRank определяет понятие важности страницы
– Соответствует человеческой интуиции?
– Одна из тысячи фич, которая используется в веб-поиске

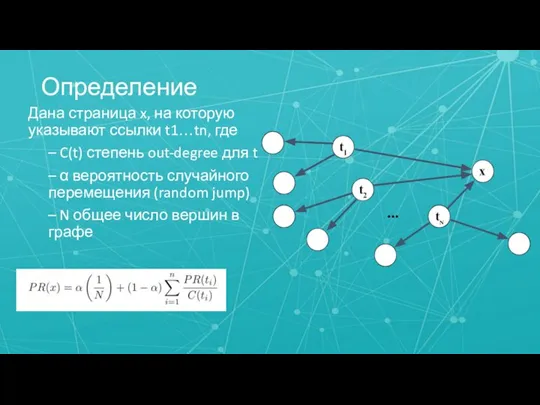
Определение
Дана страница x, на которую указывают ссылки t1…tn, где
– C(t) степень out-degree для t
– α вероятность случайного перемещения (random jump)
– N общее число вершин в графе

Вычисление PageRank без PageRank
PageRank может быть рассчитан итеративно
Примерный алгоритм:
Начать с некоторыми заданными значения PRi
Каждая страница распределяет PRi “кредит” всем страниц, на которые с нее есть ссылки
Каждая страница добавляет весь полученный “кредит” от страниц, которые на нее ссылаются, для подсчета PRi+1
Продолжить итерации пока значения не сойдутся

Упрощения для PageRank
Случайный переход и “подвисшие” вершины
Нет фактора случайного перехода (random jump)
Нет “подвисших” вершин
Затем, добавим сложностей
Зачем нужен случайный переход?
Откуда появляются “подвисшие” вершины?

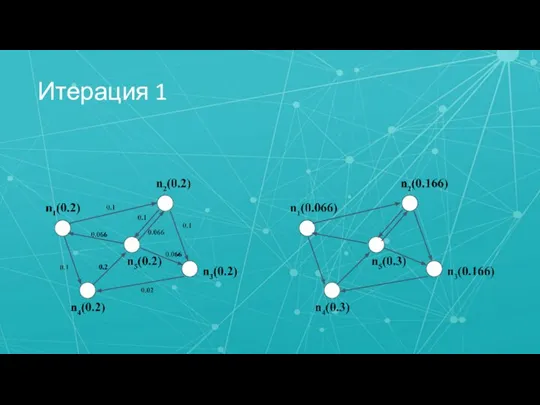
Итерация 1

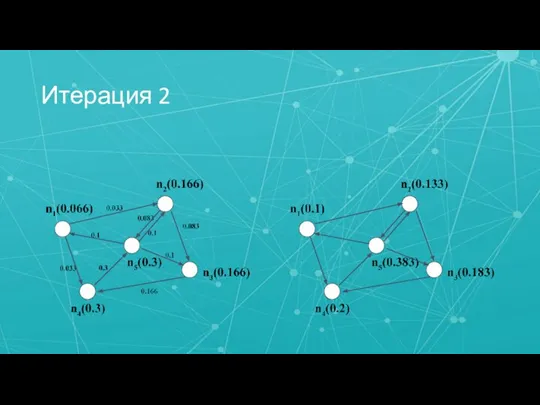
Итерация 2

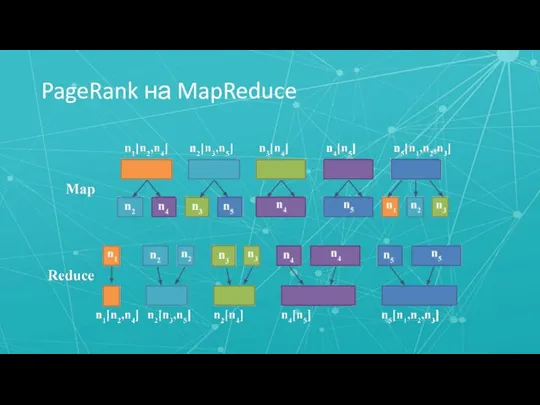
PageRank на MapReduce

Псевдокод на MapReduce

Полный PageRank
Две дополнительные сложности
Как правильно обрабатывать “подвешенные” вершины?
Как правильно определить фактор случайного перехода (random jump)?
Решение :
Второй проход для перераспределения “оставшегося” PageRank и учитывания фактор случайного перехода:
p – значение PageRank полученное “до”, p' – обновленное значение PageRank
N - число вершин графа
m – “оставшийся” PageRank

Критерии сходимости PageRank
Продолжать итерации пока значения PageRank не перестанет изменяться
Фиксированное число итераций