Содержание
- 2. Модель процесса принятия решений Анализ ситуации и формализация исходной проблемы – постановка проблемы, определение целей, отбор
- 3. оптимизация – стремление получить наилучший вариант среди возможных вариантов. Задача оптимизации решается перебором вариантов структуры объекта
- 4. в самом общем виде модель объекта проектирования можно задать в следующем виде: где F – некоторая
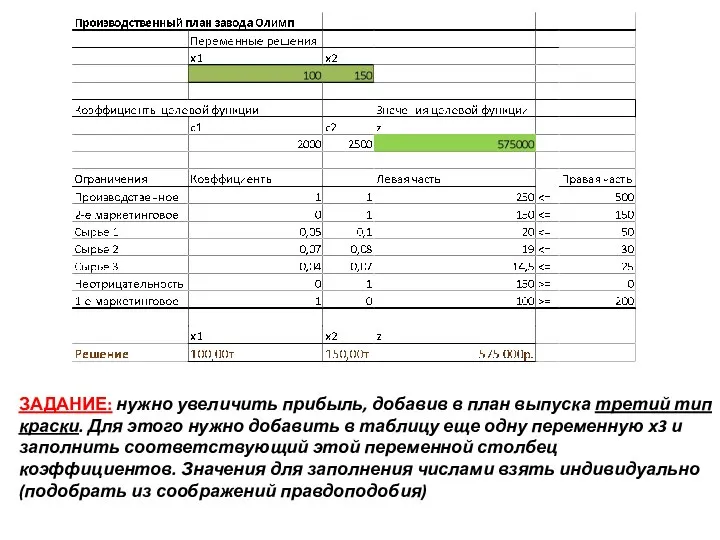
- 5. ФОРМАЛЬНАЯ МОДЕЛЬ ПРИМЕР оптимизировать выпуск краски 2-х видов (А,Б) Дано: краска А приносит прибыль 2000 руб/тонна,
- 6. ЗАДАНИЕ: нужно увеличить прибыль, добавив в план выпуска третий тип краски. Для этого нужно добавить в
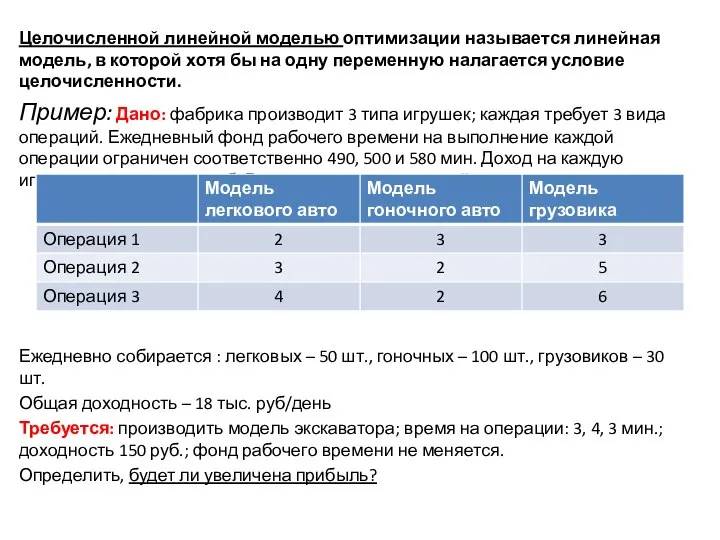
- 7. Целочисленной линейной моделью оптимизации называется линейная модель, в которой хотя бы на одну переменную налагается условие
- 9. Скачать презентацию




 Сообщение по методу Цезаря
Сообщение по методу Цезаря Egov - электронное правительство
Egov - электронное правительство Презентация на тему Файлы и файловая система (8 класс)
Презентация на тему Файлы и файловая система (8 класс)  Компьютерная графика
Компьютерная графика MT_webinar_19.03 (1)
MT_webinar_19.03 (1) Стандартизация в области информационных технологий
Стандартизация в области информационных технологий Microsoft-Office-2010-CZ-Professional-Plus-+-key,-aktivátor
Microsoft-Office-2010-CZ-Professional-Plus-+-key,-aktivátor Проект по благоустройству улиц города
Проект по благоустройству улиц города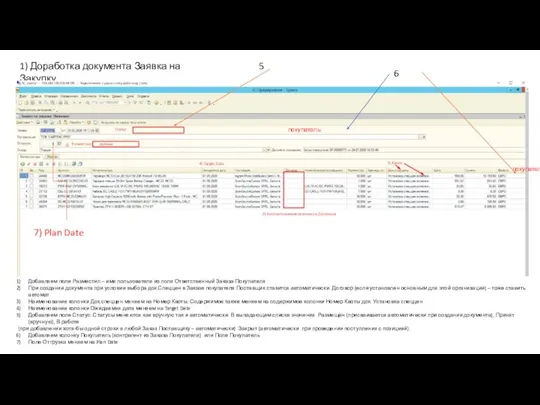 Доработка документа Заявка на Закупку
Доработка документа Заявка на Закупку Мое изобретение
Мое изобретение Федеральная служба по финансовому мониторингу. Регистрация в новом личном кабинете
Федеральная служба по финансовому мониторингу. Регистрация в новом личном кабинете Эволюция ОС
Эволюция ОС Американский национальный институт стандартов
Американский национальный институт стандартов Основы САПР. Введение
Основы САПР. Введение Базы данных и файловые системы. Лекция №1
Базы данных и файловые системы. Лекция №1 Компьютерное моделирование
Компьютерное моделирование 7-1-1 (1)
7-1-1 (1) Construct 2.создаем спиннер
Construct 2.создаем спиннер Типы кабелей и их характеристики. Типы линий и каналов связи
Типы кабелей и их характеристики. Типы линий и каналов связи Работа с векторами и матрицами в MathCad
Работа с векторами и матрицами в MathCad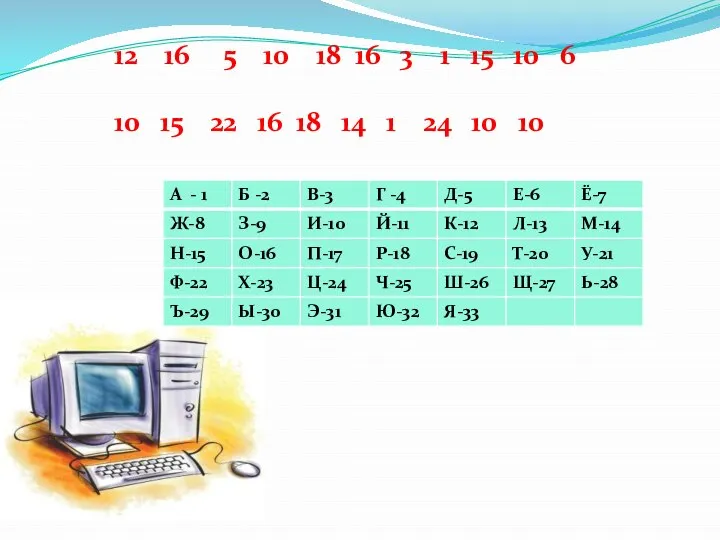 Кодирование информации
Кодирование информации ОС для мобильных устройств. Windows Mobile
ОС для мобильных устройств. Windows Mobile 02_Методологии_разработки_ПО_Agile,_Waterfall,_и_другие
02_Методологии_разработки_ПО_Agile,_Waterfall,_и_другие Концептуальное проектирование БД
Концептуальное проектирование БД Текстовые документы и технологии их создания. Обработка текстовой информации
Текстовые документы и технологии их создания. Обработка текстовой информации Урок информатики
Урок информатики Презентация "Электронные таблицы определение" - скачать презентации по Информатике
Презентация "Электронные таблицы определение" - скачать презентации по Информатике Знакомство с подключением к сети
Знакомство с подключением к сети