Арифметические операции в разных системах счисления

Март 13, 2021

Главная
Информатика
Арифметические операции в разных системах счисления

Содержание

2. Сложение в десятичной системе.
3. Рассмотрим сложение в двоичной системе.
4. Рассмотрим сложение в двоичной системе.
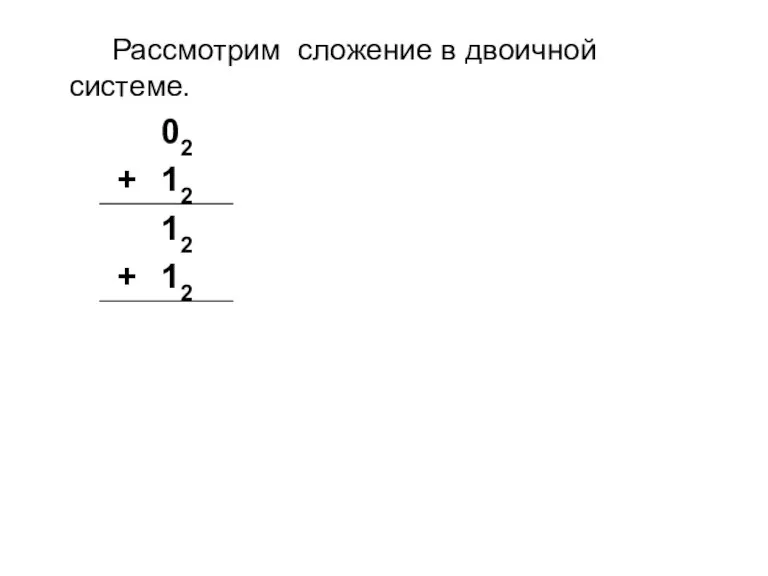
5. Рассмотрим сложение в двоичной системе.
6. Рассмотрим сложение в двоичной системе.
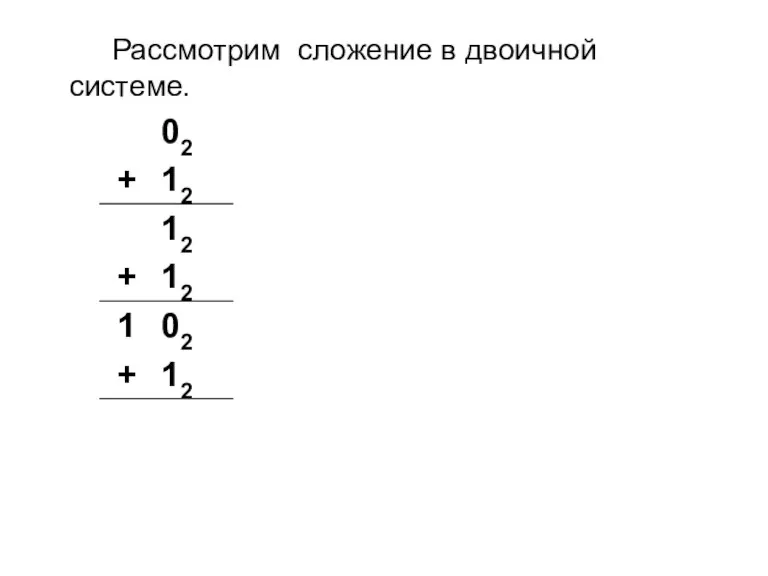
7. Рассмотрим сложение в двоичной системе.
8. Рассмотрим сложение в двоичной системе.
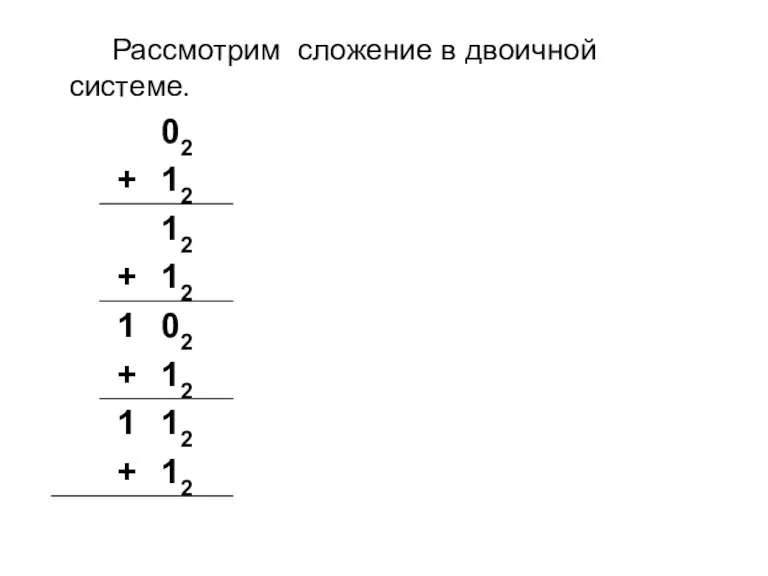
9. Рассмотрим сложение в двоичной системе.
10. Рассмотрим сложение в двоичной системе. При сложении пользуются следующим правилом: 0+1 = 12. Если к 1
11. Пример 1. Сложить 100112 и 110012.
12. Пример 1. Сложить 100112 и 110012.
13. Пример 1. Сложить 100112 и 110012.
14. Пример 1. Сложить 100112 и 110012.
15. Пример 1. Сложить 100112 и 110012.
16. Пример 1. Сложить 100112 и 110012.
17. Пример 1. Сложить 100112 и 110012.
18. Правило сложения чисел в системе счисления с основанием p Записать цифры числа друг под другом, соблюдая
19. Пример 2. Сложить 100113 и 110013.
20. Пример 2. Сложить 100113 и 110013.
21. Пример 3. Сложить 102223 и 210213.
22. Пример 3. Сложить 102223 и 210213.
23. Пример 3. Сложить 102223 и 210213.
24. Пример 3. Сложить 102223 и 210213.
25. Пример 3. Сложить 102223 и 210213.
26. Пример 3. Сложить 102223 и 210213.
27. Пример 3. Сложить 102223 и 210213.
28. Пример 4. Сложить 356278 и 250218.
29. Пример 4. Сложить 356278 и 250218.
30. Пример 4. Сложить 356278 и 250218.
31. Пример 4. Сложить 356278 и 250218.
32. Пример 4. Сложить 356278 и 250218.
33. Пример 5. Сложить ADC2716 и 25EF116.
34. Пример 5. Сложить ADC2716 и 25EF116.
35. Пример 5. Сложить ADC2716 и 25EF116.
36. Пример 5. Сложить ADC2716 и 25EF116.
37. Пример 5. Сложить ADC2716 и 25EF116.
38. Сложение чисел с разным основанием Для того, чтобы сложить два числа с разными основаниями систем счисления,
39. Пример 6. Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.
40. Пример 6. Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.
41. Пример 6. Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.
42. Пример 6. Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.
43. Пример 6. Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.
44. Пример 6. Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.
45. Пример 7. Сложить AD16 и 2518. Результат представить в двоичной системе счисления.
46. Правило вычитания чисел в системе счисления с основанием p Записать цифры числа друг под другом, соблюдая
47. Пример 8. Найти разность чисел 110112 и 11012.
48. Пример 8. Найти разность чисел 110112 и 11012.
49. Пример 8. Найти разность чисел 110112 и 11012.
50. Пример 8. Найти разность чисел 110112 и 11012.
51. Пример 8. Найти разность чисел 110112 и 11012.
52. Пример 9. Найти разность чисел ADC2716 и 25EF116.
53. Пример 9. Найти разность чисел ADC2716 и 25EF116.
54. Пример 9. Найти разность чисел ADC2716 и 25EF116.
55. Пример 9. Найти разность чисел ADC2716 и 25EF116.
56. Пример 9. Найти разность чисел ADC2716 и 25EF116.
57. Пример 9. Найти разность чисел ADC2716 и 25EF116.
58. Задание Чему равна сумма чисел X= 438 и Y=568? Чему равна сумма чисел X= 4316 и
60. Скачать презентацию

Сложение в десятичной системе.

Рассмотрим сложение в двоичной системе.

Рассмотрим сложение в двоичной системе.
При сложении пользуются следующим правилом:
0+1 = 12.
Если к

1 прибавить 1, то получим 2, но цифры 2 нет в двоичной системе, поэтому в складываемый разряд ставим 0, а 1 переносим в следующий разряд.
1+1 = 102

Пример 1.
Сложить 100112 и 110012.

Правило сложения чисел в системе счисления с основанием p
Записать цифры числа друг

под другом, соблюдая разрядность чисел.
Начиная с младшего разряда складывать значения цифр, предварительно переведя их в десятичную систему.
Если сумма значений цифр какого-то разряда превышает основание системы счисления P, то в данный разряд записывается число, равное остатку от деления этой суммы на основание системы P. (или разности данной суммы и основания системы счисления P).
В следующий разряд добавляется единица.

Слайд 19

Пример 2.
Сложить 100113 и 110013.

Слайд 20

Пример 2.
Сложить 100113 и 110013.

Слайд 21

Пример 3.
Сложить 102223 и 210213.

Слайд 22

Пример 3.
Сложить 102223 и 210213.

Слайд 23

Пример 3.
Сложить 102223 и 210213.

Слайд 24

Пример 3.
Сложить 102223 и 210213.

Слайд 25

Пример 3.
Сложить 102223 и 210213.

Слайд 26

Пример 3.
Сложить 102223 и 210213.

Слайд 27

Пример 3.
Сложить 102223 и 210213.

Слайд 28

Пример 4.
Сложить 356278 и 250218.

Слайд 29

Пример 4.
Сложить 356278 и 250218.

Слайд 30

Пример 4.
Сложить 356278 и 250218.

Слайд 31

Пример 4.
Сложить 356278 и 250218.

Слайд 32

Пример 4.
Сложить 356278 и 250218.

Слайд 33

Пример 5.
Сложить ADC2716 и 25EF116.

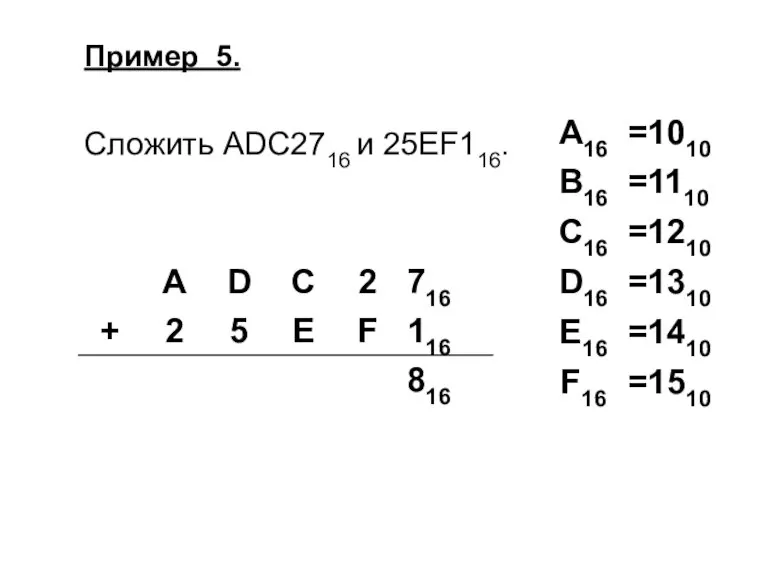
Слайд 34

Пример 5.
Сложить ADC2716 и 25EF116.

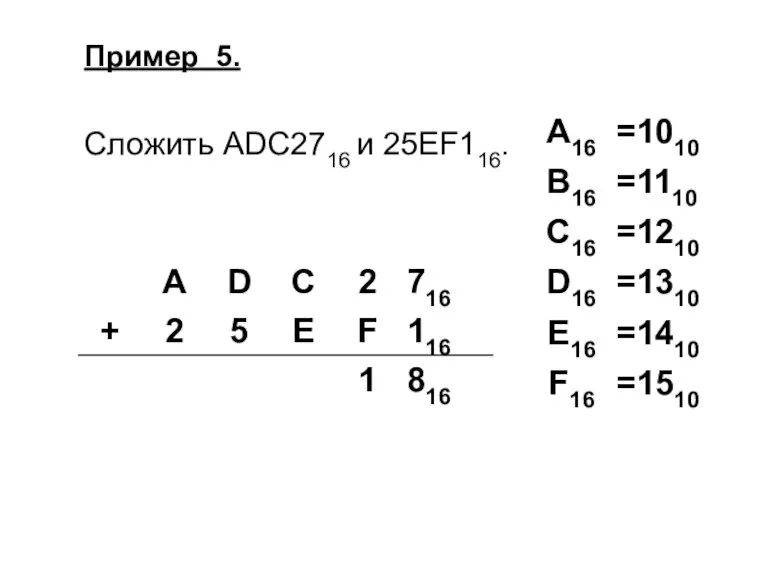
Слайд 35

Пример 5.
Сложить ADC2716 и 25EF116.

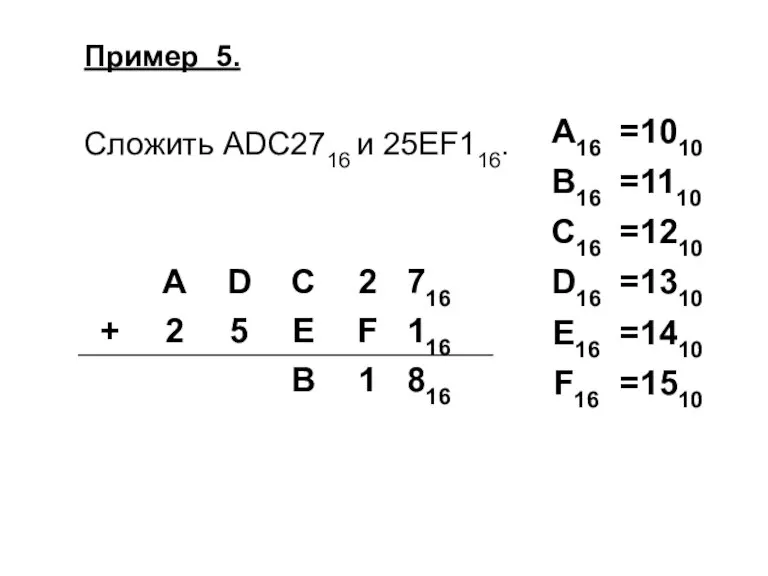
Слайд 36

Пример 5.
Сложить ADC2716 и 25EF116.

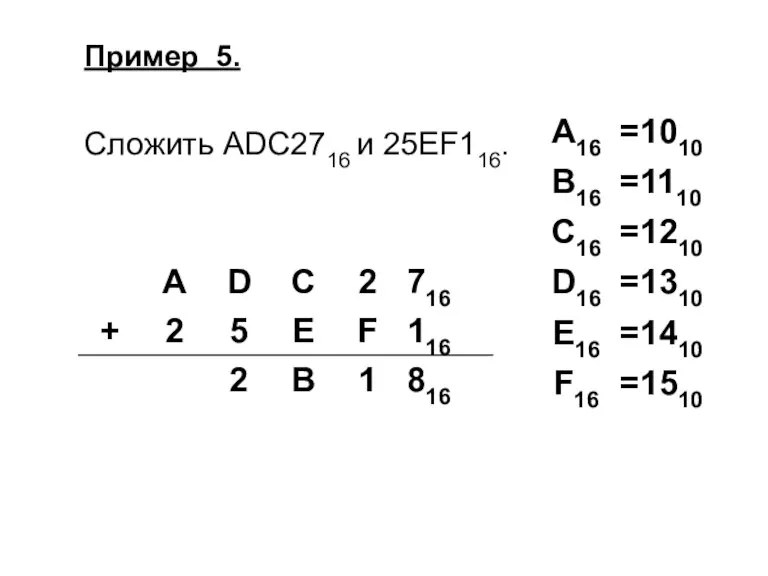
Слайд 37

Пример 5.
Сложить ADC2716 и 25EF116.

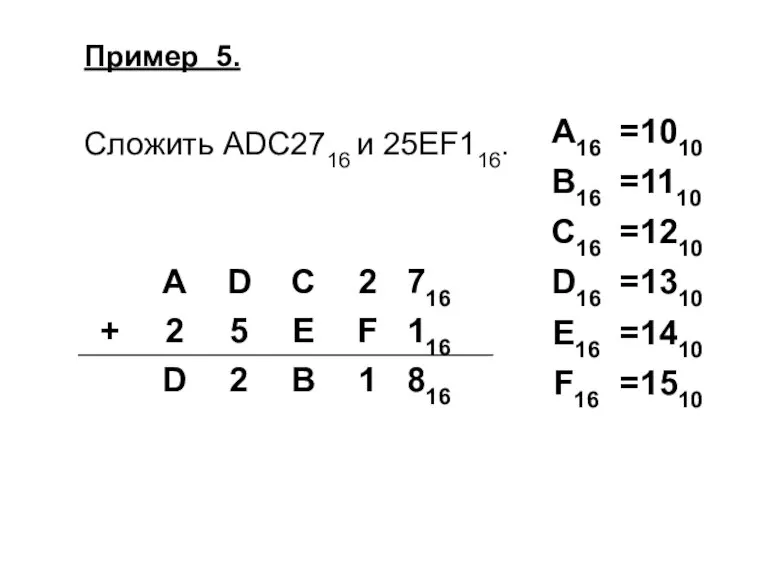
Слайд 38

Сложение чисел с разным основанием
Для того, чтобы сложить два числа с разными

основаниями систем счисления, их надо перевести в одну (удобную для вас) систему счисления и выполнить сложение.
Результат представить в требуемой в задании системе счисления.

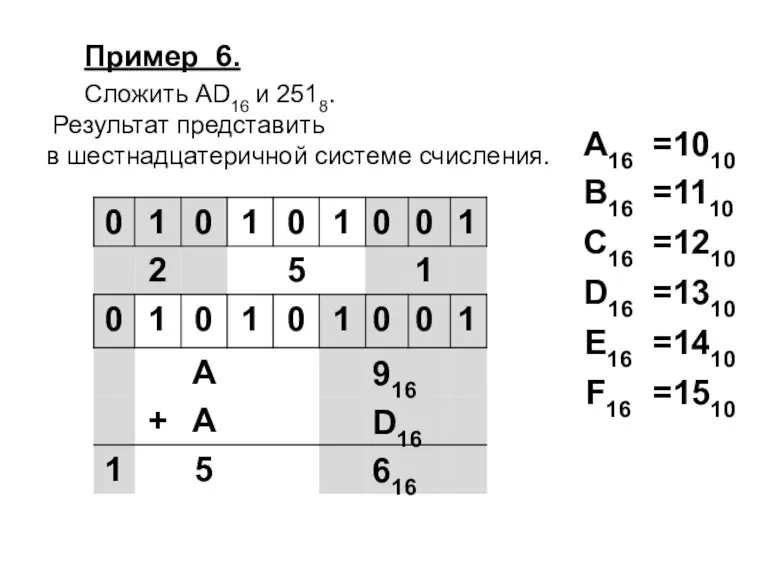
Слайд 39

Пример 6.
Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.

Слайд 40

Пример 6.
Сложить AD16 и 2518. Результат представить в
шестнадцатеричной системе счисления.

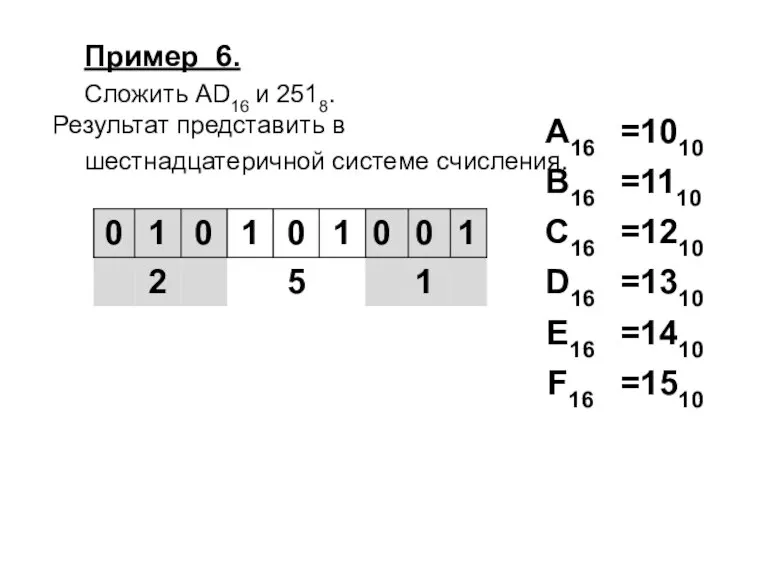
Слайд 41

Пример 6.
Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.

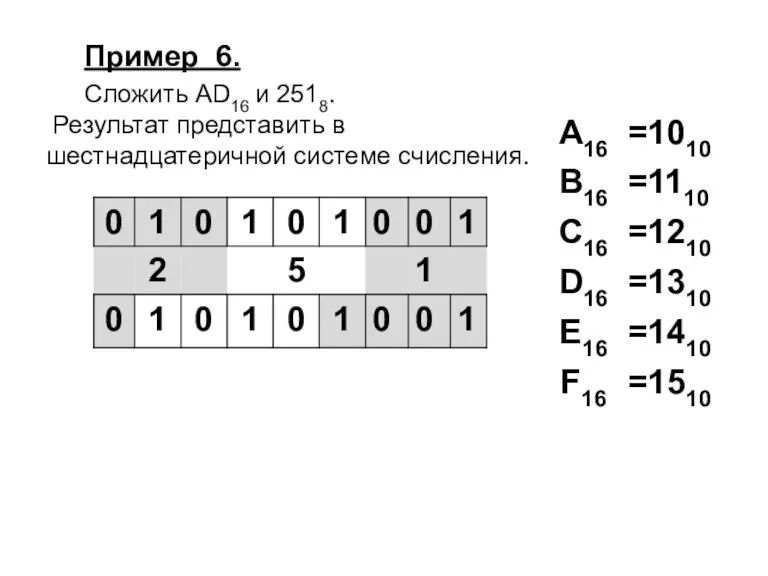
Слайд 42

Пример 6.
Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.

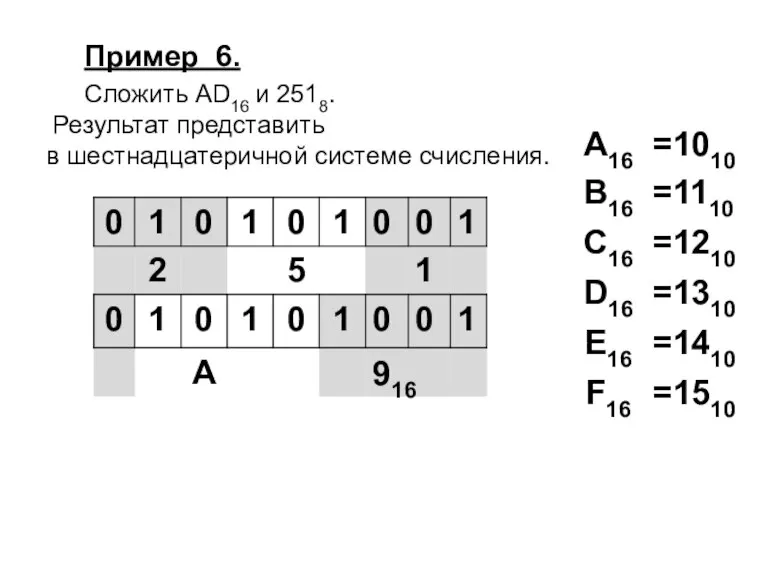
Слайд 43

Пример 6.
Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.

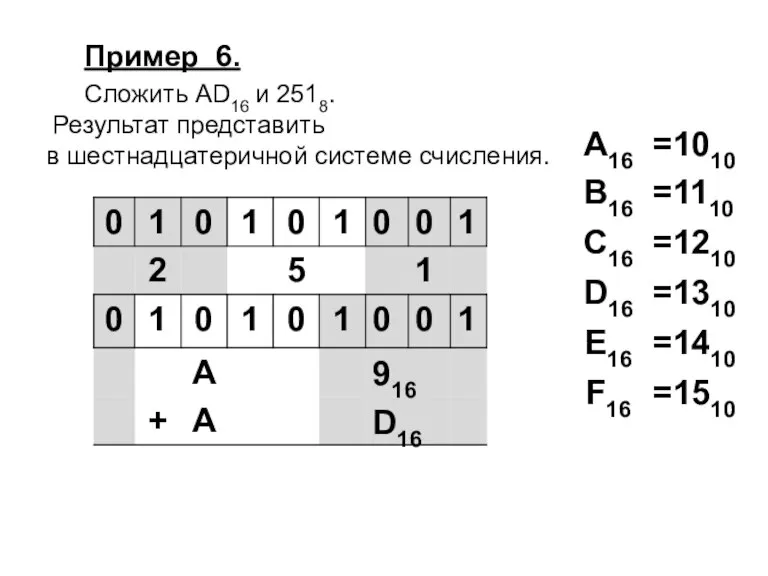
Слайд 44

Пример 6.
Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.

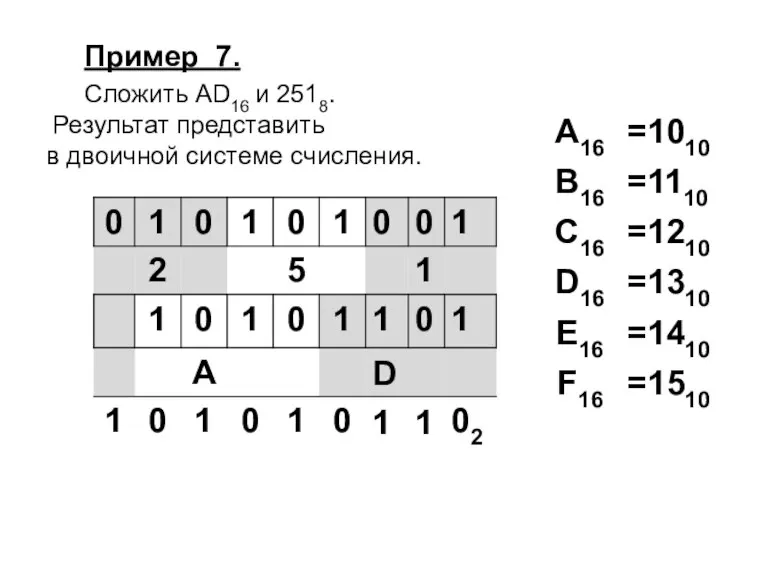
Слайд 45

Пример 7.
Сложить AD16 и 2518. Результат представить в двоичной системе счисления.

Слайд 46

Правило вычитания чисел в системе счисления с основанием p
Записать цифры числа друг

под другом, соблюдая разрядность чисел.
Начиная с младшего разряда вычитать значения цифр, предварительно переведя их в десятичную систему.
Если в каком-то разряде уменьшаемое число меньше вычитаемого, то необходимо занять единицу из следующего разряда. При этом нужно помнить, что значение этой единицы равно основанию системы счисления P.

Слайд 47

Пример 8.
Найти разность чисел 110112 и 11012.

Слайд 48

Пример 8.
Найти разность чисел 110112 и 11012.

Слайд 49

Пример 8.
Найти разность чисел 110112 и 11012.

Слайд 50

Пример 8.
Найти разность чисел 110112 и 11012.

Слайд 51

Пример 8.
Найти разность чисел 110112 и 11012.

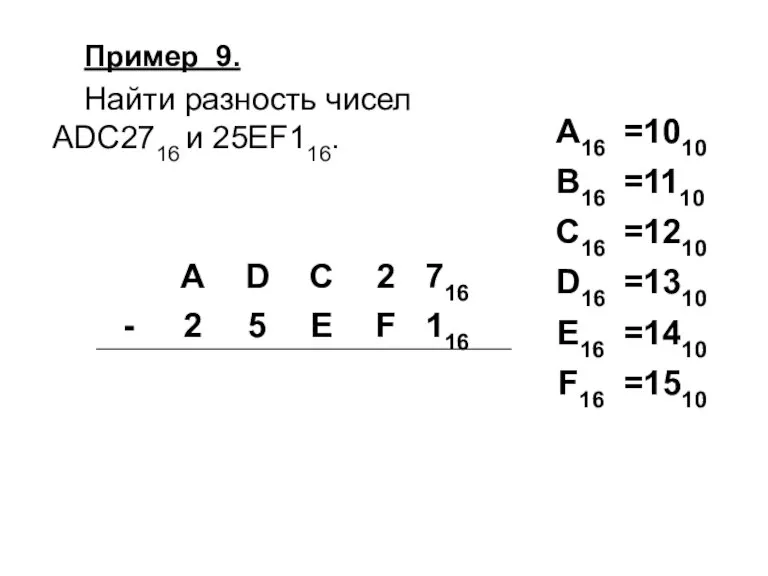
Слайд 52

Пример 9.
Найти разность чисел ADC2716 и 25EF116.

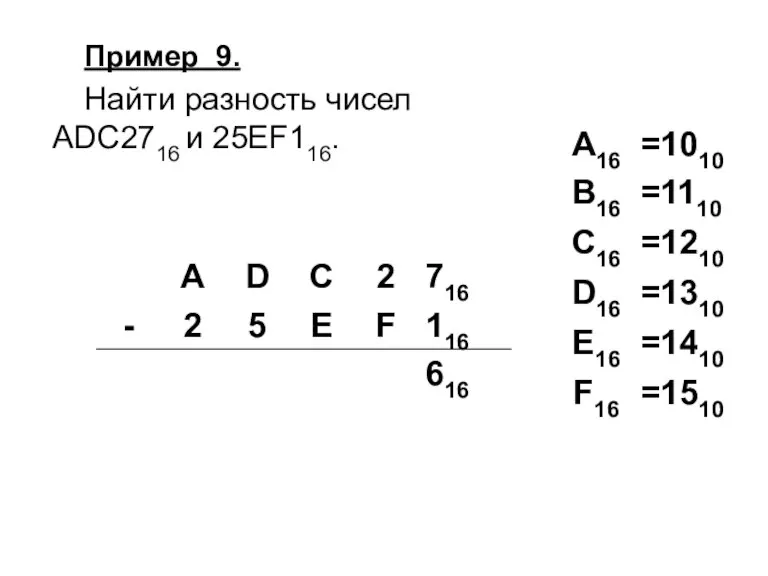
Слайд 53

Пример 9.
Найти разность чисел ADC2716 и 25EF116.

Слайд 54

Пример 9.
Найти разность чисел ADC2716 и 25EF116.

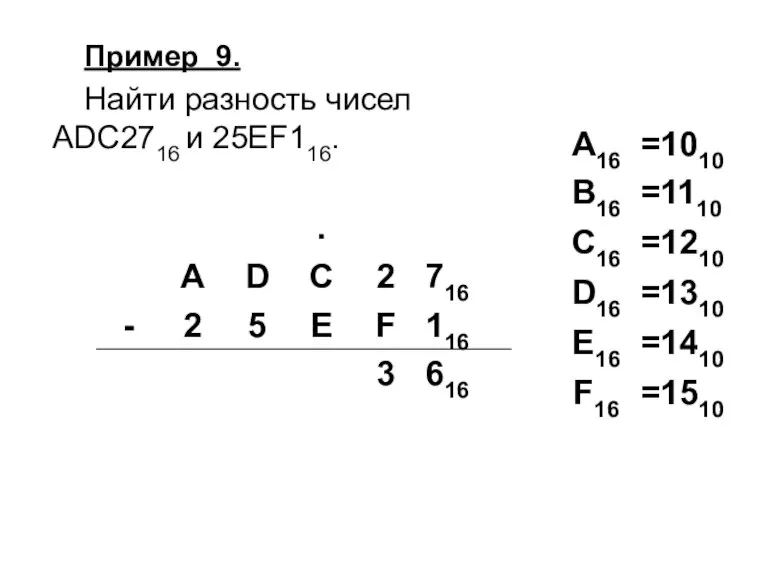
Слайд 55

Пример 9.
Найти разность чисел ADC2716 и 25EF116.

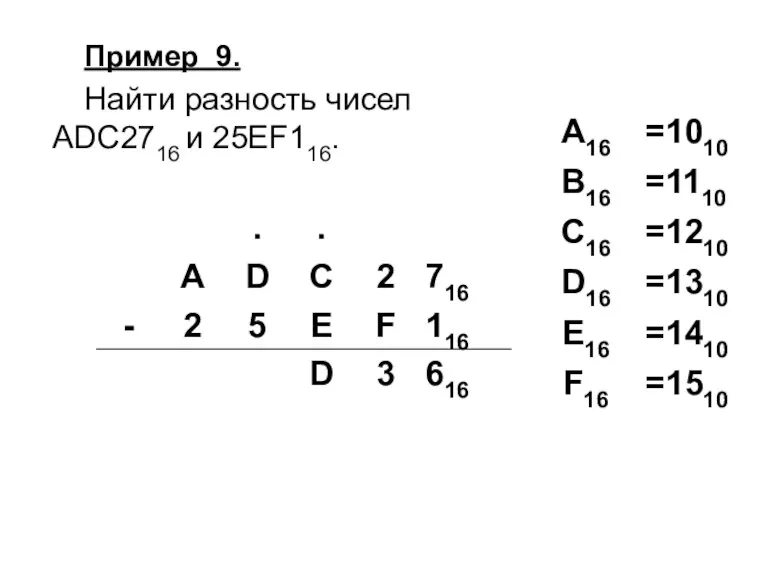
Слайд 56

Пример 9.
Найти разность чисел ADC2716 и 25EF116.

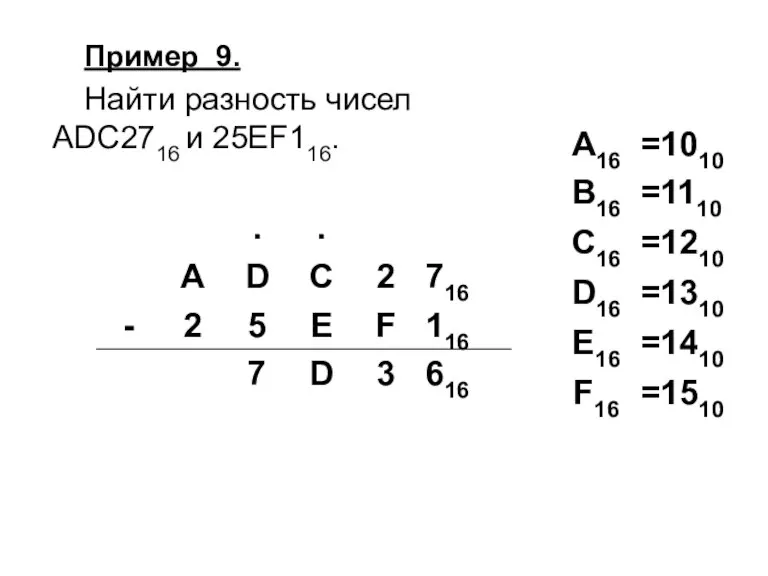
Слайд 57

Пример 9.
Найти разность чисел ADC2716 и 25EF116.

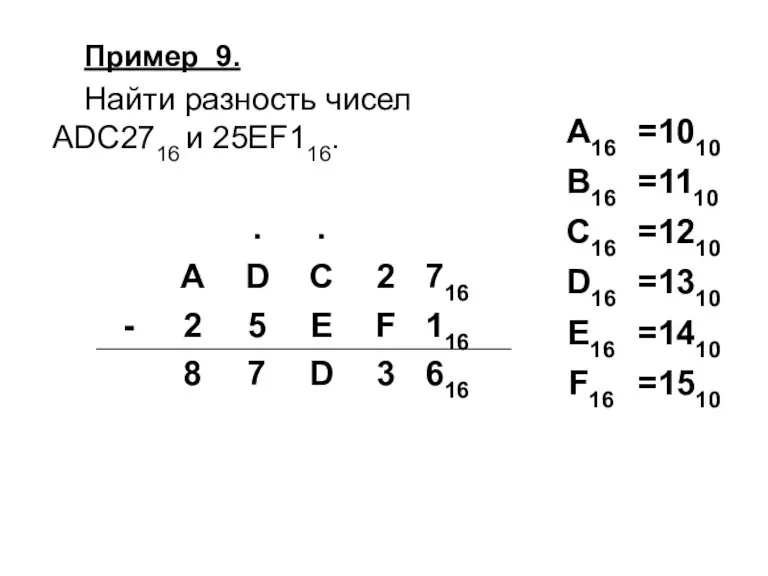
Слайд 58

Задание
Чему равна сумма чисел X= 438 и Y=568?
Чему равна сумма

чисел X= 4316 и Y=5616?
Чему равна сумма чисел X= 438 и Y=5616? Результат выразить последовательно в двоичной, восьмеричной и шестнадцатеричной системах счисления.
Чему равна сумма чисел X= 11100112 и Y=10010012?
Чему равна сумма чисел X= 558 и Y=AE116? Результат выразить в шестнадцатеричной системе счисления.
Чему равно значение выражения 1016 + 108 • 102 в двоичной системе счисления?