Арифметические основы организации ЭВМ

Сложение и вычитание чисел с фиксированной запятой
Сложение и вычитание представляют пару операций «типа сложения», т.е. алгебраическое сложение, которое, в свою очередь, можно понимать как сложение чисел со знаком, заданных в обратном или дополнительном коде.
Вычитание может выполняться непосредственно (с использованием, например, специальных операционных элементов – вычитателей) или косвенно, путем сведения его к сложению:
Z : = X – Y = X + (–Y)

Сложение и вычитание чисел с фиксированной запятой
В последнем случае достаточно, как видно, изменить знак второго операнда. Если операнды (и результат) представлены в дополнительном коде, изменение знака производится путем инверсии всех разрядов и добавления 1 в младшем разряде. Например,
Y = 5 ~ 0.1012
–Y = –5 ~ 1 0102
+ ____1
1.0112 = (–5)доп,
и наоборот,
Y = –5 ~ 1.0112
–Y = 5 ~ 0 1002
+ ____1
0.1012 = (5)доп.

Сложение и вычитание чисел с фиксированной запятой
Правила алгебраического сложения чисел в обратном и дополнительном кодах тривиальны: обратные или дополнительные коды операндов суммируются как обыкновенные числа без знака, возможная единица переноса из знакового разряда (старшего знакового разряда, если код модифицированный) циклически переносится в младший разряд для второго суммирования (обратный код) или отбрасывается (дополнительный код).
« + » – знак операции сложения с циклическим переносом (Пример 1).

Сложение и вычитание чисел с фиксированной запятой
Пример 1.
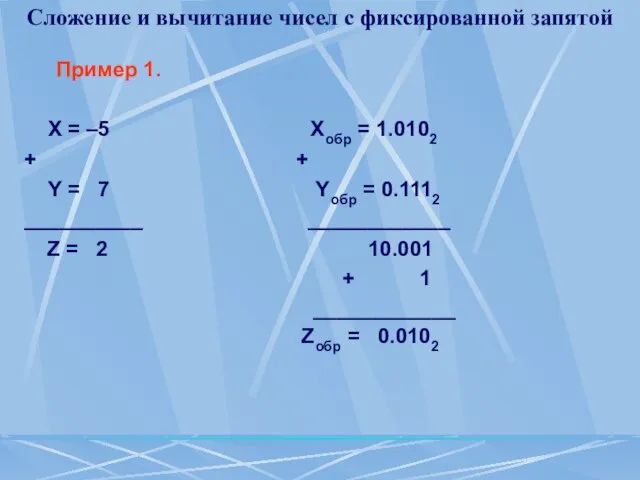
Х = –5 Xобр = 1.0102
+ +
Y = 7 Yобр = 0.1112
__________ ____________
Z = 2 10.001
+ 1
____________
Zобр = 0.0102

Сложение и вычитание чисел с фиксированной запятой
Пример 2.
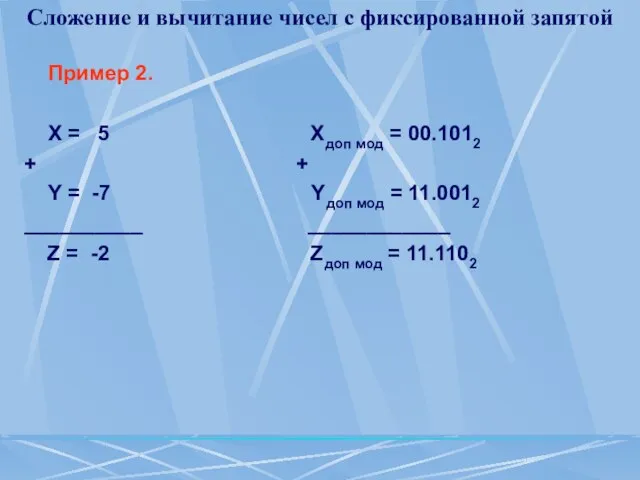
Х = 5 Xдоп мод = 00.1012
+ +
Y = -7 Yдоп мод = 11.0012
__________ ____________
Z = -2 Zдоп мод = 11.1102

Сложение и вычитание чисел с фиксированной запятой
Вообще, при сложении чисел с разными знаками в дополнительном коде отсутствие переноса свидетельствует об отрицательном результате (как в Примере 2), а наличие – о результате положительном или нулевом (Пример 3).
Пример 3.
Х = 5 Xдоп = 0.1012
+ +
Y = -5 Yдоп = 1.0112
__________ ____________
Z = 0 Zдоп = 10.0102
рвых = 1

Сложение и вычитание чисел с фиксированной запятой
В обратном коде отсутствие выходного переноса свидетельствует о неположительном результате (Пример 4), а наличие его – о результате положительном (Пример 1).
Пример 4.
Х = 5 Xобр = 0.1012
+ +
Y = -5 Yдоп = 1.0102
__________ ____________
Z = 0 Zобр = 1.1112 = (- 0)обр
рвых = 0

Сложение и вычитание чисел с фиксированной запятой
Обнаружение переполнения разрядной сетки при сложении может производиться несколькими способами.
Самый простой способ – использование модифицированного кода (с двумя знаковыми разрядами).
Старший знаковый разряд даже при переполнении сохраняет информацию о знаке результата («Разряд знака»).
Младший – «Разряд переполнения». Комбинация знаков при «положительном» переполнении – 01,
при «отрицательном» – 10.

Сложение и вычитание чисел с фиксированной запятой
Пример 5.
Х = 3 Xдоп мод = 00.0112
+ +
Y = 6 Yдоп мод = 00.1102
__________ ____________
Z = 9 > 7 Zдоп мод ~ 01.0012 (положительное
переполнение)
Пример 6.
х = - 3 Xдоп мод = 11.1012
+ +
у = - 6 Yдоп мод = 11.0102
__________ ____________
z = - 9 < 8 Zдоп мод ~ 10.1112 (отрицательное
переполнение)

Сложение и вычитание чисел с фиксированной запятой
В примере 6 указано граничное значение (- 8), которое может быть представлено без переполнения:
(-8) доп мод = 11.0002
Недостаток способа модифицированного кода — расширение разрядной сетки на один разряд.

Сложение и вычитание чисел с фиксированной запятой
Второй способ обнаружения переполнения - сравнение переносов в знаковый разряд и из знакового разряда. Переполнение - при несовпадении этих переносов. Фактически здесь тоже «задействован» модифицированный дополнительный код.
Случай А. Неотрицательные операнды.

Сложение и вычитание чисел с фиксированной запятой
Правило сравнения переносов дает значение признака переполнения:
φр = 0 ⊕ X = X
(переполнение при X = 1).
Слева от штриховой черты показаны значения воображаемого модифицированного дополнительного кода. Правило этого способа дает такое же значение признака переполнения:
φм = 0 ⊕ X = X

Сложение и вычитание чисел с фиксированной запятой
Случай В. Отрицательные операнды.
Здесь тоже φр = φм = 1 ⊕ X = X
(переполнение может быть только отрицательное - при отсутствии переноса из старшего цифрового разряда).

Сложение и вычитание чисел с фиксированной запятой
Случай С. Операнды имеют разные знаки
Оба признака переполнения снова совпадают, они имеют нулевые значения (переполнение в принципе невозможно):
φр = Х ⊕ X = 0
φм = Х ⊕ X = 0