Содержание
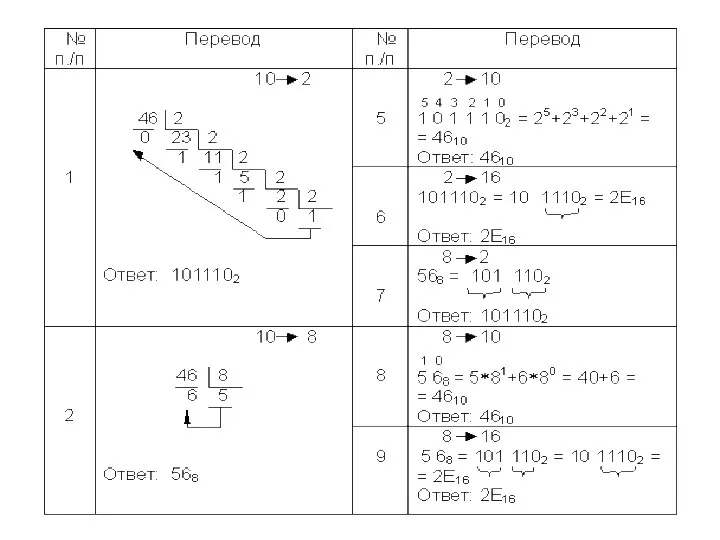
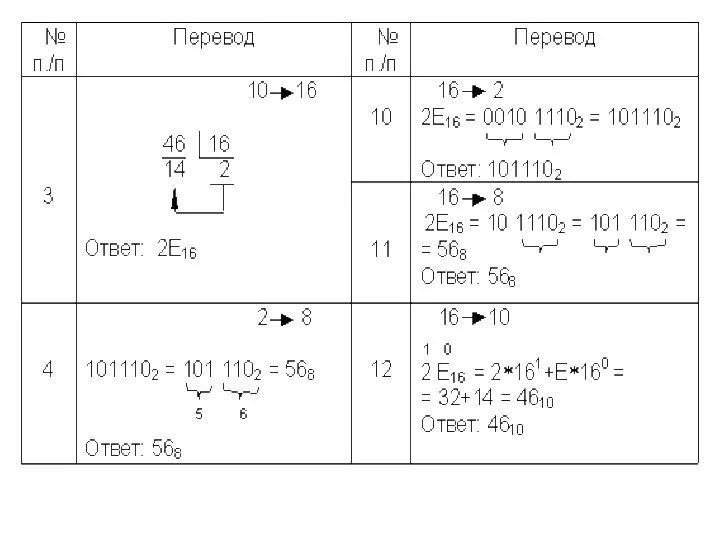
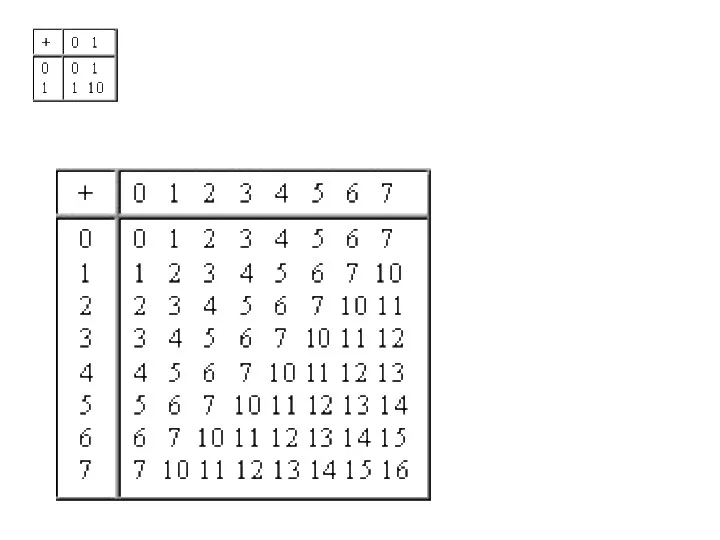
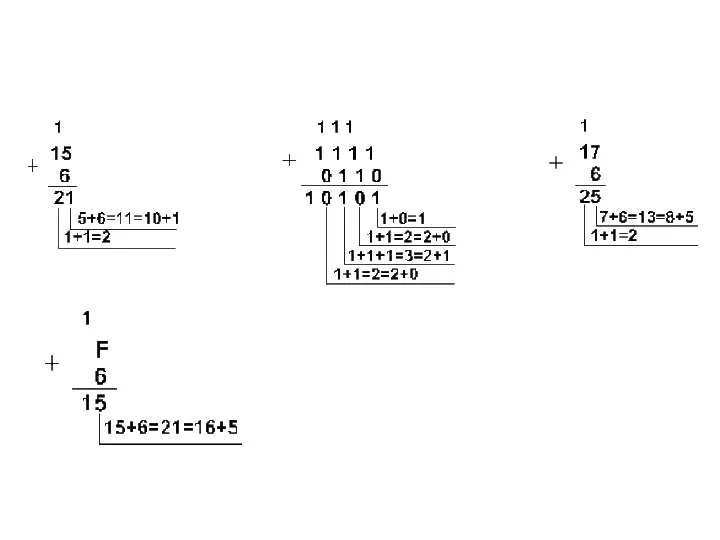
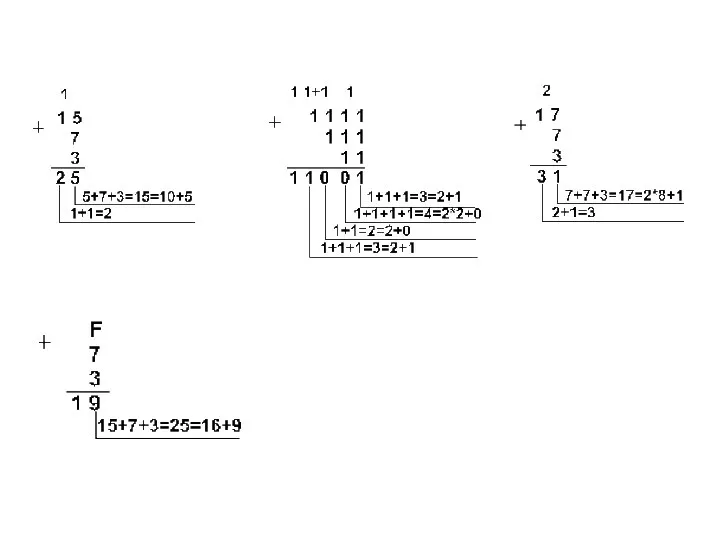
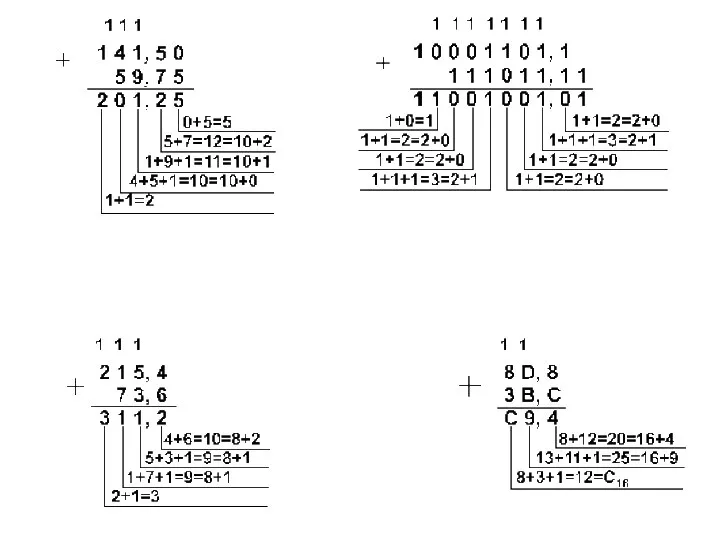
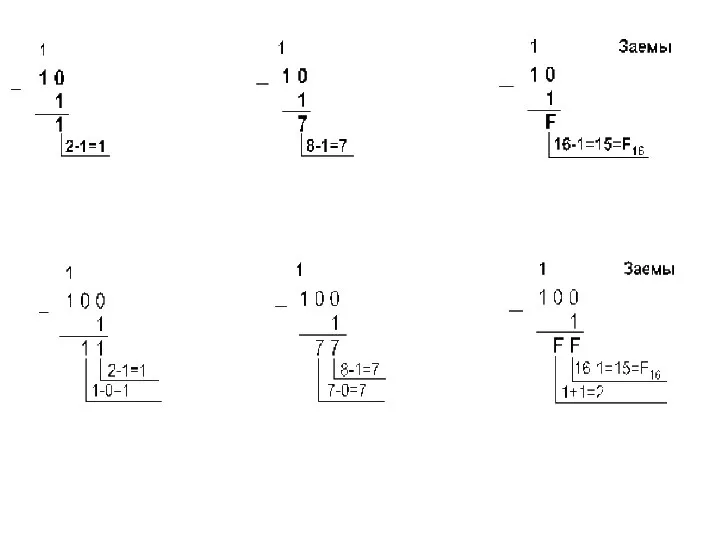
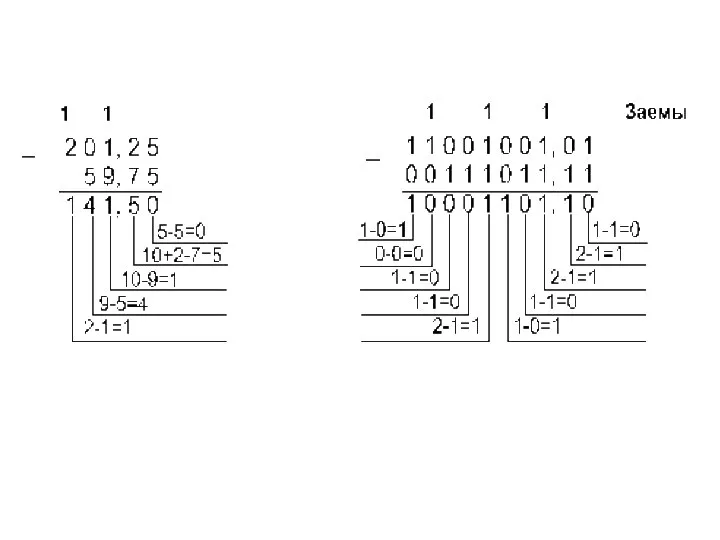
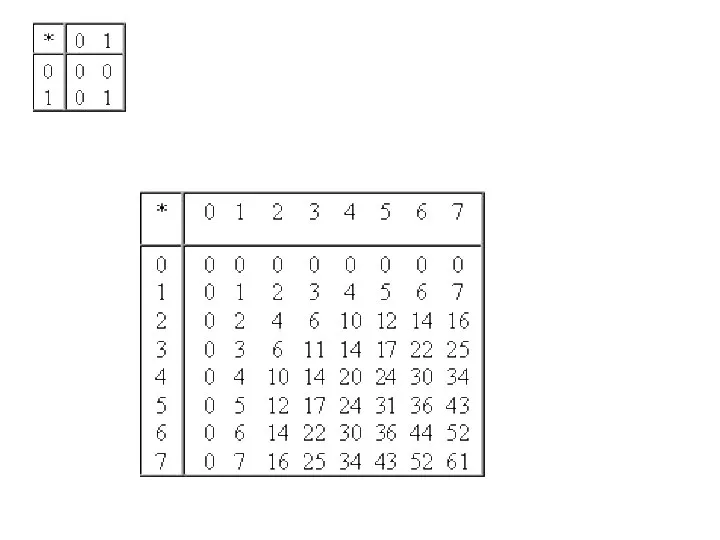
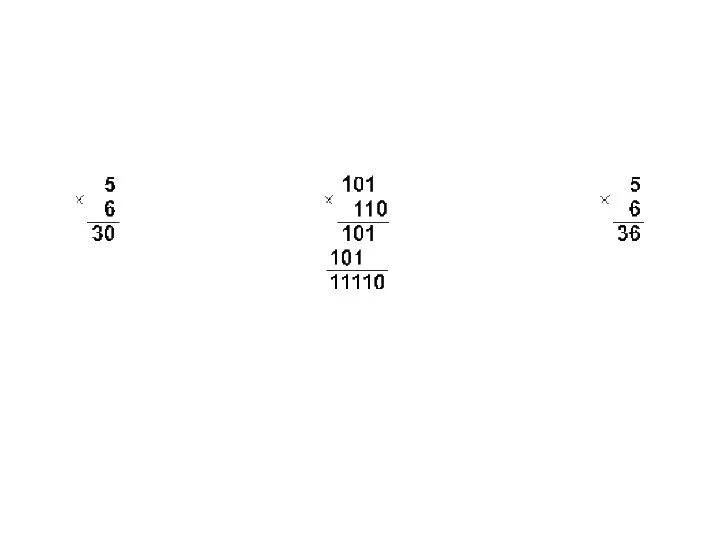
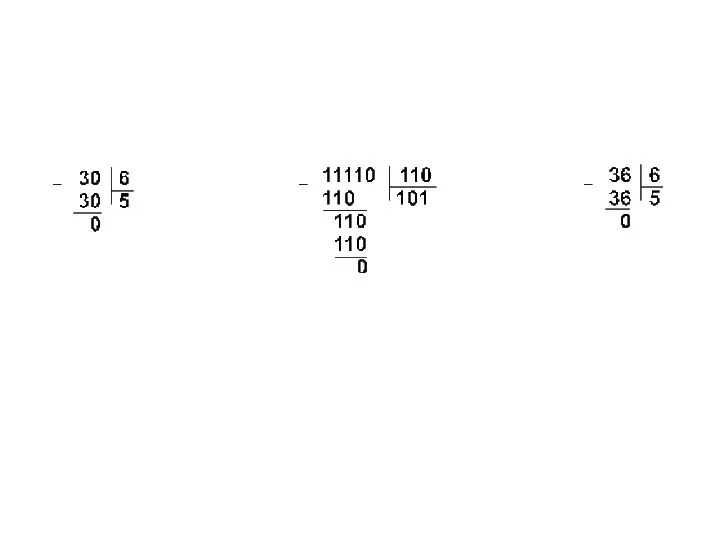
- 34. Сложение чисел в форме с фиксированной запятой Перевести слагаемые в двоичную систему счисления. Разрядность. Перевести слагаемы
- 35. Сложение в обратном коде
- 36. Сложение в дополнительном коде
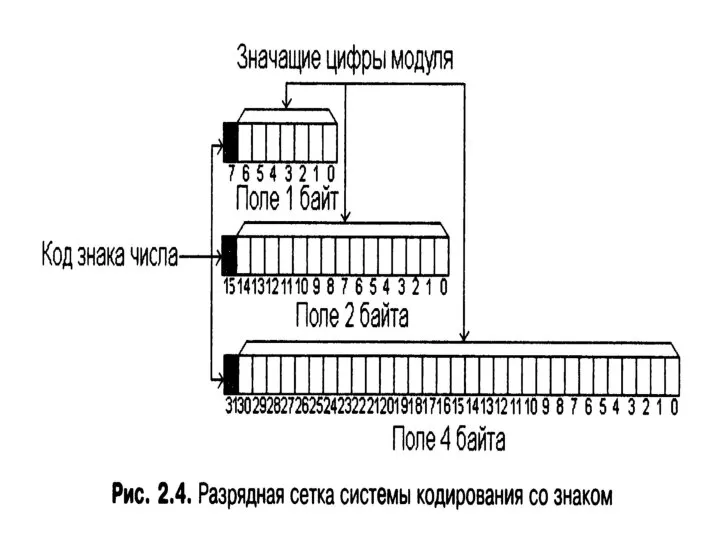
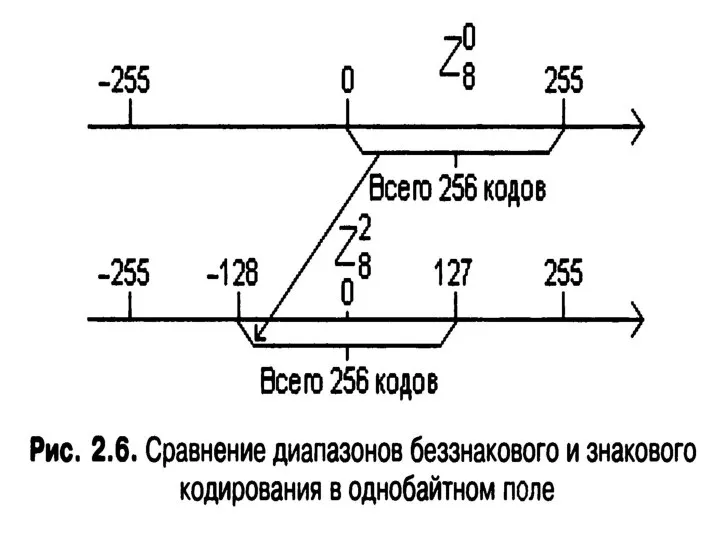
- 37. Правильный результат
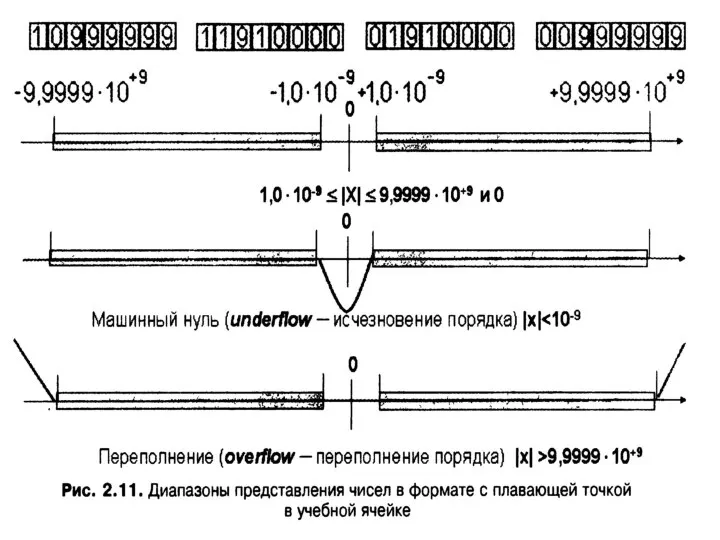
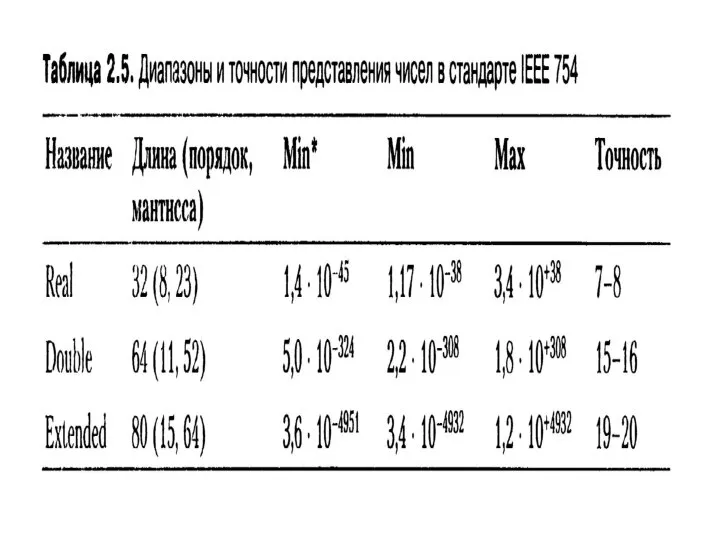
- 38. Сложение чисел в форме с плавающей запятой (нормальная форма) 1. Записать слагаемые в прямом коде. 2.
- 39. Пример Х = 0,1101 × 10 110; Y = 0,1011 × 10 010 Порядок числа Y(010(2)
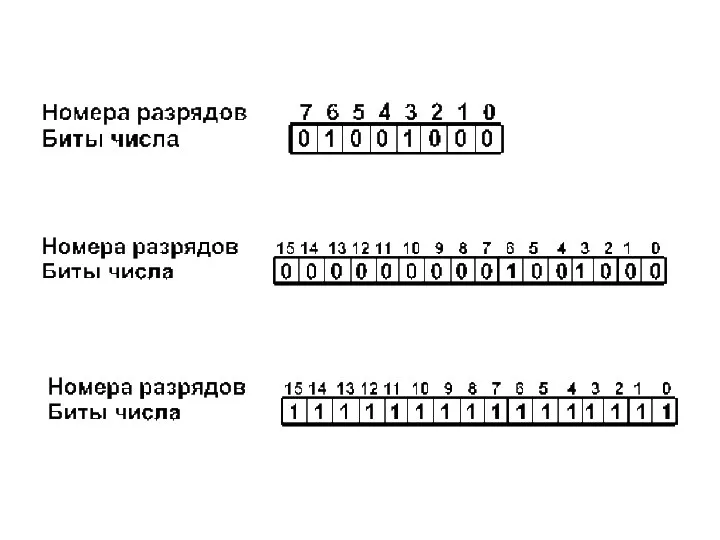
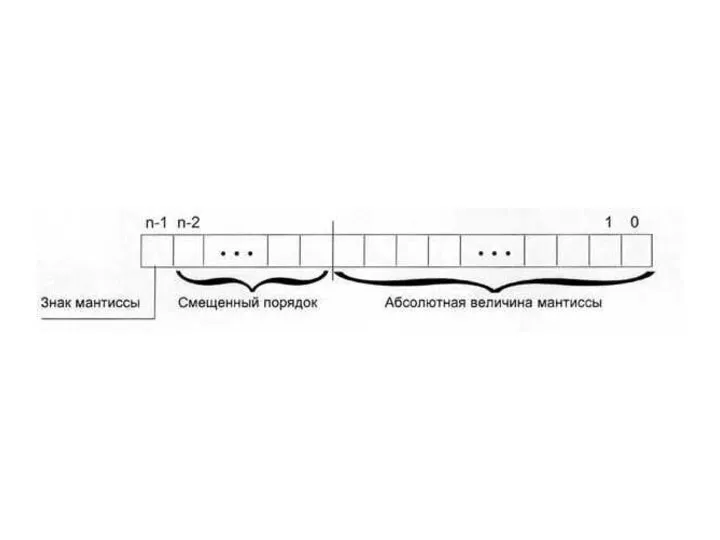
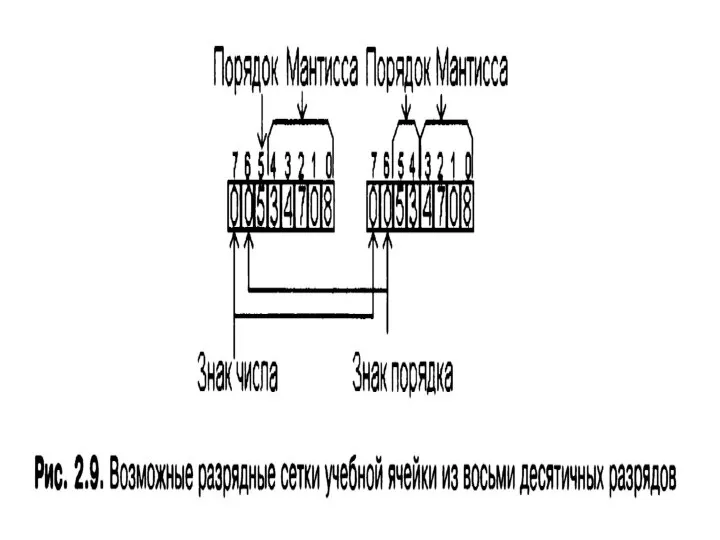
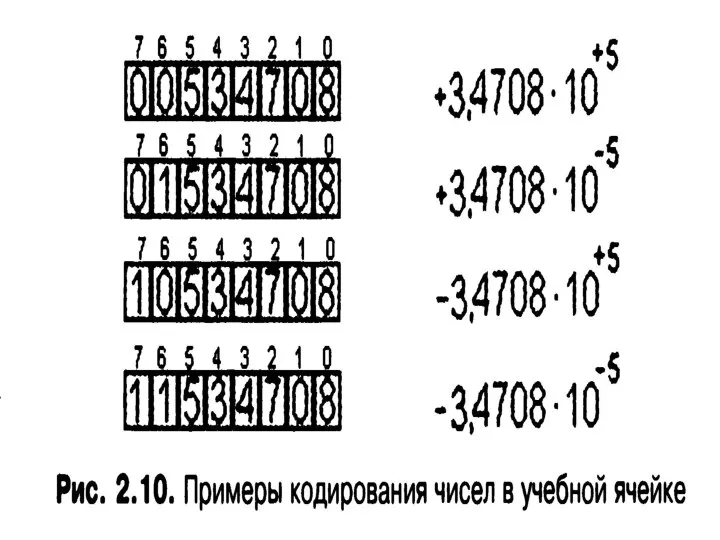
- 40. Запись в учебной ячейке ЭВМ знак числа мантисса знак порядка порядок -1,1010
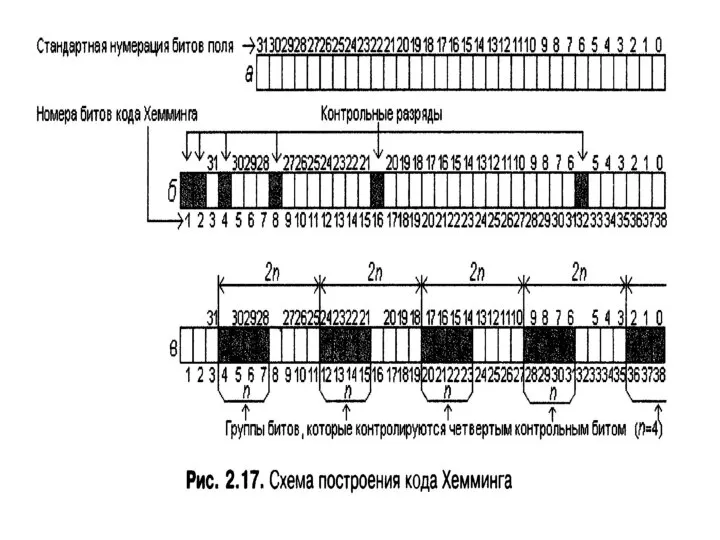
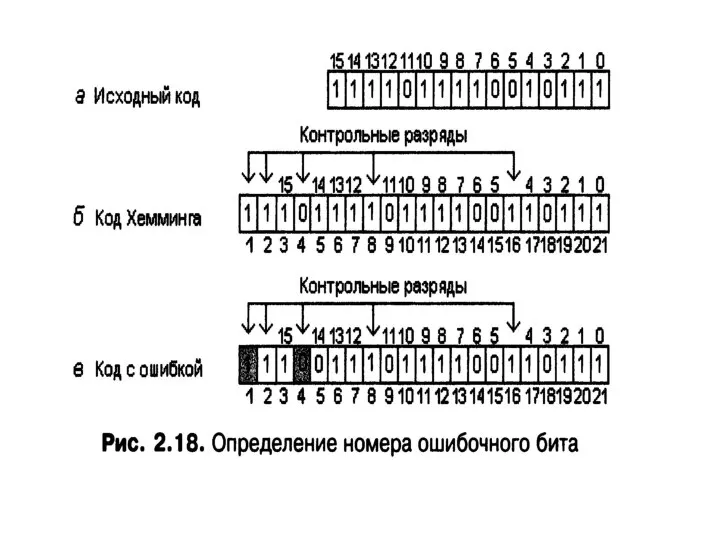
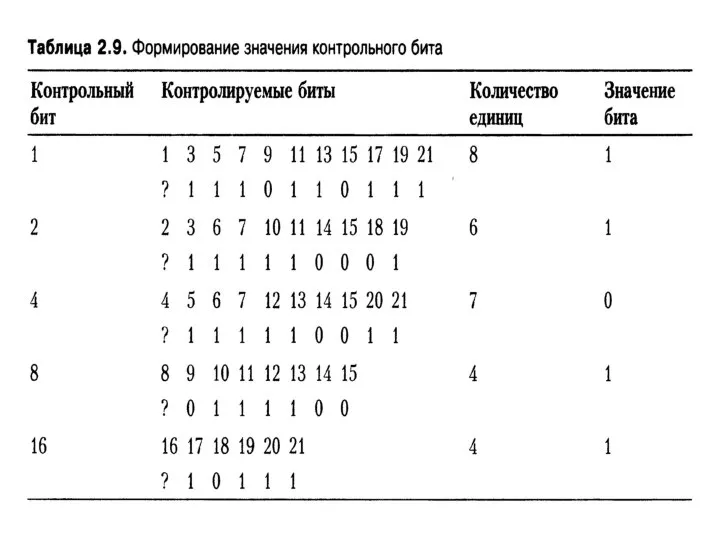
- 65. Алгоритм построения кодов по Хеммингу
- 72. Скачать презентацию
































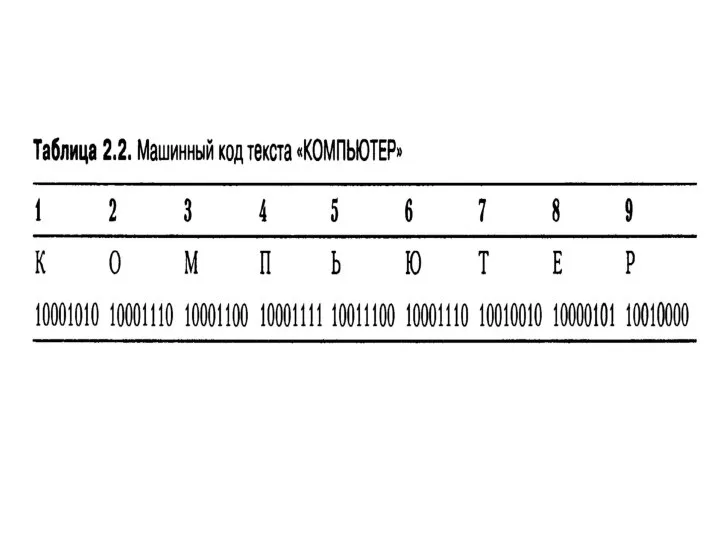
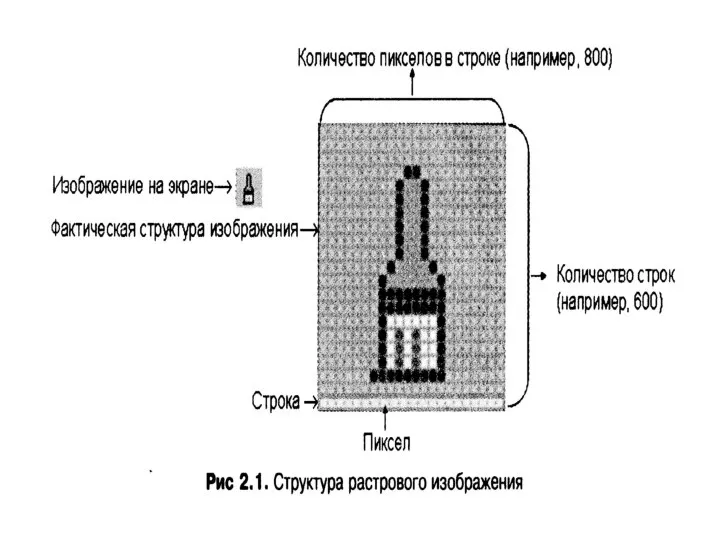
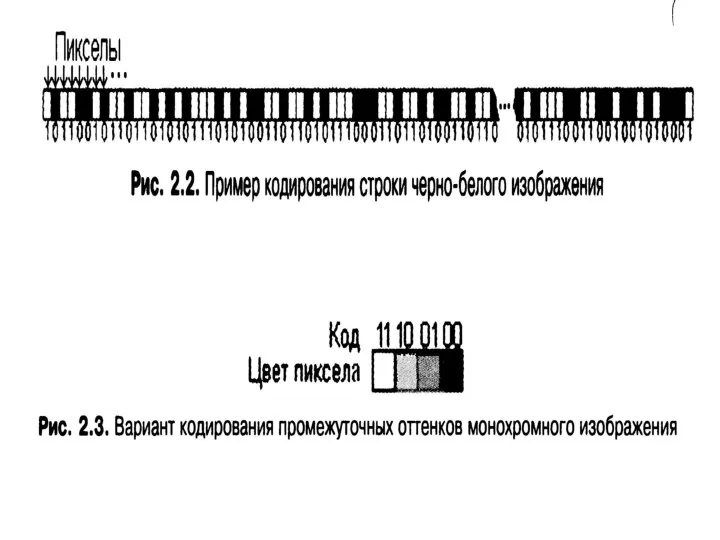
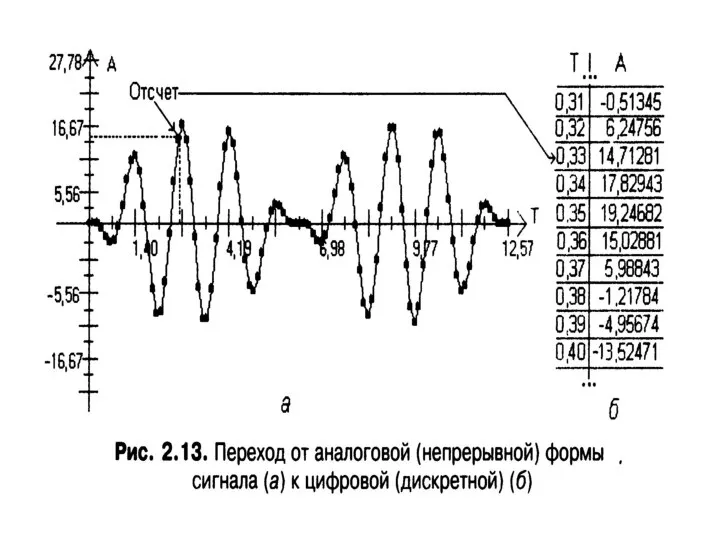



 Архитектура ЭВМ
Архитектура ЭВМ Подпись в МФЦ
Подпись в МФЦ Компьютерная арифметика
Компьютерная арифметика Мир медиа. Опечатки и ошибки в российской прессе
Мир медиа. Опечатки и ошибки в российской прессе Преимущества перехода на ЮЗЭДО
Преимущества перехода на ЮЗЭДО Введение в программу CorelDRAW
Введение в программу CorelDRAW Сomputer game in the bartender simulator
Сomputer game in the bartender simulator Понятие о системах поддержки принятия решений и экспертных системах
Понятие о системах поддержки принятия решений и экспертных системах Устройство персонального компьютера
Устройство персонального компьютера Алгоритм успеха
Алгоритм успеха Создание видеофильмов системными средствами Windows 7
Создание видеофильмов системными средствами Windows 7 Гигатест
Гигатест Файлы и файловая система. Что такое файл?
Файлы и файловая система. Что такое файл? Логическое следствие. Анализ рассуждений. Лекция 4
Логическое следствие. Анализ рассуждений. Лекция 4 Наследование классов. Пример лабораторной 2
Наследование классов. Пример лабораторной 2 Презентация на тему Адресация в Интернет
Презентация на тему Адресация в Интернет  Носители информации
Носители информации Բջջային հեռախոս. Համացանցից օգտվելու հնարավորություն
Բջջային հեռախոս. Համացանցից օգտվելու հնարավորություն Информация и информационные процессы. Таблица степеней двойки
Информация и информационные процессы. Таблица степеней двойки Краснодарский государственный историко-археологический музей-заповедник им. Е.Д. Фелицына
Краснодарский государственный историко-археологический музей-заповедник им. Е.Д. Фелицына Проектирование,информационное моделирование (bim) и визуализация гражданских и промышленных зданий
Проектирование,информационное моделирование (bim) и визуализация гражданских и промышленных зданий Chronos v4.0
Chronos v4.0 Мультисайтовость
Мультисайтовость Настройка политики безопасности для корпоративной сети на основе GPO в ООО Виктория
Настройка политики безопасности для корпоративной сети на основе GPO в ООО Виктория На чём держатся сети?
На чём держатся сети? Информационные технологии в туризме
Информационные технологии в туризме УТП, техники копирайтинга
УТП, техники копирайтинга Графы. Часть 5
Графы. Часть 5