Арифметичні і логічні основи цифрових і електронних обчислювальних машин

Арифметичні основи
Системи числення
Непозиційна система числення (кожен символ зберігає своє значення незалежно від його місця (позиції) в числі)
Позиційна система числення (кожен символ має своє значення в залежності від місця (позиції) в числі)
2596,23 = 2·1000+5·100+9·10+6·1+2·0,1+3·0,01 = =2·103+5·102+9·101+6·100+2·10-1+3·10-2

Загальна алгебраїчна форма числа в позиційній системі числення
аі - кількість одиниць і-того розряду числа, аі<Р
P - основа системи числення
Pi - називають вагою розряду
(15)10 (1011)2 (735)8 (1EA9F)16
1510 10112 7358 1EA9F16
15D 1011B 735Q 1EA9FH

Двійкова система числення

Вісімкова система числення

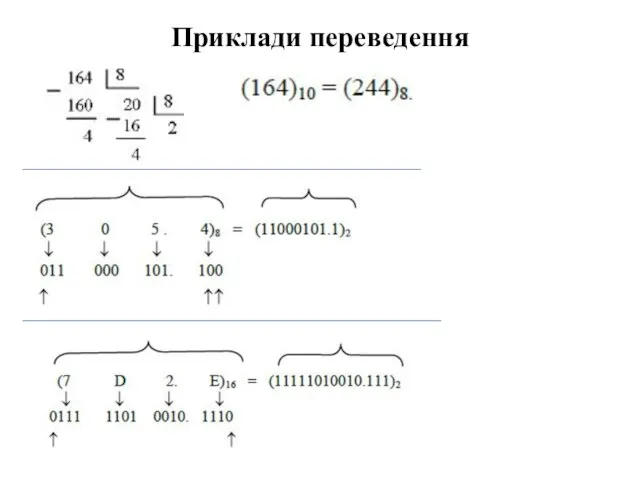
Шістнадцяткова система числення

Переведення числа з двійкової системи числення і навпаки

Приклади переведення

Форми представлення чисел
Представлення чисел з фіксованою комою (крапкою)

Представлення чисел з плаваючою комою (крапкою)

Нормалізовані числа

Розрядна сітка машини з плаваючою комою

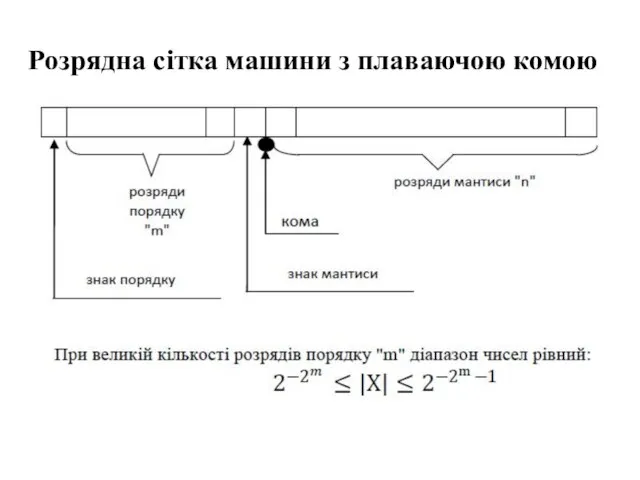
Кодування чисел
Прямий код
Прямий код додатних і від'ємних чисел відрізняється від зображення самих чисел тільки значенням знакового розряду. Для додатних чисел в цьому розряді записують "0", а для від'ємних "1".
Х = + 0,11001101 Х = - 0,11001101
[X]пр. = 0,11001101 [Х]пр. = 1,11001101
Обернений код
Обернений код додатного числа співпадає по зображенню з самим числом. Щоб утворити обернений код від'ємного числа необхідно – в знаковому розряді записати "1", а числові розряди проінвертувати, тобто нулі замінити одиницями, а одиниці – нулями.
Х = + 0,11001101 Х = - 0,11001101
[X]об. = 0,11001101 [Х]об. = 1,00110010

Доповняльний код
Цей код найчастіше використовується в обчислювальній техніці.
Доповняльний код додатного числа співпадає по зображенню з самим числом.
Щоб утворити доповняльний код від'ємного числа необхідно - в знаковому розряді записати "1", числові розряди про інвертувати і до молодшого розряду додати 1.
Х = + 0,11001101 Х = - 0,11001101
[X]доп. = 0,11001101 [X]доп = 1,00110011
Цей код називається доповняльним тому, що сума розрядів від'ємного числа і числових розрядів [ ]доп. дорівнюють 1.
,11001101
+,00110011
1,00000000

Операції додавання та віднімання двійкових чисел з фіксованою комою

Операції додавання та віднімання двійкових чисел з плаваючою комою
Дано: Х1 = 10100·(+0,10011010); Х2 = 10100·(+0,10111011)
Порядки рівні тому виконують додавання мантис.
[МX1]доп. = 0,10011010
[МX2]доп. = 0,10111011
[МX1+МХ2]доп. = 1,01010101
Одиниця в знаковому розряді виникла тому, що сума мантис стала більшою 1.
Нормалізуємо мантису вправо, зсуваючи її на один розряд вправо: [МX1+МХ2]доп. = 0,10101010 |1
пам'ятаючи, що порядок результату необхідно збільшити на 1.
Заокруглюють результат, якщо при зсуві вправо за межі розрядної сітки вийшла 1. Її додають до сусіднього старшого розряду
[МX1+МХ2]доп. = 0,10101011
Тому, що сума мантис додатна, можна записати:
МX1+МХ2. = + 0,10101011
Результат рівний
Х + Y = 10101 ·(+0,10101011)

Логічні основи
Булева алгебра. Алгебра логіки оперує висловами.
Висловом називається будь-яке твердження, по відношенню до якого можна сказати істинне воно, чи хибне. Вважають, якщо вислів істинний – він рівний "1", якщо хибний – він рівний "0".
Вислови можуть бути простими і складними. Прості – це такі вислови, які вміщають одну закінчену думку. Складні вислови складаються з двох або більше простих висловів.
Як прості так і складні вислови можуть приймати тільки два значення "0" або "1", тобто можуть бути істинними чи хибними. Прості вислови називають вхідними перемінними, а складні – логічними функціями вхідних перемінних.

Таблиця істинності

Логічні зв’язки і логічні елементи
Більш компактною формою запису логічних функцій є алгебраїчний вираз, до складу якого входять вхідні перемінні Х, що зв'язані між собою логічними зв'язками (логічними операціями). Електронними схемами, що реалізують логічні операції називають логічними елементами. Основних логічних операцій є три:
І, НЕ, АБО
Вони складають так-звану функціонально повну систему, тобто з їх допомогою можна описати будь-яку логічну функцію.

Логічна операція "НЕ" (інверсія, заперечення)

Логічна операція "АБО" (диз'юнкція, логічне додавання)

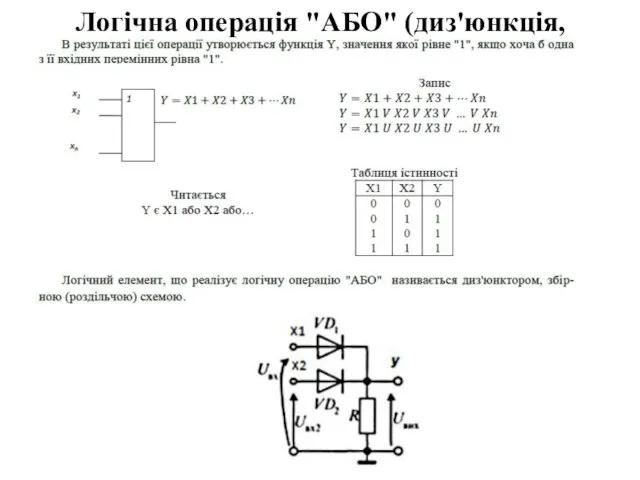
Логічна операція "І" (кон'юкція, логічне множення)

Логічна операція нерівнозначності

Логічна операція рівнозначності (еквівалентність)

Логічна операція "АБО-НЕ" (стрілка Пірса)

Логічна операція "І-НЕ" (штрих Шеффера)

Аксіоми алгебри логіки