Бинарные деревья

Рекурсивная функция просмотра списка
void prosmotr_2(struct element *tek)
{
if( tek != NULL )
{
printf("%d", tek->d);
prosmotr_2(tek->link);
}
}

Рекурсивная функция построения списка
void vvod_2(struct elemeny **t)
{
int i;
scanf("%d", &i); if (i != 0)
{
*t=(struct element *)malloc(sizeof(struct element));
(*t)->d = i;
vvod_2(&((*t)->link));
}
else
*t=NULL;
}

Функция main()
int main()
{
struct element *nach;
vvod_2(&nach);
prosmotr_2(nach);
. . .
}

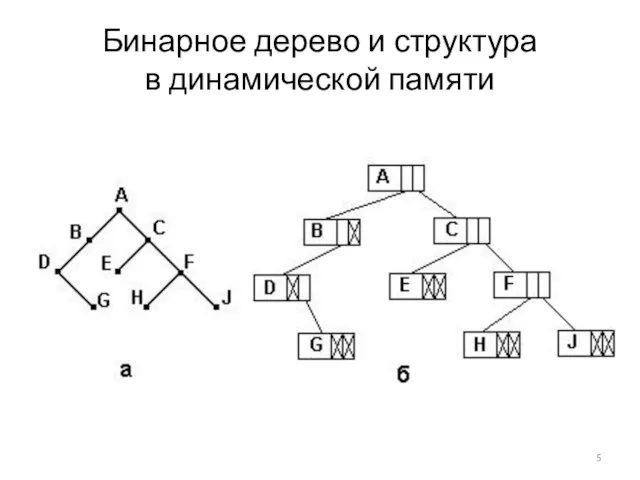
Бинарное дерево и структура
в динамической памяти

Способы обхода деревьев
Сверху (прямой порядок прохождения дерева);
Слева направо (обратный порядок);
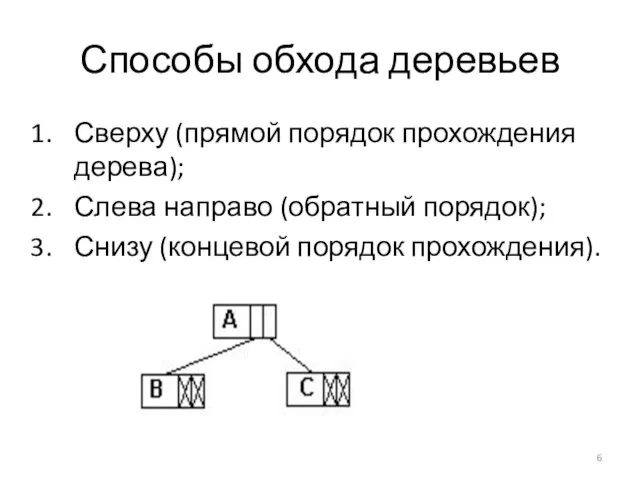
Снизу (концевой порядок прохождения).

Алгоритм 1. Прямой порядок.
Попасть в корень.
Пройти левое поддерево.
Пройти правое поддерево
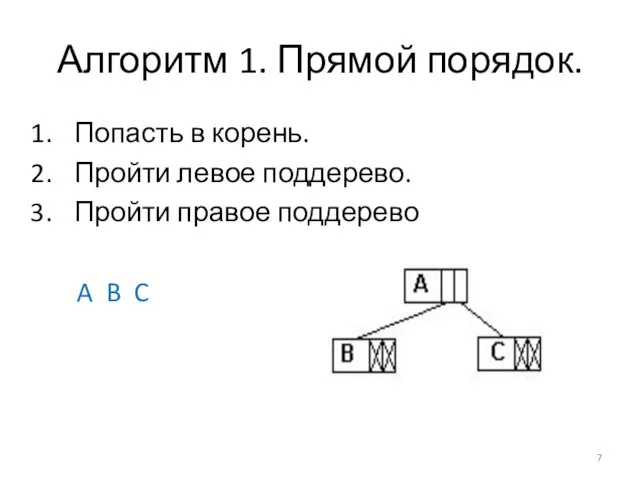
A B C

Алгоритм 2. Обратный порядок.
Пройти левое поддерево.
Попасть в корень.
Пройти правое поддерево.
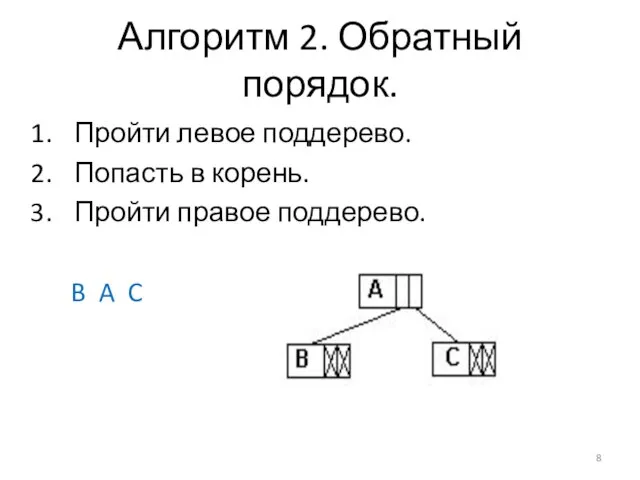
B A C

Алгоритм 3. Концевой порядок.
Пройти левое поддерево.
Пройти правое поддерево.
Попасть в корень.
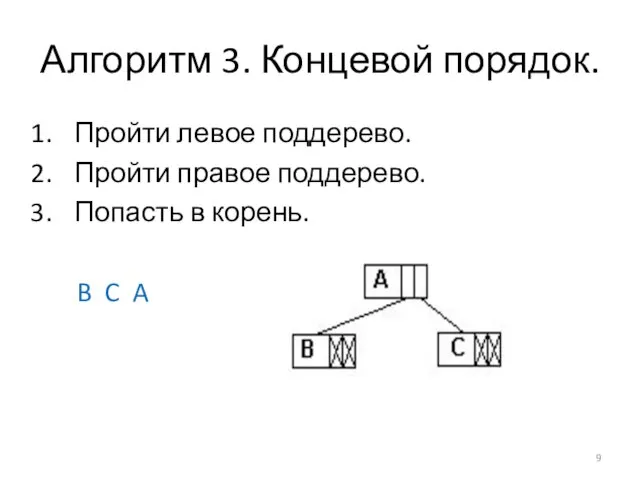
B C A

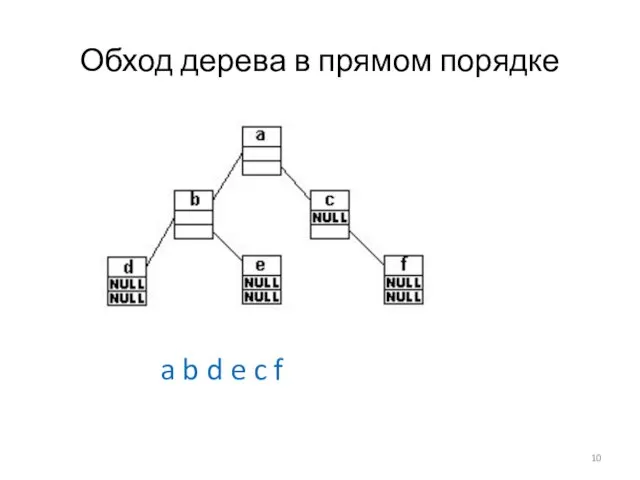
Обход дерева в прямом порядке
a b d e c f

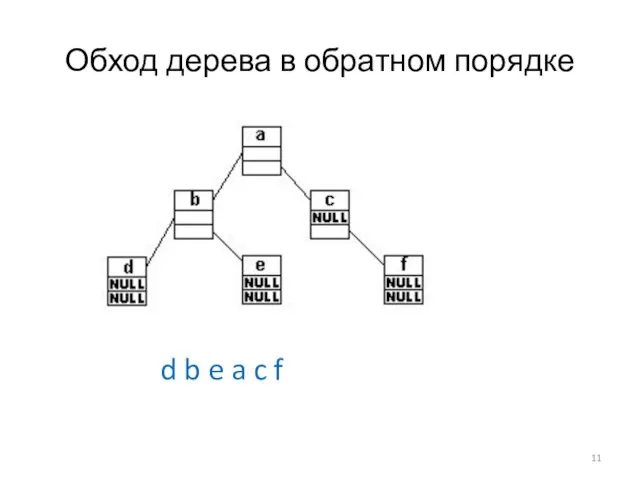
Обход дерева в обратном порядке
d b e a c f

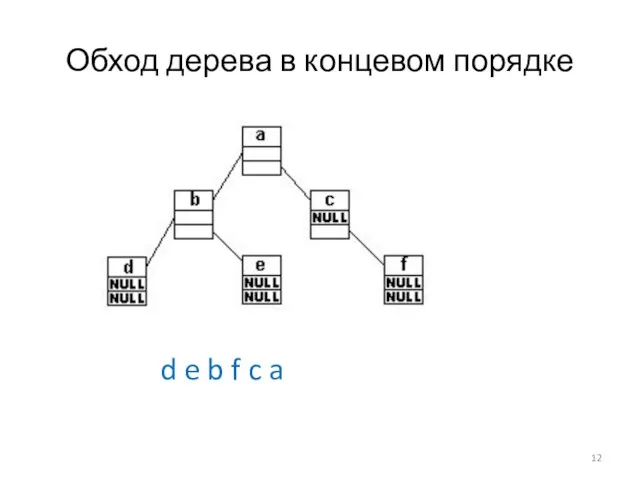
Обход дерева в концевом порядке
d e b f c a

Описание типа
struct node
{
char info;
struct node *llink;
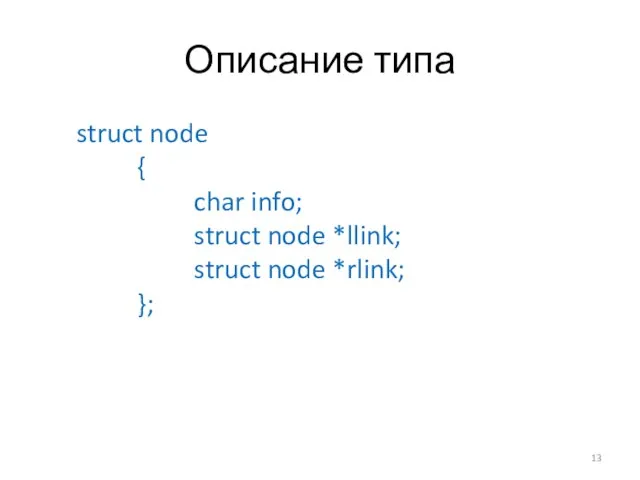
struct node *rlink;
};

Функция main()
int main()
{
struct node *root;
vtree(&root);
btree(root);
btree2();
return 0;
}

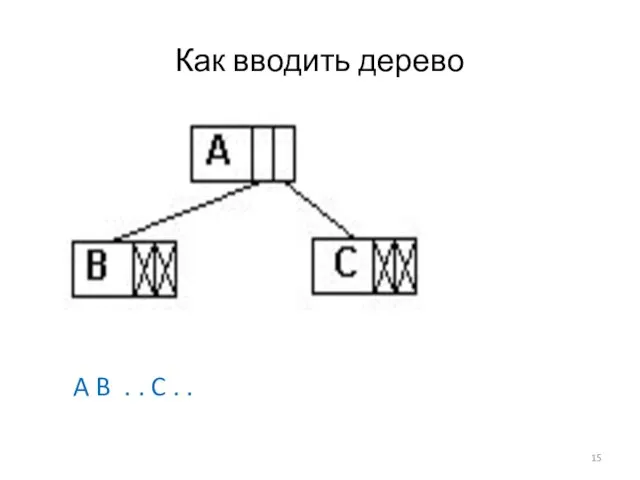
Как вводить дерево
A B . . C . .

Рекурсивная функция построения
бинарного дерев
Параметр функции – указатель на указатель на корень дерева
Вершины дерева – символьные данные

void vtree(struct node **t)
{
char c;
scanf("%c", &c);
if (c != ’.’)
{
*t=(struct node *)malloc(sizeof(struct node ));
(*t)->info=c;
vtree(&((*t)->llink));
vtree(&((*t)->rlink));
}
else
*t=NULL;
}

Как вводить дерево
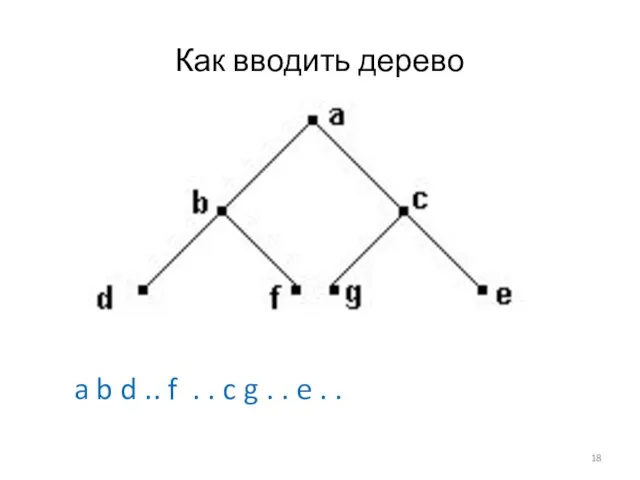
a b d .. f . . c g . . e . .

Как вводить дерево
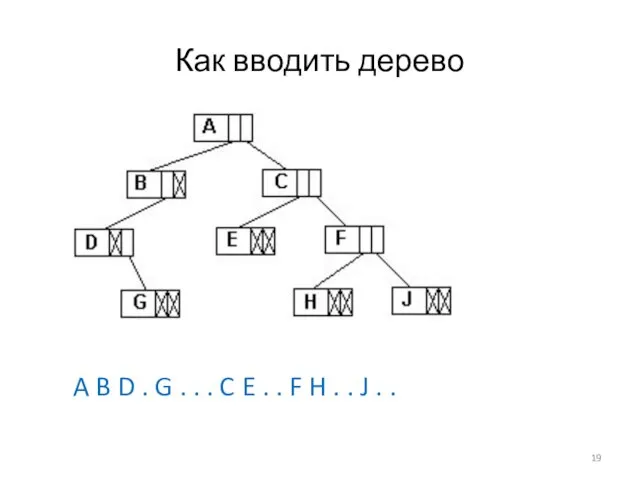
A B D . G . . . C E . . F H . . J . .

Функция рекурсивного обхода дерева
void btree(struct node *t)
{
if (t != NULL)
{ btree(t->llink); // обойти левое поддерево
printf("%c ", t->info); // попасть в корень
btree(t->rlink); // обойти правое поддерево
}
}

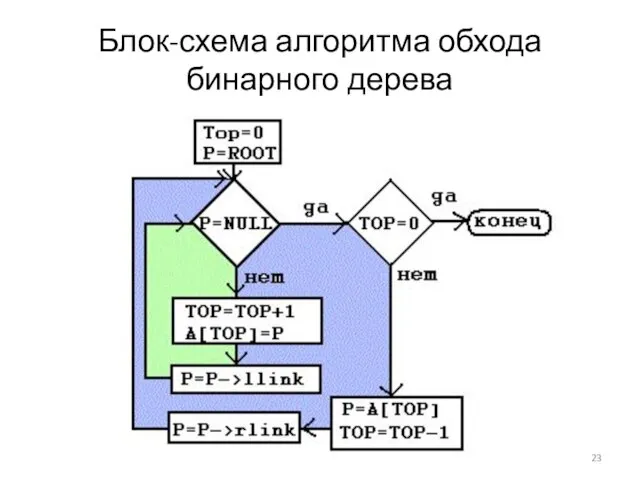
Алгоритм стекового обхода дерева
ROOT – указатель на бинарное дерево;
А – стек, в который заносятся адреса еще не пройденных вершин;
TOP – вершина стека;
P – рабочая переменная-указатель.

Алгоритм стекового обхода дерева
Начальная установка:
TOP = 0; P = ROOT;
Если P = NULL, то перейти на 4 (конец ветви).
Вершину заносим в стек:
TOP = TOP+1; A[TOP] = P;
шаг по левой ветви: P = P->llink;
перейти на 2 (идем по левой ветви).
Если TOP = 0, то КОНЕЦ.
Достаем вершину из стека:
P = A[TOP]; TOP = TOP-1;
Шаг по правой связи: P = P->rlink;
перейти на 2.

Блок-схема алгоритма обхода
бинарного дерева