Содержание
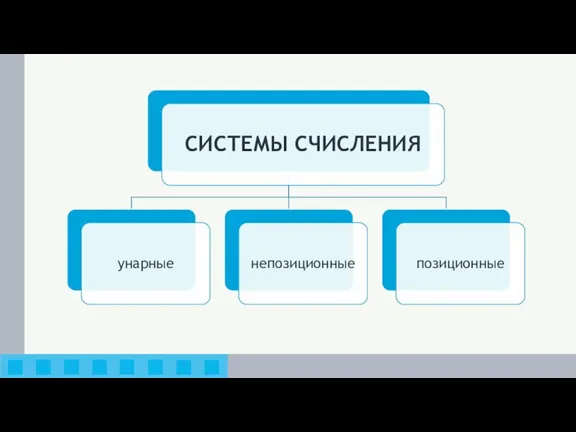
- 2. КЛЮЧЕВЫЕ СЛОВА система счисления цифра алфавит непозиционная система счисления позиционная система счисления основание системы счисления развёрнутая
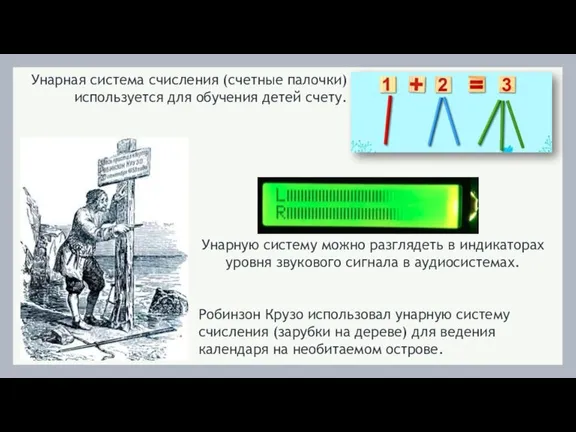
- 5. Простейшая и самая древняя система - унарная система счисления. В ней для записи любых чисел используется
- 6. Простейшая и самая древняя система - унарная система счисления. В ней для записи любых чисел используется
- 7. Простейшая и самая древняя система - унарная система счисления. В ней для записи любых чисел используется
- 8. Робинзон Крузо использовал унарную систему счисления (зарубки на дереве) для ведения календаря на необитаемом острове. Унарная
- 9. ДРЕВНЕЕГИПЕТСКАЯ СИСТЕМА СЧИСЛЕНИЯ 1235
- 10. НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Система счисления называется непозиционной, если количественный эквивалент цифры не зависит от её положения
- 11. РИМСКАЯ СИСТЕМА СЧИСЛЕНИЯ
- 12. ЗАПИСЬ ЧИСЕЛ В РИМСКОЙ СИСТЕМЕ СЧИСЛЕНИЯ В наши дни любую из римских цифр предлагается использовать в
- 13. Алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила: каждый меньший знак,
- 14. СЛАВЯНСКАЯ КИРИЛЛИЧЕСКАЯ СИСТЕМА СЧИСЛЕНИЯ 55 288 1 498
- 15. ПОЗИЦИОННАЯ СИСТЕМА СЧИСЛЕНИЯ Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения в
- 16. ПРИМЕР
- 17. УЗЛОВЫЕ И АЛГОРИТМИЧЕСКИЕ ЧИСЛА Узловые числа обозначаются цифрами. × 100 + × 10 + = Алгоритмические
- 18. Начало десятичной системе счисления было положено в древнем Египте и Вавилоне. В основном её формирование было
- 19. Существует множество позиционных систем счисления. Основанием позиционной системы счисления может служить любое натуральное число q >
- 20. СИСТЕМА СЧИСЛЕНИЯ С ОСНОВАНИЕМ 5 Основание: 5 Алфавит: 0, 1, 2, 3, 4 Базис: 1, 5,
- 21. СИСТЕМА СЧИСЛЕНИЯ С ОСНОВАНИЕМ q Основание: q Алфавит: 0, 1, …, q – 1 Базис: 1,
- 22. Развернутая форма записи целого положительного числа: Aq = an-1⋅q n-1 + an-2⋅q n-2 + … +
- 23. 5432 = 5000 + 400 + 30 + 2 5432 = 5×1000 + 4×100 + 3×10
- 24. Степени основания определяют количественный эквивалент цифры в записи числа. Развернутая форма записи числа – запись числа
- 25. Развернутая форма записи числа – запись числа в виде суммы разрядных слагаемых. 54328 = 5×83 +
- 26. КАК ЗАПИСАТЬ ЧИСЛО В РАЗВЕРНУТОЙ ФОРМЕ 1) Выписать число в свернутой форме 2) Над цифрами числа
- 27. КАК ПЕРЕВЕСТИ ЧИСЛО В ДЕСЯТИЧНУЮ СИСТЕМУ СЧИСЛЕНИЯ Чтобы перевести число из позиционной системы счисления с основанием
- 28. КАК СРАВНИТЬ ЧИСЛА, ЗАПИСАННЫЕ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ 1) Записать каждое из чисел в развернутой форме.
- 29. ВОПРОСЫ И ЗАДАНИЯ Чем различаются унарные, позиционные и непозиционные системы счисления?
- 30. ВОПРОСЫ И ЗАДАНИЯ На постаменте памятника Петру I в Санкт-Петербурге римскими цифрами записан год открытия памятника:
- 31. ВОПРОСЫ И ЗАДАНИЯ Как вы считаете, почему позиционные системы счисления с основаниями 5, 10, 12 и
- 32. ВОПРОСЫ И ЗАДАНИЯ Как от свёрнутой формы записи десятичного числа перейти к его развёрнутой форме?
- 33. ВОПРОСЫ И ЗАДАНИЯ Запишите в развёрнутом виде числа: а) 143,51110 б) 1435118 в) 14351116
- 34. ВОПРОСЫ И ЗАДАНИЯ Запишите числа в свернутой форме: а) 5×103 +0×102 +3×101 +1×100 = б) 1×104
- 35. ВОПРОСЫ И ЗАДАНИЯ Запишите десятичные числа в развернутой форме: а) 2021 б) 435 в) 3008
- 36. ВОПРОСЫ И ЗАДАНИЯ Вычислите десятичные эквиваленты следующих чисел: а) 1728; б) 21916; в) 1010102; г) 2436.
- 37. ВОПРОСЫ И ЗАДАНИЯ Укажите, какое из чисел 1100112, 1114, 358 и 1616 является: а) наибольшим; б)
- 38. ВОПРОСЫ И ЗАДАНИЯ Верны ли следующие равенства? а) 334 = 217; б) 337 = 214.
- 39. ВОПРОСЫ И ЗАДАНИЯ Найдите основание х системы счисления, если: а) 14x = 910; б) 2002x =
- 40. ВОПРОСЫ И ЗАДАНИЯ Какое двузначное в десятичной системе счисления число окажется «круглым» (с двумя нулями в
- 42. Скачать презентацию





































 6-12-1-grafiki-i-diagrammy
6-12-1-grafiki-i-diagrammy Медиатекст: дефиниция, основные свойства, типология
Медиатекст: дефиниция, основные свойства, типология Отчет
Отчет SkyDNS-облачный контент-фильтр
SkyDNS-облачный контент-фильтр Texity. По строй город прямо в Telegram
Texity. По строй город прямо в Telegram Отдел программирования и автоматизации
Отдел программирования и автоматизации Upravlenie_i_kibernetika
Upravlenie_i_kibernetika Дискретное (цифровое) представление информации
Дискретное (цифровое) представление информации Алгоритмы и структуры данных. Стеки и очереди
Алгоритмы и структуры данных. Стеки и очереди Тормоза 1С – откуда и как с ними бороться
Тормоза 1С – откуда и как с ними бороться Алгебра высказываний
Алгебра высказываний Локальная сеть
Локальная сеть Алгоритмы и структуры данных на Python. Хеш-функции, хеши, хештаблицы
Алгоритмы и структуры данных на Python. Хеш-функции, хеши, хештаблицы Средства связи и массовой информации. Интернет
Средства связи и массовой информации. Интернет Медиа-карта региона: культура
Медиа-карта региона: культура Отслеживание ошибок. Методы предотвращения ошибок во время разработки
Отслеживание ошибок. Методы предотвращения ошибок во время разработки Финальный отчёт
Финальный отчёт Лекция 3 - презентация
Лекция 3 - презентация Поразрядная LSD - сортировка. Лекция 5
Поразрядная LSD - сортировка. Лекция 5 Работай, хватит в фейсбуке сидеть! или как построить личный бренд
Работай, хватит в фейсбуке сидеть! или как построить личный бренд Предметно-ориентированное проектирование автоматизированных систем управления
Предметно-ориентированное проектирование автоматизированных систем управления prez_0
prez_0 Операционная система
Операционная система Prezentatsia_Microsoft_PowerPoint (1)
Prezentatsia_Microsoft_PowerPoint (1) Исследование физических моделей
Исследование физических моделей Творческое объединение робототехника. Программирование и робототехника (занятия 18, 19)
Творческое объединение робототехника. Программирование и робототехника (занятия 18, 19) Язык программирования Паскаль
Язык программирования Паскаль YarMama.Информационный портал
YarMama.Информационный портал