Динамические структуры данных. Лекция 10 (продолжение)

Стеки
Вопрос 3

Особенности стека
Стек – это частный случай однонаправленного списка, добавление элементов в который и выборка из которого выполняются с одного конца, называемого вершиной стека.
Другие операции со стеком не определены.
При выборке элемент исключается из стека.
Стек реализует принцип обслуживания LIFO (last in – first out, последним пришел – первым ушел).

Пример программы
Задание:
Программа должна формировать стек из пяти целых чисел (1,2, 3, 4, 5) и выводить его на экран.
Замечания:
Функция помещения в стек по традиции называется push, а выборки – pop.
Указатель для работы со стеком (top) всегда ссылается на его вершину.

Текст программы
#include "stdafx.h"
#include "conio.h"
#include
using namespace std;
//Структура, описывающая элемент стека
struct Node{
int d;
Node *p;
};

Текст программы
//Список функций программы
Node * first(int d);
void push(Node **top, int d);
int pop(Node **top);

Текст программы
int _tmain(int argc, _TCHAR* argv[])
{
Node *top = first(1); //Формирование первого //элемента стека
for (int i = 2; i<6; i++) //Заполнение стека
push(&top, i);
while (top) //Вывод
// содержимого стека на экран
cout << pop(&top) << ' ';
getch();
return 0;
}

Текст программы
//Функция начального формирования стека
Node *first(int d)
{
Node *pv = new Node;
pv->d = d;
pv->p = 0;
return pv;
}

Текст программы
//Функция занесения нового элемента в стек
void push(Node **top, int d)
{
Node *pv = new Node;
pv->d = d;
pv->p = *top;
*top = pv;
}

Текст программы
//Функция выборки элемента из стека
int pop(Node **top)
{
int temp = (*top)->d;
Node *pv = *top;
*top = (*top)->p;
delete pv;
return temp;
}

Результат
Результат работы программы
5 4 3 2 1

Очереди
Вопрос 4

Особенности
Очередь – это частный случай однонаправленного списка, добавление элементов в который выполняется в один конец, а выборка – из другого конца.
Другие операции с очередью не определены.
При выборке элемент исключается из очереди.
Очередь реализует принцип обслуживания FIFO (first in – first out, первым пришел – первым ушел)

Пример программы
Задание:
Программа должна формировать очередь из пяти целых чисел (1,2, 3, 4, 5) и выводить его на экран.
Замечание:
Функция помещения в конец очереди называется add, а выборки – del. Указатель на начало очереди называется pbeg, указатель на конец – pend.

Текст программы
#include "stdafx.h"
#include "conio.h"
#include
using namespace std;
//Структура, описывающая элемент очереди
struct Node{
int d;
Node *p;
};

Текст программы
//Список функций программы
Node *first(int d);
void add(Node **pend, int d);
int del(Node **pbeg);

Текст программы
int _tmain(int argc, _TCHAR* argv[])
{
Node *pbeg = first(1); // Формирование первого // элемента очереди
Node *pend = pbeg;
for (int i = 2; i<6; i++) // Заполнение очереди
add(&pend, i);
while (pbeg) // Выборка элементов из // очереди
cout << del(&pbeg) << ' ';
getch();
return 0;
}

Текст программы
//Функция формирования первого элемента очереди
Node *first(int d)
{
Node *pv = new Node;
pv->d = d;
pv->p = 0;
return pv;
}

Текст программы
//Функция добавления элемента в конец очереди
void add(Node **pend, int d)
{
Node *pv = new Node;
pv->d = d;
pv->p = 0;
(*pend)->p = pv;
*pend = pv;
}

Текст программы
//Функция выборки элементов из очереди
int del(Node **pbeg)
{
int temp = (*pbeg)->d;
Node *pv = *pbeg;
*pbeg = (*pbeg)->p;
delete pv;
return temp;
}

Результат
Результат работы программы
1 2 3 4 5

Бинарные деревья
Вопрос 5

Особенности
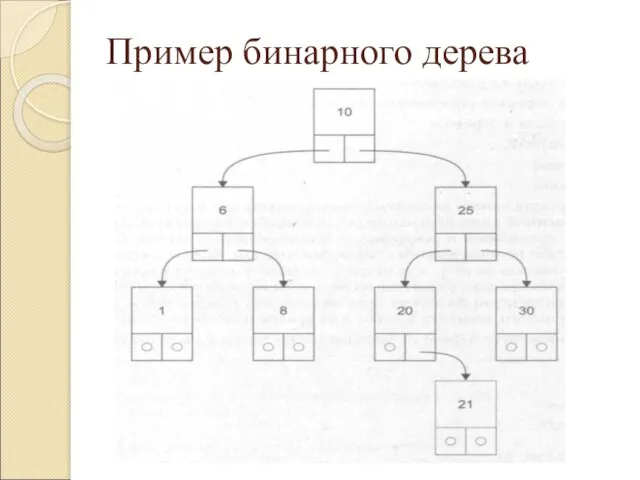
Бинарное дерево – это динамическая структура данных, состоящая из узлов, каждый из которых содержит, кроме данных, не более двух ссылок на различные узлы бинарного дерева.
На каждый узел имеется ровно одна ссылка.
Начальный узел называется корнем дерева.

Пример бинарного дерева

Дерево поиска
Если дерево организовано таким образом, что для каждого узла все ключи его левого поддерева меньше ключа этого узла, а все ключи его правого поддерева – больше, оно называется деревом поиска.
Одинаковые ключи не допускаются.
В дереве поиска можно найти элемент по ключу, двигаясь от корня и переходя на левое или правое поддерево в зависимости от значения ключа в каждом узле.

Рекурсивная функция обхода узлов дерева
function way_around ( дерево )
{
way_around ( левое поддерево )
посещение корня
way_around ( правое поддерево )
}

Операции с бинарными деревьями
– включение узла в дерево;
– поиск по дереву;
– обход дерева;
– удаление узла.

Пример программы
Задание:
Программа должна формировать дерево из массива целых чисел и выводит его на экран.
Замечание:
Текущий указатель для поиска по дереву обозначен pv, указатель на предка pv обозначен prev, переменная pnew используется для выделения памяти под включаемый в дерево узел.

Текст программы
#include "stdafx.h"
#include "conio.h"
#include
using namespace std;
//Структура описывающая узел дерева
struct Node{
int d;
Node *left;
Node *right;
};

Текст программы
//Список функций программы
Node *first(int d);
Node *search_insert(Node *root, int d);
void print_tree(Node *root, int level);

Текст программы
int _tmain(int argc, _TCHAR* argv[])
{
// Массив для формирования дерева
int b[] = {10, 25, 20, 6, 21, 8, 1, 30};
Node *root = first(b[0]); // Создание корня дерева
for (int i = 1; i<8; i++)
search_insert(root, b[i]); // Размещение элементов
// на дереве
print_tree(root, 0); // Вывод элементов
//бинарного дерева
// на экран
getch();
return 0;
}

Текст программы
//Функция формирования первого элемента дерева
Node *first(int d){
Node *pv = new Node;
pv->d = d;
pv->left = 0;
pv->right = 0;
return pv;
}

Текст программы
//Функция поиска с включением узла в дерево
Node *search_insert(Node *root, int d)
{
Node *pv = root, *prev;
bool found = false;
while (pv && !found)
{
prev = pv;
if (d == pv->d)
found = true;
else
if (d < pv->d)
pv = pv->left;
else
pv = pv->right;
}

Текст программы
if (found)
return pv;
Node *pnew = new Node;
pnew->d = d;
pnew->left = 0;
pnew->right = 0;
if (d < prev->d)
// Присоединение к левому поддереву предка
prev->left = pnew;
else
// Присоединение к правому поддереву предка
prev->right = pnew;
return pnew;
}

Текст программы
//Функция обхода дерева
void print_tree(Node *p, int level)
{
if (p)
{
print_tree(p->left, level+1); // вывод левого // поддерева
for (int i = 0; i
cout << " ";
cout << p->d << "\n"; // вывод корня // поддерева
print_tree(p->right, level + 1); // вывод правого // поддерева
}
}