Содержание
- 2. Тема 1. Указатели © К.Ю. Поляков, 2008 Динамические структуры данных (язык Си)
- 3. Статические данные переменная (массив) имеет имя, по которому к ней можно обращаться размер заранее известен (задается
- 4. Динамические данные размер заранее неизвестен, определяется во время работы программы память выделяется во время работы программы
- 5. Указатели Указатель – это переменная, в которую можно записывать адрес другой переменной (или блока памяти). Объявление:
- 6. Обращение к данным Как работать с данными через указатель? Как работать с массивами? int m =
- 7. Что надо знать об указателях указатель – это переменная, в которой можно хранить адрес другой переменной;
- 8. Тема 2. Динамические массивы © К.Ю. Поляков, 2008 Динамические структуры данных (язык Си)
- 9. Где нужны динамические массивы? Задача. Ввести размер массива, затем – элементы массива. Отсортировать массив и вывести
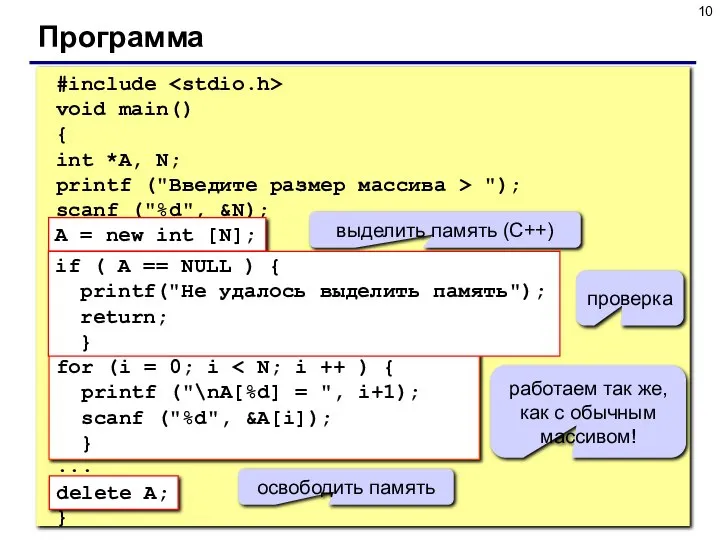
- 10. Программа #include void main() { int *A, N; printf ("Введите размер массива > "); scanf ("%d",
- 11. Динамические массивы для выделения памяти в языке Си используются функции malloc и calloc; в языке C++
- 12. Ошибки при работе с памятью Запись в «чужую» область памяти: память не была выделена, а массив
- 13. Динамические матрицы Задача. Ввести размеры матрицы и выделить для нее место в памяти во время работы
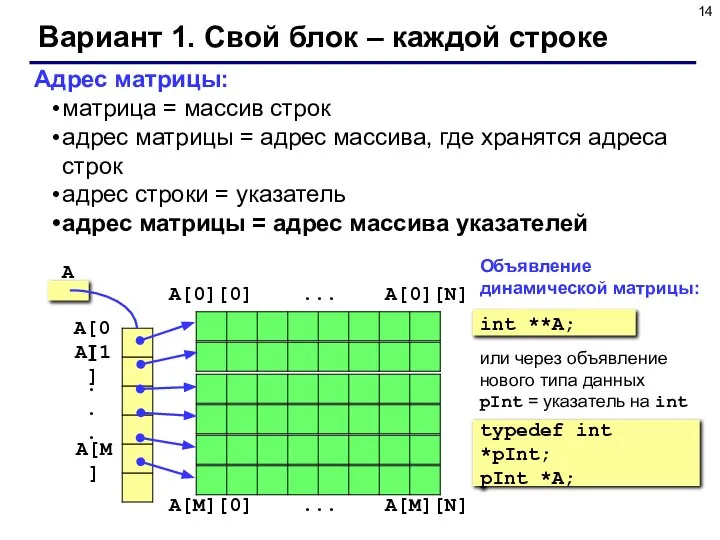
- 14. Вариант 1. Свой блок – каждой строке Адрес матрицы: матрица = массив строк адрес матрицы =
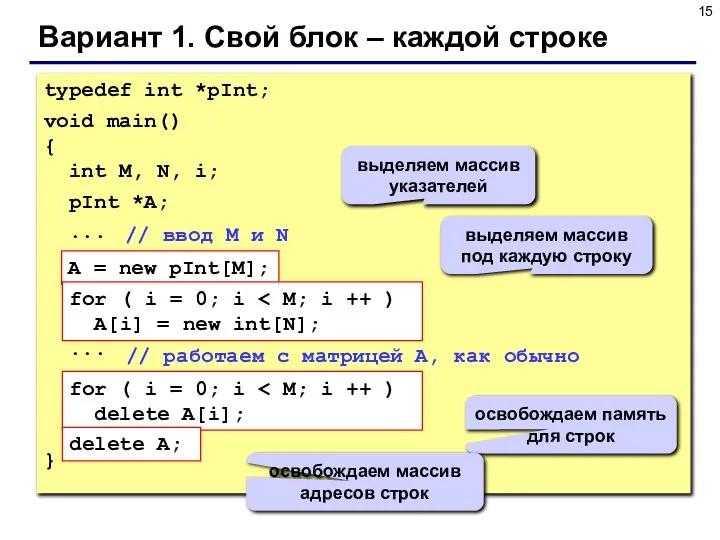
- 15. Вариант 1. Свой блок – каждой строке typedef int *pInt; void main() { int M, N,
- 16. Вариант 2. Один блок на матрицу A Выделение памяти: A[0] ... A[M] A[0][0] … A[1][0] …
- 17. Тема 3. Структуры © К.Ю. Поляков, 2008 Динамические структуры данных (язык Си)
- 18. Структуры Структура – это тип данных, который может включать в себя несколько полей – элементов разных
- 19. Как работать со структурами? Объявление: Book b; // здесь выделяется память! Book b1 = { "А.С.
- 20. Копирование структур По элементам: Book b1, b2; ... // здесь вводим b1 strcpy ( b2.author, b1.author
- 21. Массивы структур Объявление: Book B[10]; Обращение к полям: for ( i = 0; i B[i].year =
- 22. Пример программы Задача: в файле books.dat записаны данные о книгах в виде массива структур типа Book
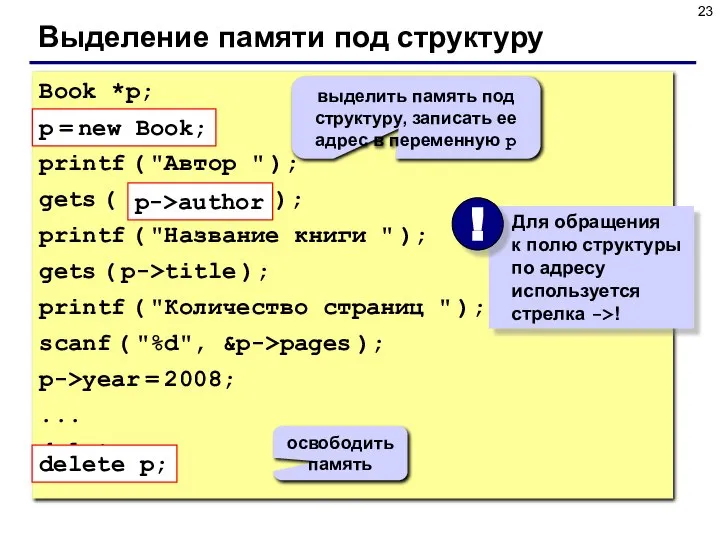
- 23. Выделение памяти под структуру Book *p; p = new Book; printf ( "Автор " ); gets
- 24. Динамические массивы структур Book *B; int n; printf ( "Сколько у вас книг? " ); scanf
- 25. Сортировка массива структур Ключ (ключевое поле) – это поле, по которому сортируются структуры. Проблема: как избежать
- 26. Реализация в программе const N = 10; Book B[N]; Book *p[N], *temp; int i, j; ...
- 27. Тема 4. Списки © К.Ю. Поляков, 2008 Динамические структуры данных (язык Си)
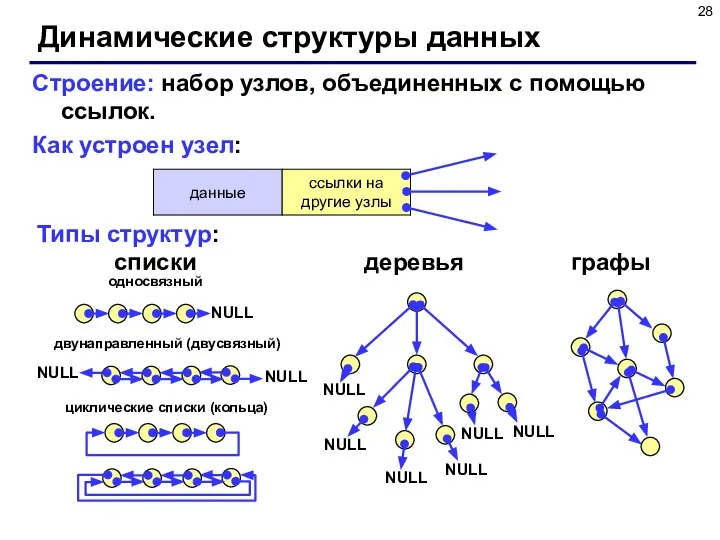
- 28. Динамические структуры данных Строение: набор узлов, объединенных с помощью ссылок. Как устроен узел: Типы структур: списки
- 29. Когда нужны списки? Задача (алфавитно-частотный словарь). В файле записан текст. Нужно записать в другой файл в
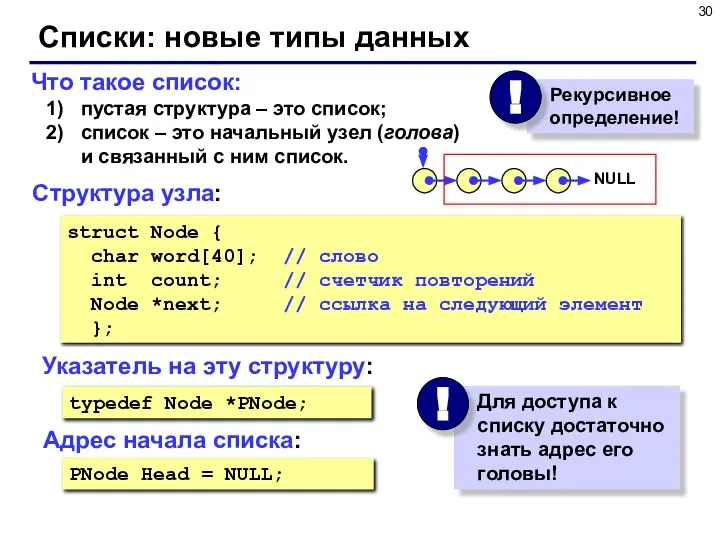
- 30. Что такое список: пустая структура – это список; список – это начальный узел (голова) и связанный
- 31. Что нужно уметь делать со списком? Создать новый узел. Добавить узел: в начало списка; в конец
- 32. Создание узла PNode CreateNode ( char NewWord[] ) { PNode NewNode = new Node; strcpy(NewNode->word, NewWord);
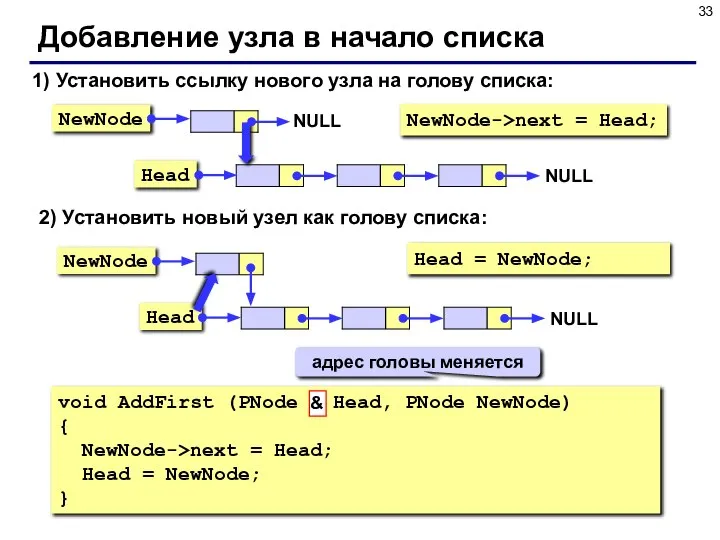
- 33. Добавление узла в начало списка 1) Установить ссылку нового узла на голову списка: NewNode->next = Head;
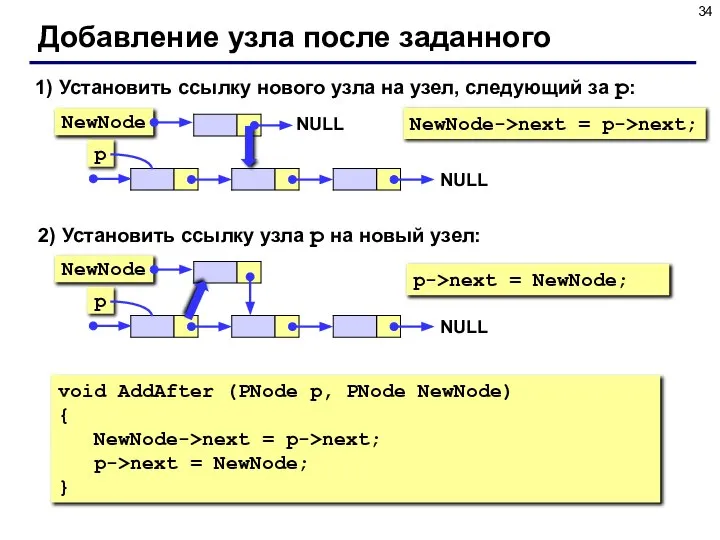
- 34. Добавление узла после заданного 1) Установить ссылку нового узла на узел, следующий за p: NewNode->next =
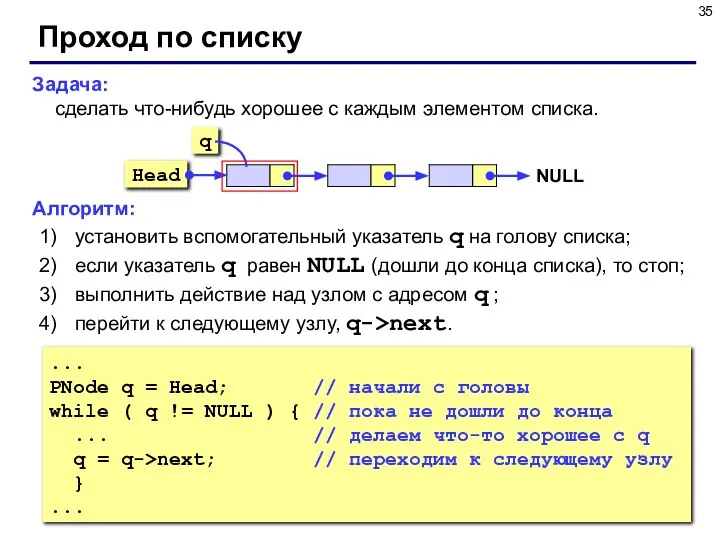
- 35. Задача: сделать что-нибудь хорошее с каждым элементом списка. Алгоритм: установить вспомогательный указатель q на голову списка;
- 36. Добавление узла в конец списка Задача: добавить новый узел в конец списка. Алгоритм: найти последний узел
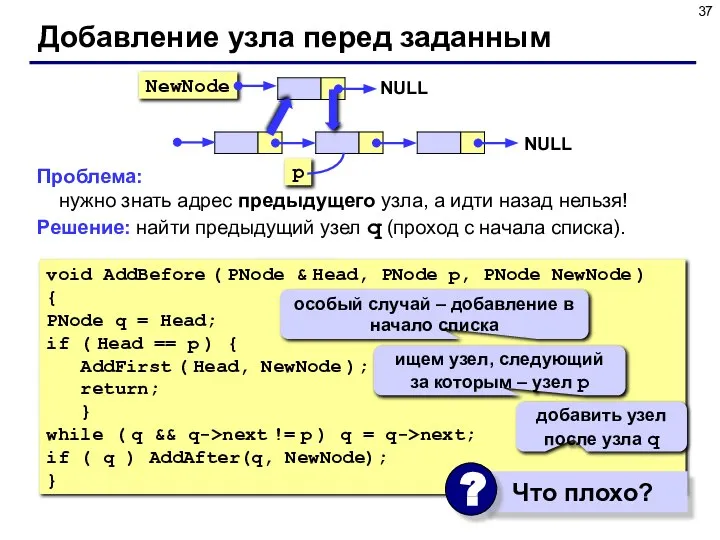
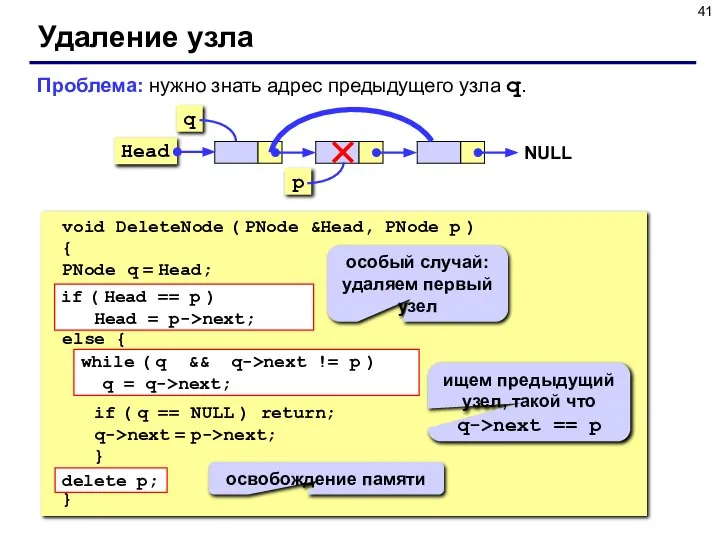
- 37. Проблема: нужно знать адрес предыдущего узла, а идти назад нельзя! Решение: найти предыдущий узел q (проход
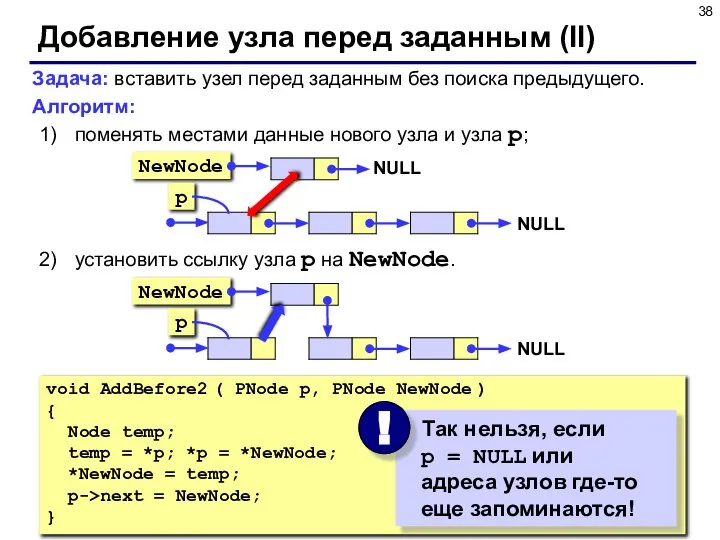
- 38. Добавление узла перед заданным (II) Задача: вставить узел перед заданным без поиска предыдущего. Алгоритм: поменять местами
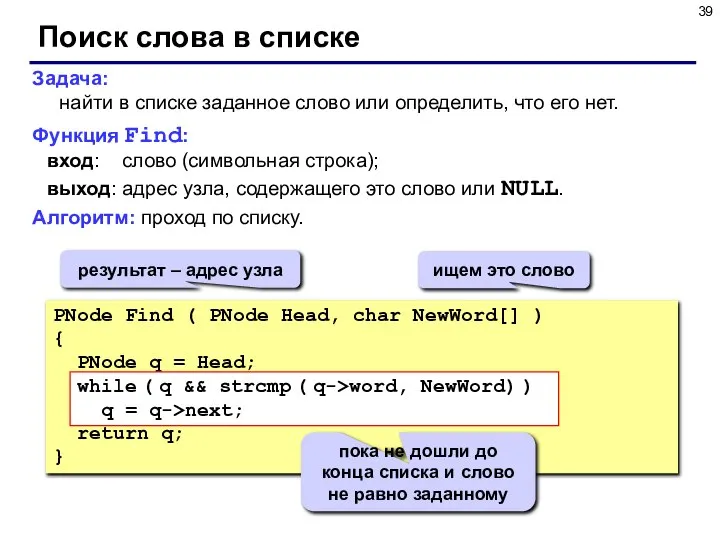
- 39. Поиск слова в списке Задача: найти в списке заданное слово или определить, что его нет. Функция
- 40. Куда вставить новое слово? Задача: найти узел, перед которым нужно вставить, заданное слово, так чтобы в
- 41. Удаление узла void DeleteNode ( PNode &Head, PNode p ) { PNode q = Head; if
- 42. Алфавитно-частотный словарь Алгоритм: открыть файл на чтение; прочитать слово: если файл закончился (n!=1), то перейти к
- 43. Двусвязные списки Структура узла: struct Node { char word[40]; // слово int count; // счетчик повторений
- 44. Задания «4»: «Собрать» из этих функций программу для построения алфавитно-частотного словаря. В конце файла вывести общее
- 45. Тема 5. Стеки, очереди, деки © К.Ю. Поляков, 2008 Динамические структуры данных (язык Си)
- 46. Стек Стек – это линейная структура данных, в которой добавление и удаление элементов возможно только с
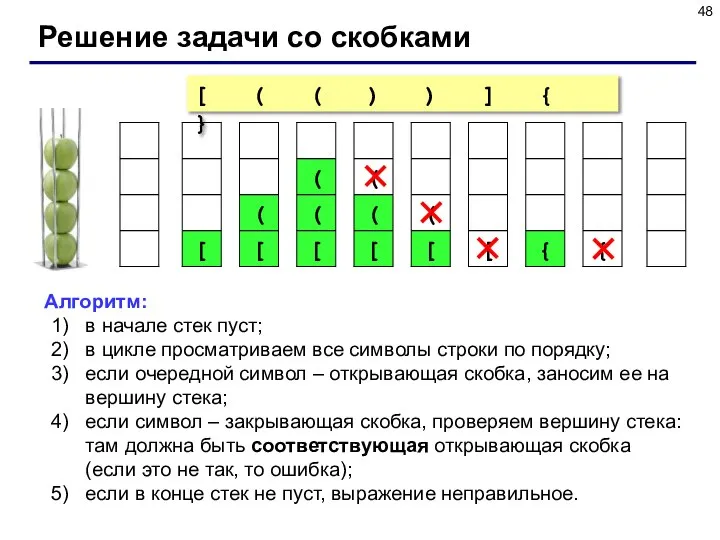
- 47. Пример задачи Задача: вводится символьная строка, в которой записано выражение со скобками трех типов: [], {}
- 48. Решение задачи со скобками Алгоритм: в начале стек пуст; в цикле просматриваем все символы строки по
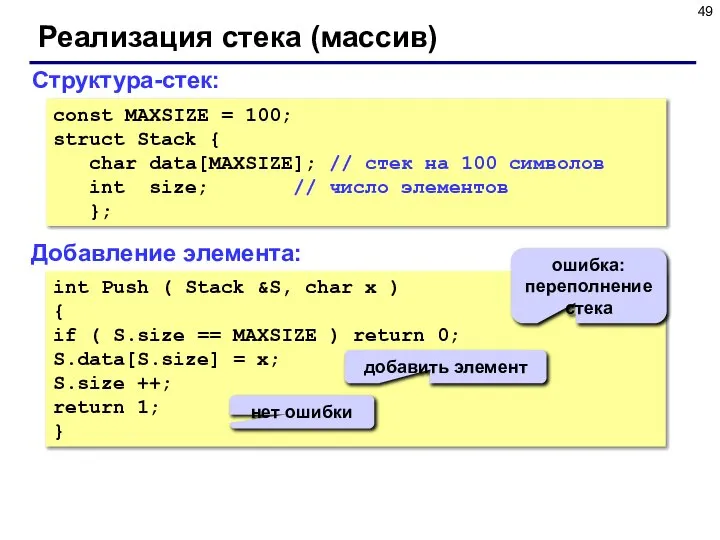
- 49. Реализация стека (массив) Структура-стек: const MAXSIZE = 100; struct Stack { char data[MAXSIZE]; // стек на
- 50. Реализация стека (массив) char Pop ( Stack &S ) { if ( S.size == 0 )
- 51. Программа void main() { char br1[3] = { '(', '[', '{' }; char br2[3] = {
- 52. Обработка строки (основной цикл) for ( i = 0; i { for ( k = 0;
- 53. Реализация стека (список) Добавление элемента: Структура узла: struct Node { char data; Node *next; }; typedef
- 54. Реализация стека (список) Снятие элемента с вершины: char Pop (PNode &Head) { char x; PNode q
- 55. Вычисление арифметических выражений a b + c d + 1 - / Как вычислять автоматически: Инфиксная
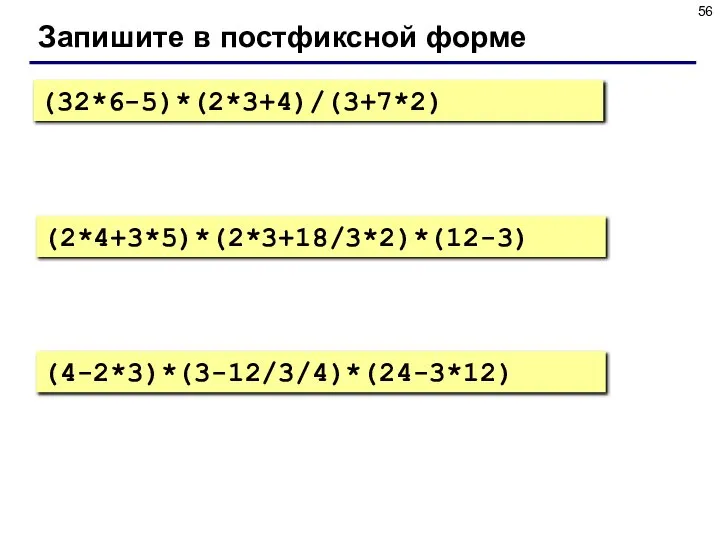
- 56. Запишите в постфиксной форме (32*6-5)*(2*3+4)/(3+7*2) (2*4+3*5)*(2*3+18/3*2)*(12-3) (4-2*3)*(3-12/3/4)*(24-3*12)
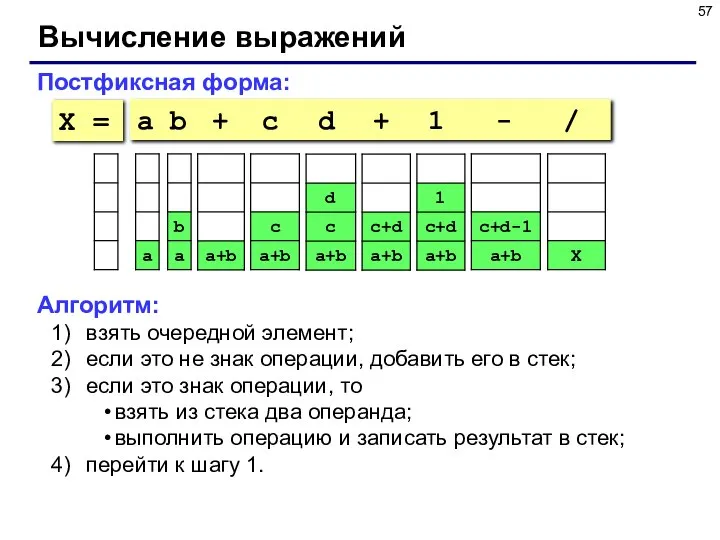
- 57. Вычисление выражений Постфиксная форма: a b + c d + 1 - / Алгоритм: взять очередной
- 58. Системный стек (Windows – 1 Мб) Используется для размещения локальных переменных; хранения адресов возврата (по которым
- 59. Очередь Очередь – это линейная структура данных, в которой добавление элементов возможно только с одного конца
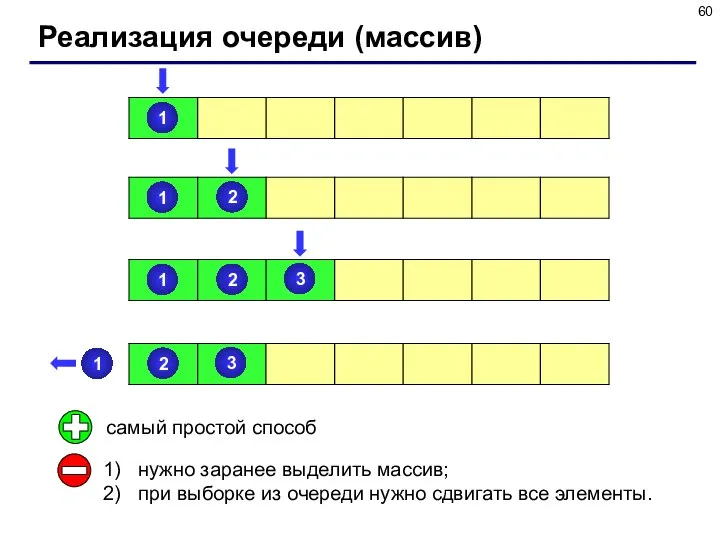
- 60. Реализация очереди (массив) самый простой способ нужно заранее выделить массив; при выборке из очереди нужно сдвигать
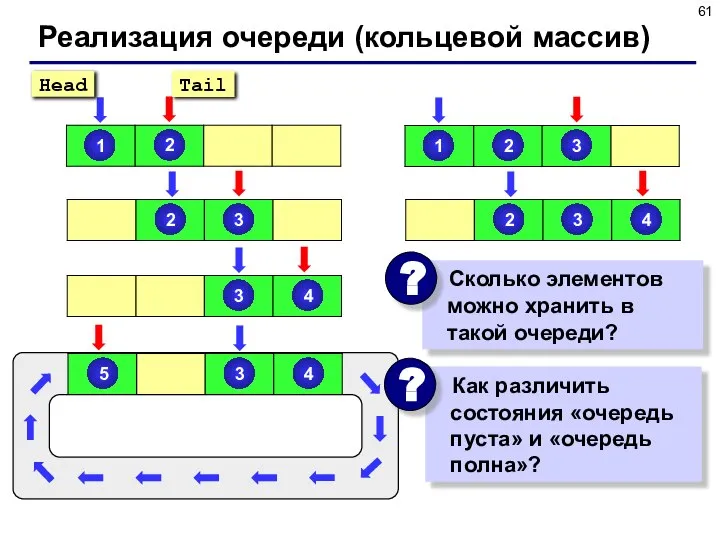
- 61. Реализация очереди (кольцевой массив)
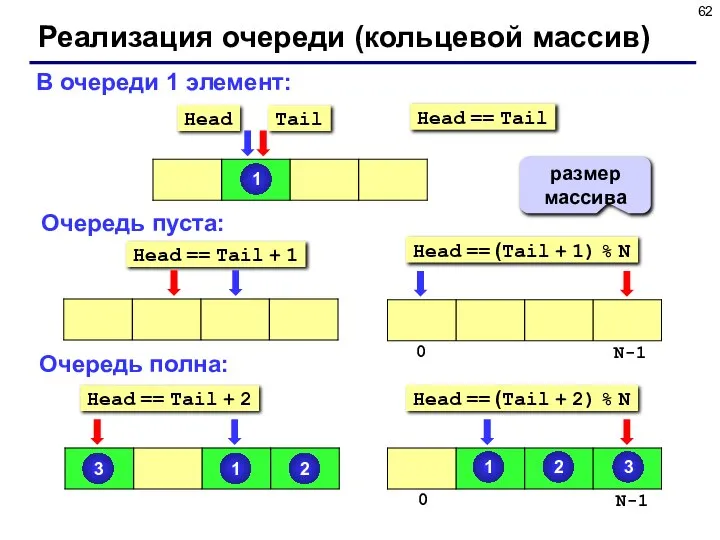
- 62. Реализация очереди (кольцевой массив) В очереди 1 элемент: Очередь пуста: Очередь полна: Head == Tail +
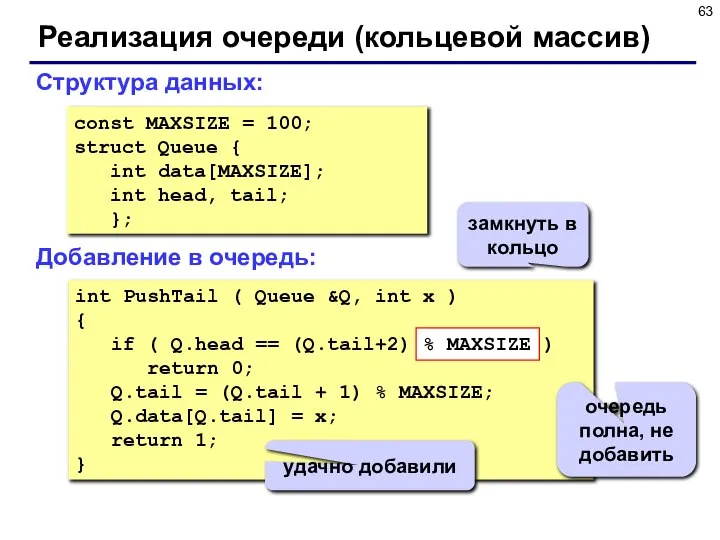
- 63. Реализация очереди (кольцевой массив) const MAXSIZE = 100; struct Queue { int data[MAXSIZE]; int head, tail;
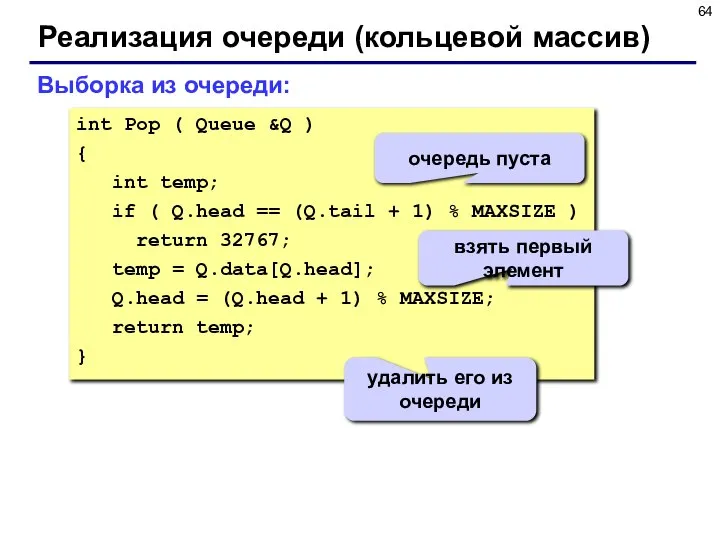
- 64. Реализация очереди (кольцевой массив) Выборка из очереди: int Pop ( Queue &Q ) { int temp;
- 65. Реализация очереди (списки) struct Node { int data; Node *next; }; typedef Node *PNode; struct Queue
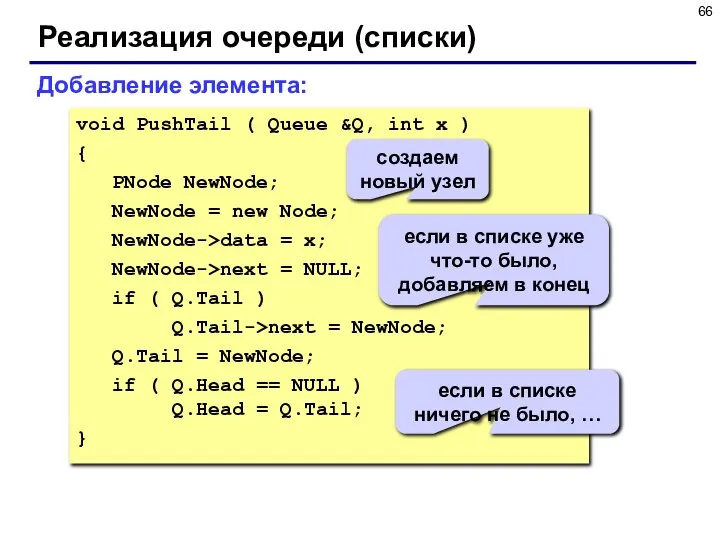
- 66. Реализация очереди (списки) void PushTail ( Queue &Q, int x ) { PNode NewNode; NewNode =
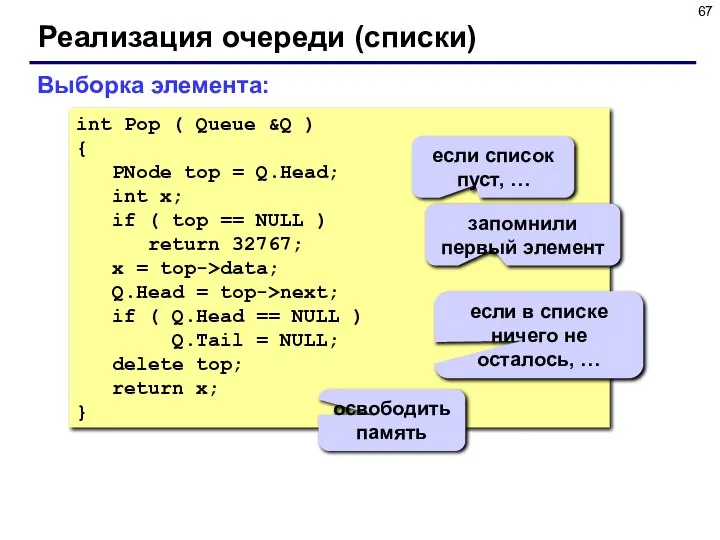
- 67. Реализация очереди (списки) int Pop ( Queue &Q ) { PNode top = Q.Head; int x;
- 68. Дек Дек (deque = double ended queue, очередь с двумя концами) – это линейная структура данных,
- 69. Задания «4»: В файле input.dat находится список чисел (или слов). Переписать его в файл output.dat в
- 70. Тема 6. Деревья © К.Ю. Поляков, 2008 Динамические структуры данных (язык Си)
- 71. Деревья
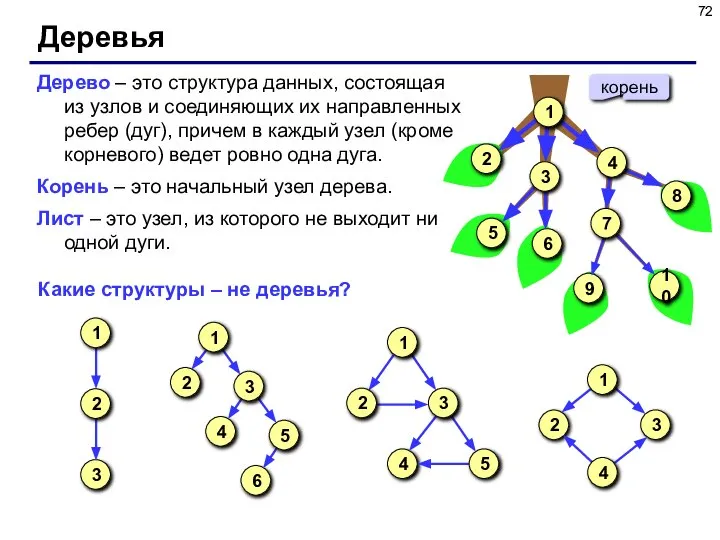
- 72. Деревья Дерево – это структура данных, состоящая из узлов и соединяющих их направленных ребер (дуг), причем
- 73. Деревья Предок узла x – это узел, из которого существует путь по стрелкам в узел x.
- 74. Дерево – рекурсивная структура данных Рекурсивное определение: Пустая структура – это дерево. Дерево – это корень
- 75. Двоичные деревья Структура узла: struct Node { int data; // полезные данные Node *left, *right; //
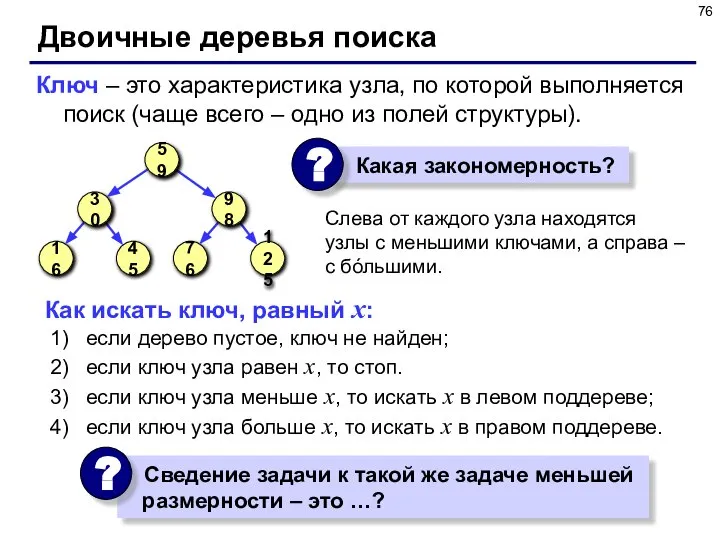
- 76. Двоичные деревья поиска Слева от каждого узла находятся узлы с меньшими ключами, а справа – с
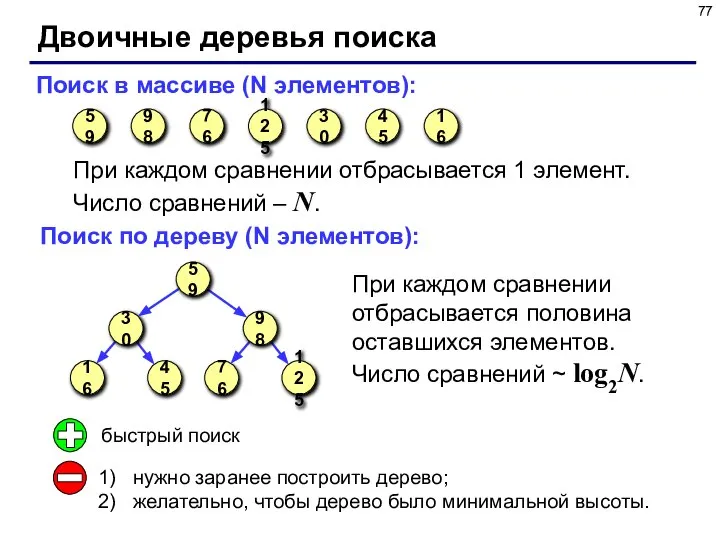
- 77. Двоичные деревья поиска Поиск в массиве (N элементов): При каждом сравнении отбрасывается 1 элемент. Число сравнений
- 78. Реализация алгоритма поиска //--------------------------------------- // Функция Search – поиск по дереву // Вход: Tree - адрес
- 79. Как построить дерево поиска? //--------------------------------------------- // Функция AddToTree – добавить элемент к дереву // Вход: Tree
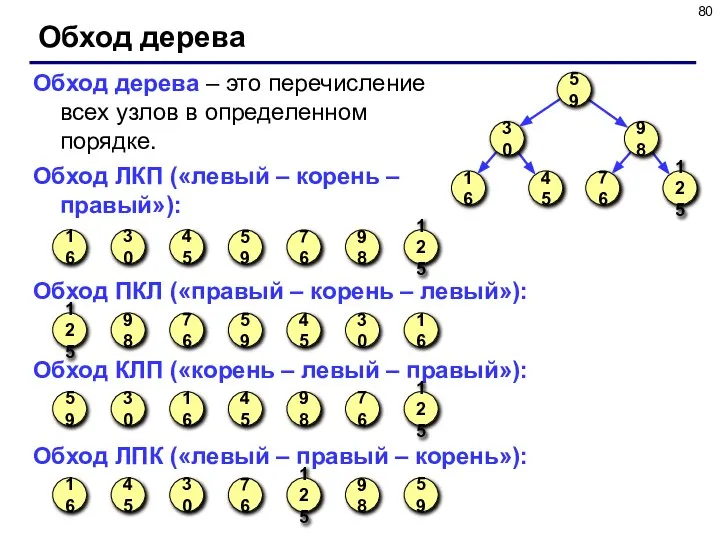
- 80. Обход дерева Обход дерева – это перечисление всех узлов в определенном порядке. Обход ЛКП («левый –
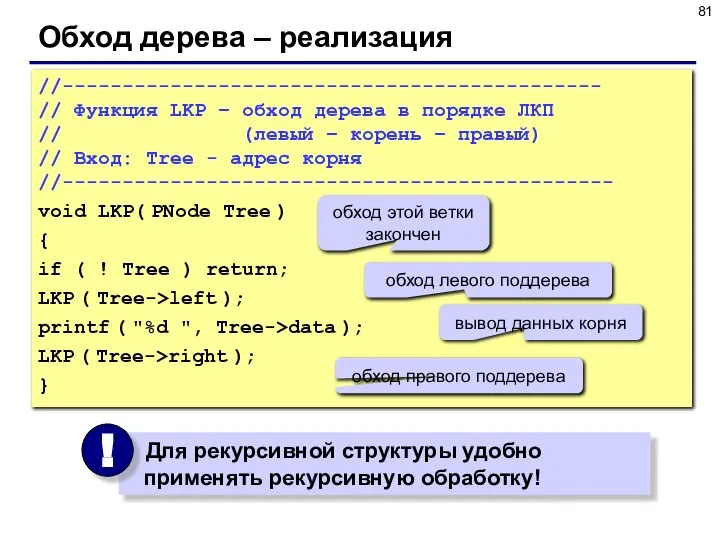
- 81. Обход дерева – реализация //--------------------------------------------- // Функция LKP – обход дерева в порядке ЛКП // (левый
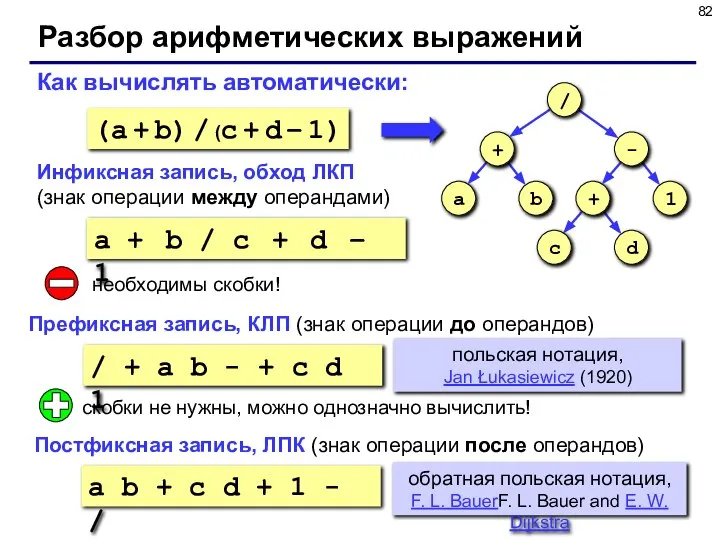
- 82. Разбор арифметических выражений a b + c d + 1 - / Как вычислять автоматически: Инфиксная
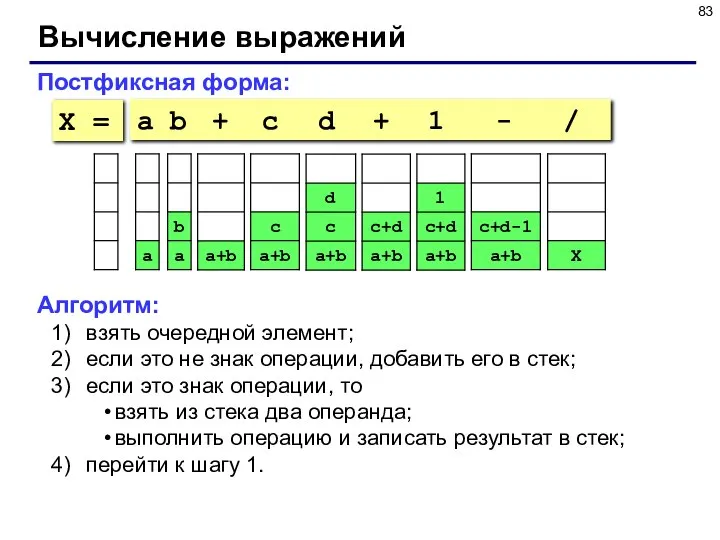
- 83. Вычисление выражений Постфиксная форма: a b + c d + 1 - / Алгоритм: взять очередной
- 84. Вычисление выражений Задача: в символьной строке записано правильное арифметическое выражение, которое может содержать только однозначные числа
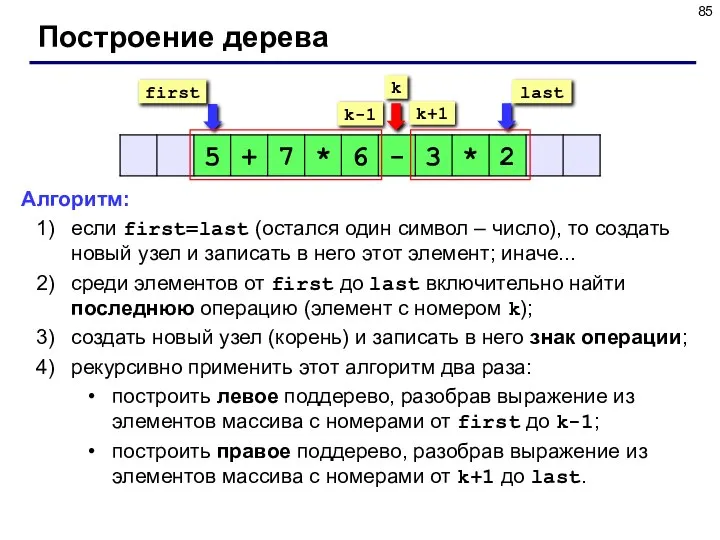
- 85. Построение дерева Алгоритм: если first=last (остался один символ – число), то создать новый узел и записать
- 86. Как найти последнюю операцию? Порядок выполнения операций умножение и деление; сложение и вычитание. Приоритет (старшинство) –
- 87. Приоритет операции //-------------------------------------------- // Функция Priority – приоритет операции // Вход: символ операции // Выход: приоритет
- 88. Номер последней операции //-------------------------------------------- // Функция LastOperation – номер последней операции // Вход: строка, номера первого
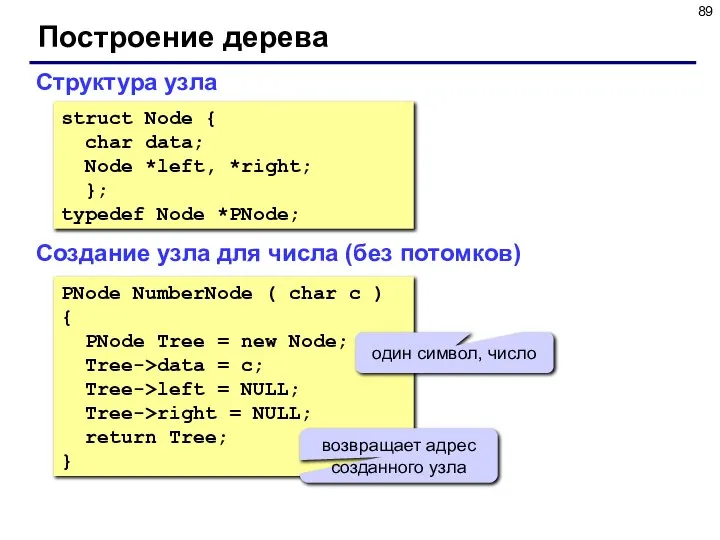
- 89. Построение дерева Структура узла struct Node { char data; Node *left, *right; }; typedef Node *PNode;
- 90. Построение дерева //-------------------------------------------- // Функция MakeTree – построение дерева // Вход: строка, номера первого и последнего
- 91. Вычисление выражения по дереву //-------------------------------------------- // Функция CalcTree – вычисление по дереву // Вход: адрес дерева
- 92. Основная программа //-------------------------------------------- // Основная программа: ввод и вычисление // выражения с помощью дерева //-------------------------------------------- void
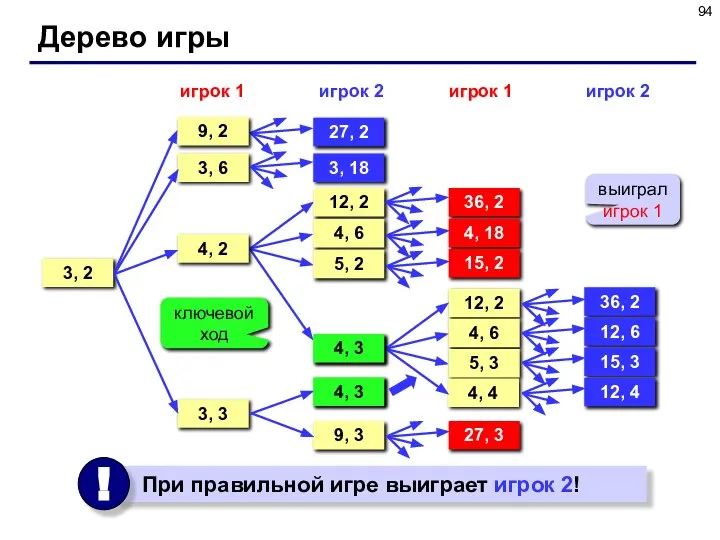
- 93. Дерево игры Задача. Перед двумя игроками лежат две кучки камней, в первой из которых 3, а
- 94. Дерево игры 3, 2 игрок 1 3, 6 27, 2 3, 18 3, 3 4, 2
- 95. Задания «4»: «Собрать» программу для вычисления правильного арифметического выражения, включающего только однозначные числа и знаки операций
- 96. Тема 7. Графы © К.Ю. Поляков, 2008 Динамические структуры данных (язык Си)
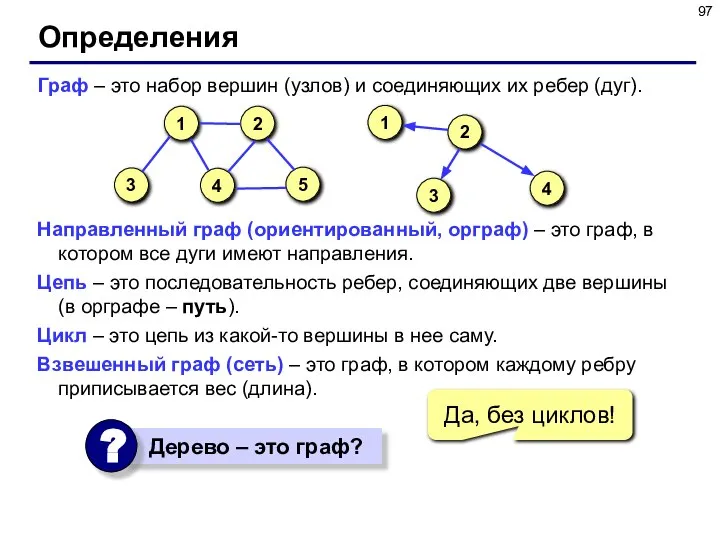
- 97. Определения Граф – это набор вершин (узлов) и соединяющих их ребер (дуг). Направленный граф (ориентированный, орграф)
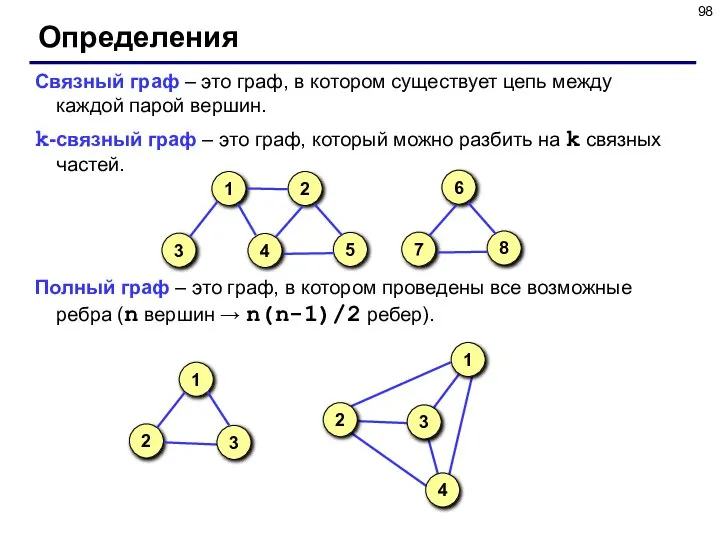
- 98. Определения Связный граф – это граф, в котором существует цепь между каждой парой вершин. k-cвязный граф
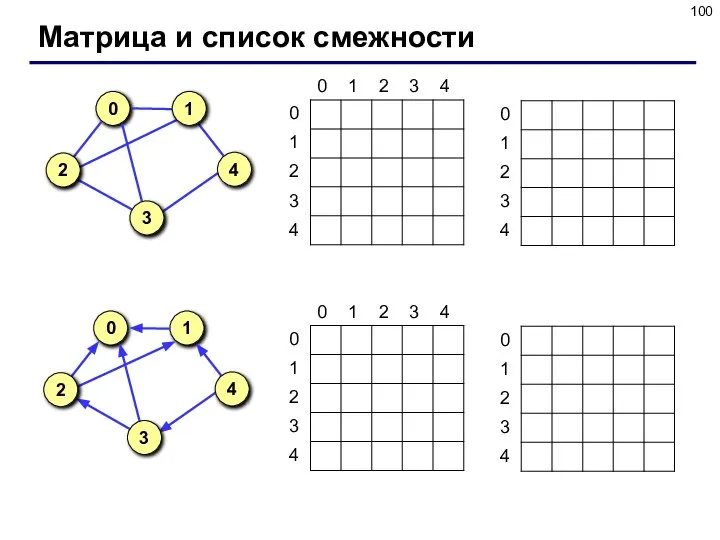
- 99. Описание графа Матрица смежности – это матрица, элемент M[i][j] которой равен 1, если существует ребро из
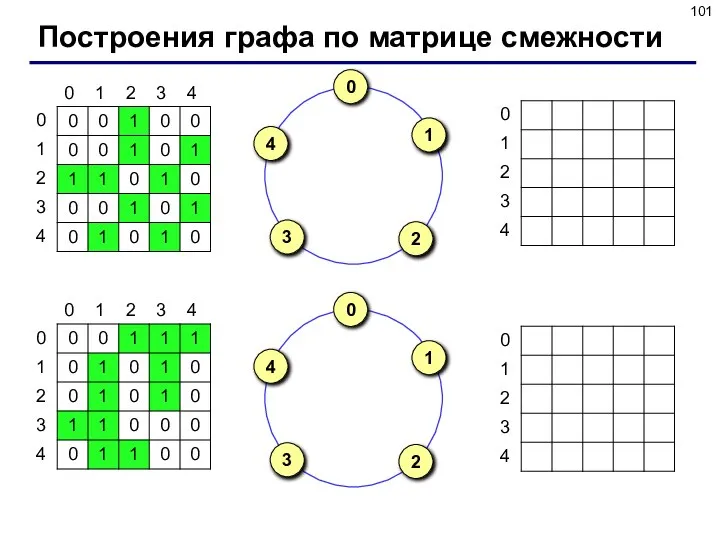
- 100. Матрица и список смежности
- 101. Построения графа по матрице смежности
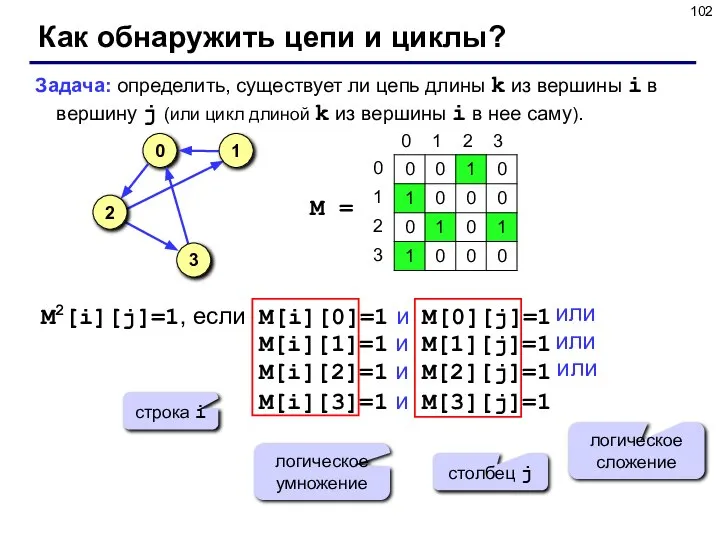
- 102. Как обнаружить цепи и циклы? Задача: определить, существует ли цепь длины k из вершины i в
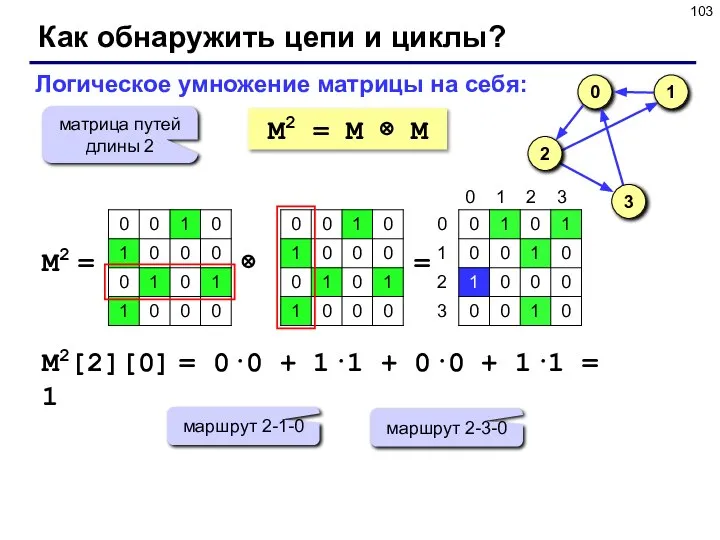
- 103. Как обнаружить цепи и циклы? M2 = M ⊗ M Логическое умножение матрицы на себя: матрица
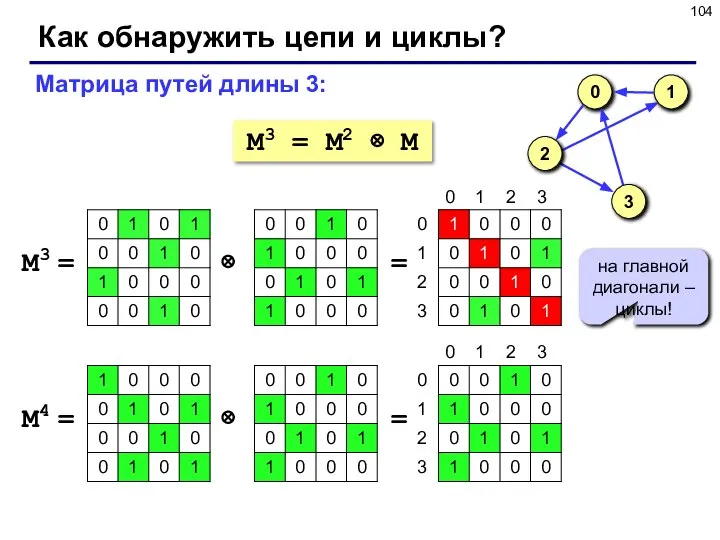
- 104. Как обнаружить цепи и циклы? M3 = M2 ⊗ M Матрица путей длины 3: M3 =
- 105. Весовая матрица Весовая матрица – это матрица, элемент W[i][j] которой равен весу ребра из вершины i
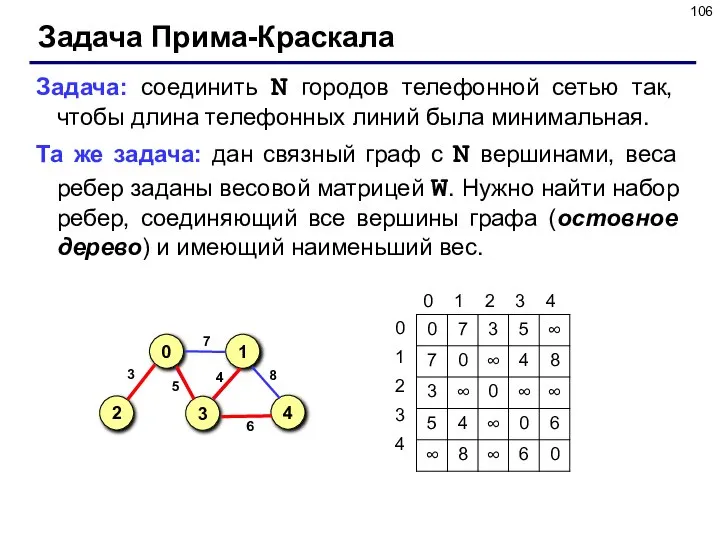
- 106. Задача Прима-Краскала Задача: соединить N городов телефонной сетью так, чтобы длина телефонных линий была минимальная. Та
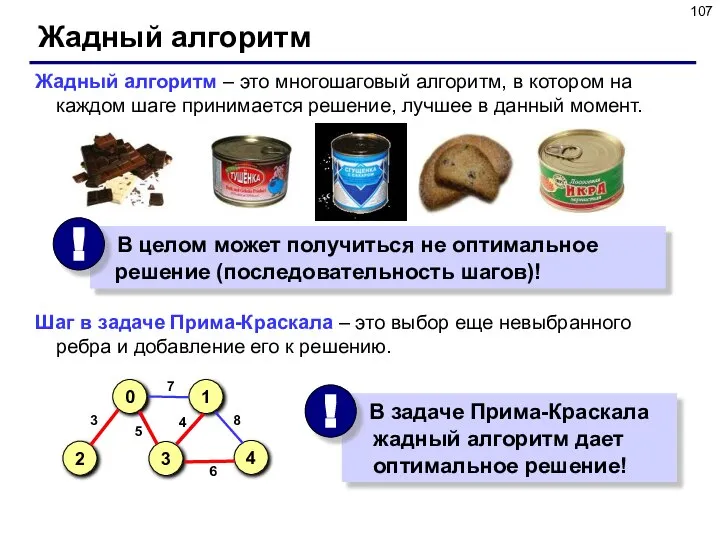
- 107. Жадный алгоритм Жадный алгоритм – это многошаговый алгоритм, в котором на каждом шаге принимается решение, лучшее
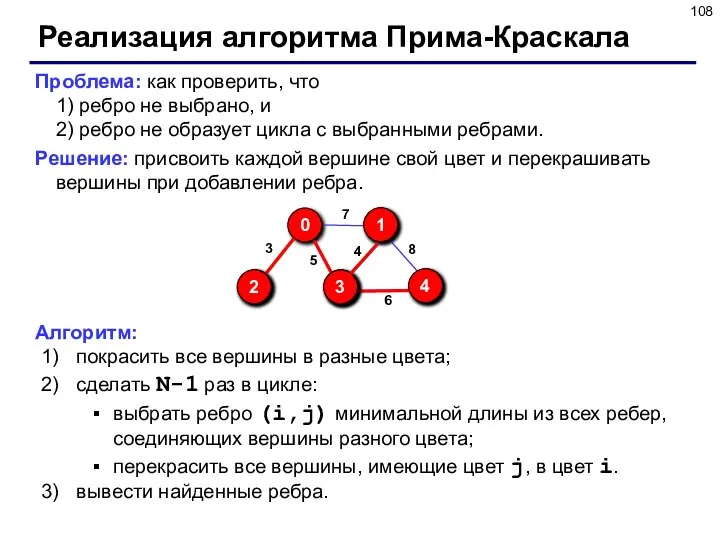
- 108. Реализация алгоритма Прима-Краскала Проблема: как проверить, что 1) ребро не выбрано, и 2) ребро не образует
- 109. Реализация алгоритма Прима-Краскала Структура «ребро»: struct rebro { int i, j; // номера вершин }; const
- 110. Реализация алгоритма Прима-Краскала for ( k = 0; k min = 30000; // большое число for
- 111. Сложность алгоритма Основной цикл: O(N3) for ( k = 0; k ... for ( i =
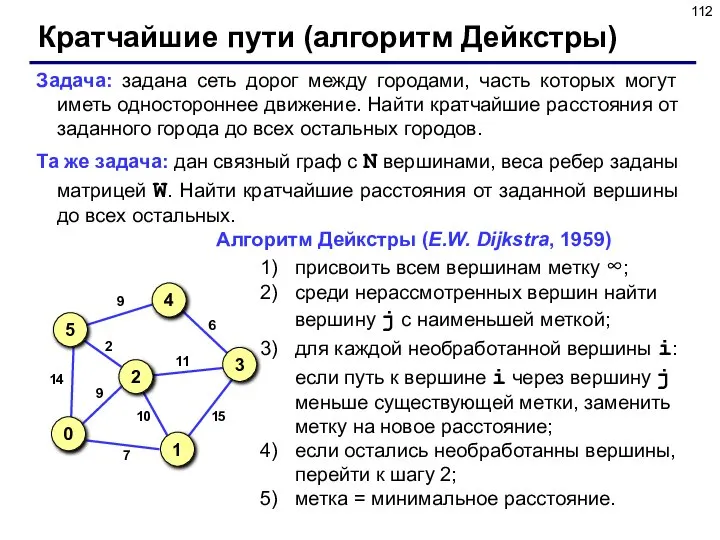
- 112. Кратчайшие пути (алгоритм Дейкстры) Задача: задана сеть дорог между городами, часть которых могут иметь одностороннее движение.
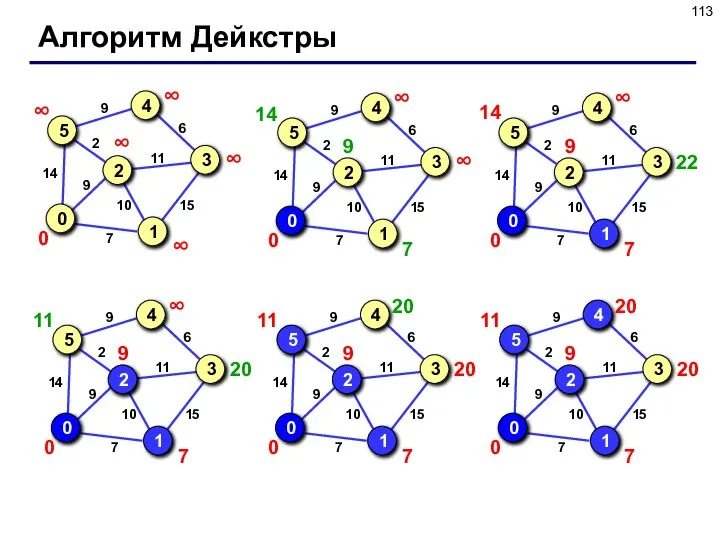
- 113. Алгоритм Дейкстры
- 114. Реализация алгоритма Дейкстры Массивы: массив a, такой что a[i]=1, если вершина уже рассмотрена, и a[i]=0, если
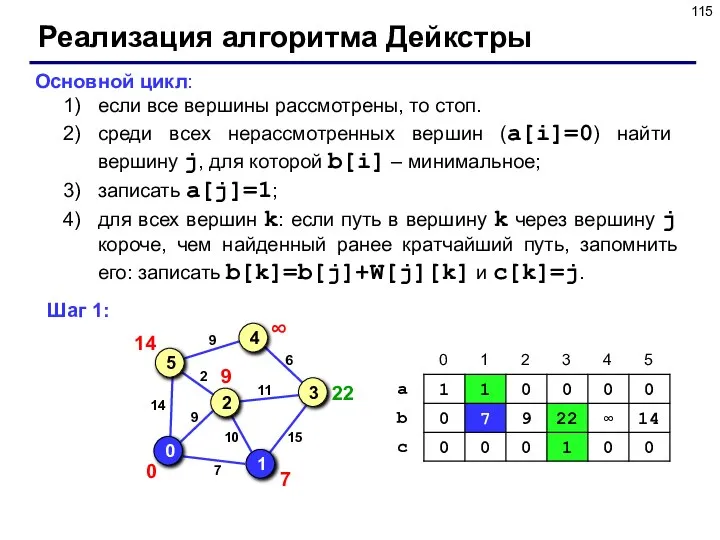
- 115. Реализация алгоритма Дейкстры Основной цикл: если все вершины рассмотрены, то стоп. среди всех нерассмотренных вершин (a[i]=0)
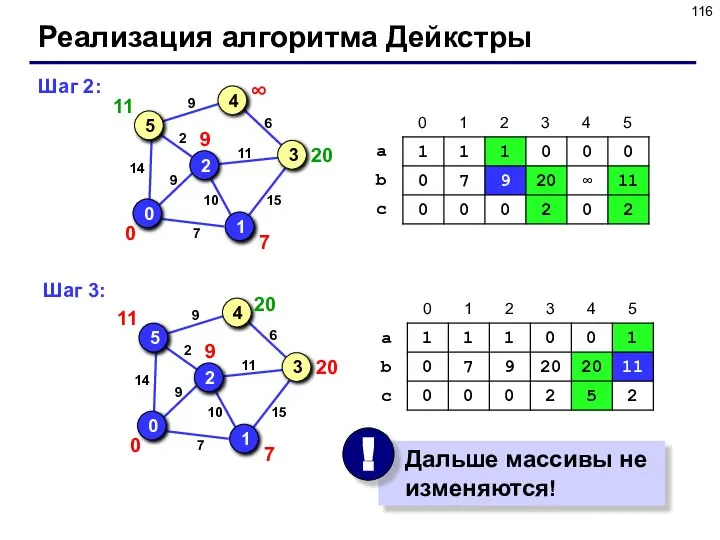
- 116. Реализация алгоритма Дейкстры Шаг 2: Шаг 3:
- 117. Как вывести маршрут? Результат работа алгоритма Дейкстры: длины путей Маршрут из вершины 0 в вершину 4:
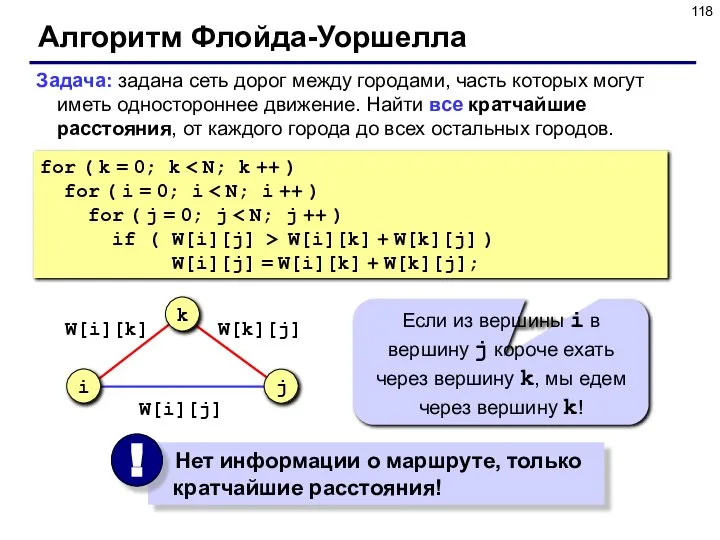
- 118. Алгоритм Флойда-Уоршелла Задача: задана сеть дорог между городами, часть которых могут иметь одностороннее движение. Найти все
- 119. Алгоритм Флойда-Уоршелла Версия с запоминанием маршрута: for ( i = 0; i for ( j =
- 120. Задача коммивояжера Задача коммивояжера. Коммивояжер (бродячий торговец) должен выйти из первого города и, посетив по разу
- 121. Другие классические задачи Задача на минимум суммы. Имеется N населенных пунктов, в каждом из которых живет
- 123. Скачать презентацию











![Вариант 2. Один блок на матрицу A Выделение памяти: A[0] ... A[M]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1118775/slide-15.jpg)




![Массивы структур Объявление: Book B[10]; Обращение к полям: for ( i =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1118775/slide-20.jpg)



![Реализация в программе const N = 10; Book B[N]; Book *p[N], *temp;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1118775/slide-25.jpg)



![Создание узла PNode CreateNode ( char NewWord[] ) { PNode NewNode =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1118775/slide-31.jpg)



![Двусвязные списки Структура узла: struct Node { char word[40]; // слово int](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1118775/slide-42.jpg)





![Программа void main() { char br1[3] = { '(', '[', '{' };](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1118775/slide-50.jpg)

























![Описание графа Матрица смежности – это матрица, элемент M[i][j] которой равен 1,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1118775/slide-98.jpg)
![Весовая матрица Весовая матрица – это матрица, элемент W[i][j] которой равен весу](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1118775/slide-104.jpg)



![Реализация алгоритма Дейкстры Массивы: массив a, такой что a[i]=1, если вершина уже](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1118775/slide-113.jpg)




 Программирование и безопасность баз данных мобильных систем. Лекция 3
Программирование и безопасность баз данных мобильных систем. Лекция 3 Исполнитель Робот. Сложные условия
Исполнитель Робот. Сложные условия Основные этапы информатизации общества
Основные этапы информатизации общества Internet of Things
Internet of Things Социальные сети: предпосылки появления и особенности развития
Социальные сети: предпосылки появления и особенности развития Электронные больничные. СБИС+
Электронные больничные. СБИС+ Виды компьютерных систем
Виды компьютерных систем Системы счисления
Системы счисления Инновационные технологии как средство достижения планируемых результатов
Инновационные технологии как средство достижения планируемых результатов Создание SQL запросов в MS Access для манипулирования данными
Создание SQL запросов в MS Access для манипулирования данными Описание модели приложения с помощью UML
Описание модели приложения с помощью UML Сучасні операційні системи
Сучасні операційні системи Технологии глобальных сетей
Технологии глобальных сетей 1C: Предприятия. Оценка персонала
1C: Предприятия. Оценка персонала Кодирование информации. Декодирование слов по номерам букв
Кодирование информации. Декодирование слов по номерам букв Языки программирования. Позднее и раннее связывание. Полиморфизм. Основные понятия
Языки программирования. Позднее и раннее связывание. Полиморфизм. Основные понятия Руководство по регистрации в ЭБС Букап для пользователей институтов
Руководство по регистрации в ЭБС Букап для пользователей институтов Библиотеки Python
Библиотеки Python Классификация языков программирования. Структура программы на С#. Первая программа
Классификация языков программирования. Структура программы на С#. Первая программа Регистровая память. Регистры микропроцессора
Регистровая память. Регистры микропроцессора Защита объектов информатизации от хакерских атак
Защита объектов информатизации от хакерских атак Кластер. Как составить кластер
Кластер. Как составить кластер Инструкция на получение сертификата pfdo.e-mordovia.ru
Инструкция на получение сертификата pfdo.e-mordovia.ru Копирайт и картинки. Midea team 2021
Копирайт и картинки. Midea team 2021 Программное обеспечение для параметрического представления границ
Программное обеспечение для параметрического представления границ Циклы. Цикл for
Циклы. Цикл for Архитектура, назначение и функции операционных систем. Введение в теорию операционных систем. Занятие 1.1
Архитектура, назначение и функции операционных систем. Введение в теорию операционных систем. Занятие 1.1 Интерфейсы на Java
Интерфейсы на Java