Формализация понятия Алгоритм

кафедра ЮНЕСКО по НИТ
Постановка проблемы
Определение алгоритма, можно назвать понятием алгоритма в интуитивном смысле.
Свойства алгоритмов следует называть эмпирическими. Однако, как фундаментальное научное понятие алгоритм требует более обстоятельного изучения. Оно невозможно без уточнения понятия «алгоритм», более строгого его описания или, как еще говорят, без его формализации.
Известно несколько подходов к формализации понятия «алгоритм»:
теория конечных и бесконечных автоматов;
теория вычислимых (рекурсивных) функций;
λ-исчисление Черча.

кафедра ЮНЕСКО по НИТ
Постановка проблемы
Главная цель формализации понятия алгоритма такова: подойти к решению проблемы алгоритмической разрешимости различных математических задач, т.е. ответить на вопрос, может ли быть построен алгоритм, приводящий к решению задачи.
Вместе с тем, формально, определенный любым из известных способов, алгоритм не может в практическом программировании заменить то, что мы называли алгоритмами в предыдущей лекции. Основная причина состоит в том, что формальное определение резко сужает круг рассматриваемых задач, делая многие практически важные задачи недоступными для рассмотрения.

кафедра ЮНЕСКО по НИТ
История
Машины Поста и Тьюринга, предназначенные для доказательств различных утверждений о свойствах программ для них, были предложены независимо друг от друга в 1936 г. американским математиком Эмилем Постом и английским математиком Алланом Тьюрингом.
Эти машины представляют собой универсальных исполнителей, являющихся полностью детерминированными, позволяющих «вводить» начальные данные, и после выполнения программ «читать» результат. Машина Поста менее популярна, хотя она значительно проще машины Тьюринга. С ее помощью можно вести обучение первым навыкам составления программ для ЭВМ.

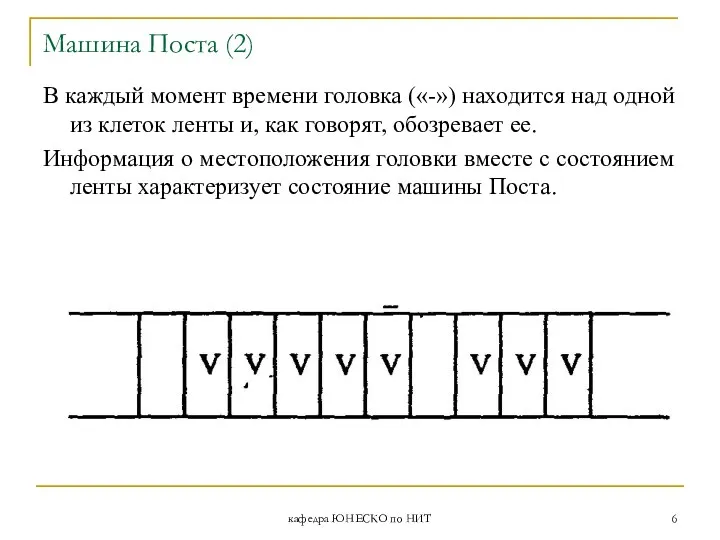
кафедра ЮНЕСКО по НИТ
Машина Поста
Абстрактная машина Поста представляет собой бесконечную ленту, разделенную на одинаковые клетки, каждая из которых может быть либо пустой, либо заполненной меткой «V», и головки, которая может перемещаться вдоль ленты на одну клетку вправо или влево, наносить в клетку ленты метку, если этой метки там ранее не было, стирать метку, если она была, или проверять наличие в клетке метки.
Информация о заполненных метками клетках ленты характеризует состояние ленты, которое может меняться в процессе работы машины.

кафедра ЮНЕСКО по НИТ
Машина Поста (2)
В каждый момент времени головка («-») находится над одной из клеток ленты и, как говорят, обозревает ее.
Информация о местоположения головки вместе с состоянием ленты характеризует состояние машины Поста.

кафедра ЮНЕСКО по НИТ
Команда машины Поста
Структура команды:
п Km,
где
п - порядковый номер команды,
K-действие, выполняемое головкой,
т - номер следующей команды, подлежащей выполнению.
Существует всего шесть команд машины Поста.

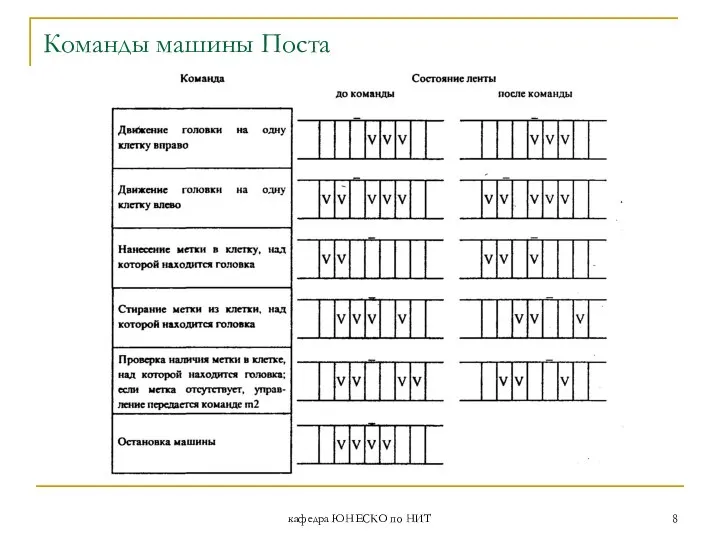
кафедра ЮНЕСКО по НИТ
Команды машины Поста

кафедра ЮНЕСКО по НИТ
Машина Поста
Программой для машины Поста будем называть непустой список команд, такой что 1) на п-м месте команда с номером n; 2) номер т каждой команды совпадает с номером какой-либо команды списка.
С точки зрения свойств алгоритмов, изучаемых с помощью машины Поста, наибольший интерес представляют причины останова машины при выполнении программы:
1) останов по команде «стоп»; такой останов называется результативным и указывает на корректность алгоритма (программы);
2) останов при выполнении недопустимой команды; в этом случае останов называется безрезультативным;
3) машина не останавливается никогда; в этом и в предыдущем случае мы имеем дело с некорректным алгоритмом (программой).
Будем понимать под начальным состояние расположение головки против пустой клетки левее самой левой метки на ленте.

кафедра ЮНЕСКО по НИТ
Машина Поста. Пример №1.
Пусть задано исходное состояние головки и требуется на пустой ленте написать две метки: одну в секцию под головкой, вторую справа от нее.

кафедра ЮНЕСКО по НИТ
Машина Поста. Пример №2.
Покажем, как можно воспользоваться командой условного перехода для организации циклического процесса. Пусть на ленте имеется запись из нескольких меток подряд и головка находится над самой крайней меткой справа. Требуется перевести головку влево до первой пустой позиции. .

кафедра ЮНЕСКО по НИТ
Машина Поста. Пример №3.
Представлении чисел на ленте машины Поста и выполнении операций над ними.
Число k представляется на ленте машины Поста идущими подряд k + 1 метками (одна метка означает число «О»). Между двумя числами делается интервал как минимум из одной пустой секции на ленте. Например, запись чисел 3 и 5 на ленте машины Поста будет выглядеть так:
Обратим внимание, что используемая в машине Поста система записи чисел является непозиционной.

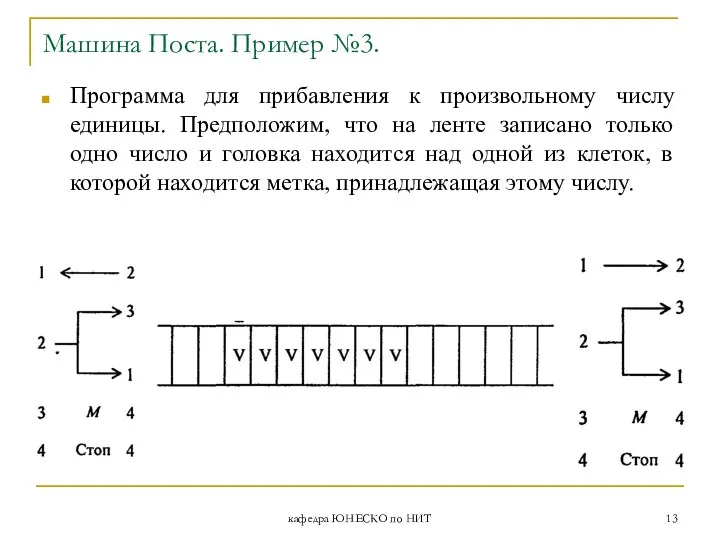
кафедра ЮНЕСКО по НИТ
Машина Поста. Пример №3.
Программа для прибавления к произвольному числу единицы. Предположим, что на ленте записано только одно число и головка находится над одной из клеток, в которой находится метка, принадлежащая этому числу.

кафедра ЮНЕСКО по НИТ
Машина Поста.
Машину Поста можно рассматривать как упрощенную модель ЭВМ.
В самом деле, как ЭВМ, так и машина Поста имеют:
неделимые носители информации (клетки - биты), которые могут быть заполненными или незаполненными;
ограниченный набор элементарных действий - команд, каждая из которых выполняется за один такт (шаг).
Обе машины работают на основе программы. Однако, в машине Поста информация располагается линейно и читается подряд, а в ЭВМ можно читать информацию по адресу; набор команд ЭВМ значительно шире и выразительнее, чем команды машины Поста и т.д.

кафедра ЮНЕСКО по НИТ
Машина Тьюринга

кафедра ЮНЕСКО по НИТ
Машина Тьюринга
Машина Тьюринга (МТ) состоит из счетной ленты, читающей и пишущей головки, лентопротяжного механизма и операционного исполнительного устройства, которое может находиться в одном из дискретных состояний q0, q1, ..., qs, принадлежащих некоторой конечной совокупности. При этом q0 называется начальным состоянием.
Читающая и пишущая головка может читать буквы рабочего алфавита А = {а0, a1, ..., аt}, стирать их и печатать. Каждая ячейка ленты в каждый момент времени занята буквой из множества А. Чаще всего встречается буква а0 - «пробел». Головка находится в каждый момент времени над некоторой ячейкой ленты - текущей рабочей ячейкой. Лентопротяжный механизм может перемещать ленту так, что головка оказывается над соседней ячейкой ленты. При этом возможна ситуация выхода за левый край ленты (ЛК), которая является аварийной, или машинного останова (МО), когда машина выполняет предписание об остановке.

кафедра ЮНЕСКО по НИТ
Машина Тьюринга
Порядок работы МТ (с рабочим алфавитом а0, a1, ..., аt и состояниями q0, q1, ..., qs) описывается таблицей машины Тьюринга. Эта таблица является матрицей с четырьмя столбцами и (s + 1) (t + 1) строками.
Каждая строка имеет вид

кафедра ЮНЕСКО по НИТ
Машина Тьюринга
Здесь:
vij обозначен элемент объединения алфавита {а0, a1, ..., аt} и множества предписаний для лентопротяжного механизма: l - переместить ленту влево, r -переместить ленту вправо, s - остановить машину;
vij - действие МТ, состоящее либо в занесении в ячейку ленты символа алфавита а0, a1, ..., аt, либо в движении головки, либо в останове машины; qij является последующим состоянием.

кафедра ЮНЕСКО по НИТ
Работа машины Тьюринга
МТ работает согласно следующим правилам:
если МТ находится в состоянии qi, головка прочитывает символ 0 в рабочей ячейке. Пусть строка qi аj vij qij, начинающаяся с символов qi, аj, встречается только один раз в таблице.
Если vij - буква рабочего алфавита, то головка стирает содержимое рабочей ячейки и заносит туда эту букву.
Если vij - команда r или l для лентопротяжного механизма, то лента сдвигается на одну ячейку вправо или влево (если не происходит выход за левый край ленты) соответственно.
Если vij =s, то происходит машинный останов.

кафедра ЮНЕСКО по НИТ
Машина Тьюринга. Пример №1.
Алгоритм прибавления единицы к числу п в десятичной системе счисления. Дана десятичная запись числа п; требуется получить десятичную запись числа п + 1.
Очевидно, что внешний алфавит МТ должен состоять из десяти цифр 0,1,2,3,4,5,6,7,8,9 и символа пробела _. Эти цифры записывают по одной в ячейке (подряд, без пропусков).
Оказывается достаточным иметь два внутренних состояния машины: q1 и q2.
Предположим, что в начальный момент головка находится над одной из цифр числа, а машина находится в состоянии q1. Тогда задача может быть решена в два этапа: движения головки к цифре единиц числа (во внутреннем состоянии q1) и замене этой цифры на единицу большую (с учетом переноса 1 в следующий разряд, если это 9, во внутреннем состоянии q2. Соответствующая схема МТ может иметь вид

кафедра ЮНЕСКО по НИТ
Машина Тьюринга. Пример №1.

кафедра ЮНЕСКО по НИТ
Нормальные алгоритмы Маркова
Рассмотрим некоторые понятия ассоциативного исчисления. Пусть имеется алфавит (конечный набор различных символов). Составляющие его символы будем называть буквами. Любая конечная последовательность букв алфавита (линейный их ряд) называется словом в этом алфавите.
Рассмотрим два слова N и М в некотором алфавите А. Если N является частью М, то говорят, что N входит в М.
Зададим в некотором алфавите конечную систему подстановок N - М, S - Т,..., где N, М, S, Т,... - слова в этом алфавите. Любую подстановку N-M можно применить к некоторому слову К следующим способом: если в К имеется одно или несколько вхождений слова N, то любое из них может быть заменено словом М, и, наоборот, если имеется вхождение М, то его можно заменить словом N.
Например, в алфавите А = {а, b, с} имеются слова N = ab, М = bcb, К = abcbcbab, Заменив в слове К слово N на М, получим bcbcbcbab или abcbcbbcb, и, наоборот, заменив М на N, получим aabcbab или аbсаbаb.

кафедра ЮНЕСКО по НИТ
Нормальные алгоритмы Маркова
Подстановка ab - bcb недопустима к слову bacb, так как ни ab, ни bcb не входит в это слово. К полученным с помощью допустимых подстановок словам можно снова применить допустимые подстановки и т.д. Совокупность всех слов в данном алфавите вместе с системой допустимых подстановок называют ассоциативным исчислением. Чтобы задать ассоциативное исчисление, достаточно задать алфавит и систему подстановок.
Слова P1 и Р2 в некотором ассоциативном исчислении называются смежными, если одно из них может быть преобразовано в другое однократным применением допустимой подстановки.
Последовательность слов Р, P1, Р2, ..., М называется дедуктивной цепочкой, ведущей от слова Р к слову М, если каждое из двух рядом стоящих слов этой цепочки - смежное.
Слова Р и М называют эквивалентными, если существует цепочка от Р к М и обратно.

кафедра ЮНЕСКО по НИТ
Нормальные алгоритмы Маркова. Пример.
Алфавит Подстановки
{а, b, с, d, е} ас - сa, abac - abace
ad - da; eca - ae
bc - cb; eda - be
bd - db; edb - be

кафедра ЮНЕСКО по НИТ
Нормальные алгоритмы Маркова
Нормальные алгоритмы Маркова являются не только средством теоретических построений, но и основой специализированного языка программирования, применяемого как язык символьных преобразований при разработке систем искусственного интеллекта. Это один из немногих языков, разработанных в России и получивших известность во всем мире.
Существует строгое доказательство того, что по возможностям преобразования нормальные алгоритмы Маркова эквивалентны машинам Тьюринга.

кафедра ЮНЕСКО по НИТ
Рекурсивные функции
Еще одним подходом к проблеме формализации понятия алгоритма являются, так называемые, рекурсивные функции.
Рекурсией называется способ задания функции, при котором значение функции при определенном значении аргументов выражается через уже заданные значения функции при других значениях аргументов. Применение рекурсивных функций в теории алгоритмов основано на идее нумерации слов в произвольном алфавите последовательными натуральными числами. Таким образом любой алгоритм можно свести к вычислению значений некоторой целочисленной функции при целочисленных значениях аргументов.

кафедра ЮНЕСКО по НИТ
Рекурсивные функции. Основные понятия.
Пусть X, Y - два множества. Частичной функцией (или отображением) из Х в Y будем называть пару
, состоящую из подмножества D(f) ⊂ X (называемого областью определения f) и отображения f: D(f) → Y. Если D(f) пусто, то f нигде не определена. Будем считать, что существует единственная нигде не определенная частичная функция.