Слайд 2Формы мышления
Первые учения о формах и способах рассуждений возникли в странах Древнего Востока (Китай, Индия),

но в основе современной логики лежат учения, созданные в 4 веке до нашей эры древне-греческими мыслителями.
Основы формальной логики заложил Аристотель, который впервые отделил логические формы речи от ее содержания. Он исследовал терминологию логики, подробно разобрал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления.
Логика изучает внутреннюю структуру процесса мышления, который реализуется в таких естественно сложившихся формах как понятие, суждение, умозаключение и доказательство.
Слайд 3Понятие
Понятие - это форма мышления, отражающая наиболее существенные свойства предмета, отличающие его от

других предметов.
В структуре каждого понятия нужно различать две стороны: содержание и объем.
Содержание понятия составляет совокупность существенных признаков предмета. Объем понятия определяется совокупностью предметов, на которую оно распространяется.
Слайд 4Высказывание.
Высказывание (суждение) - это форма мышления, выраженная с помощью понятий, посредством которой

что-либо утверждают или отрицают о предметах, их свойствах и отношениях между ними.
Высказывание может быть истинным или ложным. Истинным будет суждение, в котором связь понятий правильно отражает свойства и отношения реальных вещей. Ложным суждение будет в том случае, когда связь понятий искажает объективные отношения, не соответствует реальной действительности.
В естественном языке высказывания выражаются повествовательными предложениями. Высказывание не может быть выражено повелительным или вопросительным предложением. Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков.
Высказывание называется простым, если никакая его часть сама не является высказыванием. Высказывание, состоящее из простых высказываний, называются составным (сложным).
Слайд 5Умозаключение.
Умозаключение - это форма мышления, посредством которой из одного или нескольких суждений,

называемых посылками, по определенным правилам логического вывода получается новое знание о предметах реального мира (вывод).
Умозаключения бывают дедуктивные, индуктивные и по аналогии. В дедуктивных умозаключениях рассуждения ведутся от общего к частному. Например, из двух суждений: «Все металлы электропроводны» и «Ртуть является металлом» путем умозаключения можно сделать вывод, что: «Ртуть электропроводна».
В индуктивных умозаключениях рассуждения ведутся от частного к общему. Например, установив, что отдельные металлы - железо, медь, цинк, алюминий и т.д. - обладают свойством электропроводности, можно сделать вывод, что все металлы электропроводны.
Умозаключение по аналогии представляет собой движение мысли от общности одних свойств и отношений у сравниваемых предметов или процессов к общности других свойств и отношений. Например, химический состав Солнца и Земли сходен по многим показателям, поэтому, когда на Солнце обнаружили неизвестный еще на Земле химический элемент гелий, то по аналогии заключили: такой элемент есть и на Земле.
Слайд 6Доказательство.
Доказательство есть мыслительный процесс, направленный на подтверждение или опровержение какого-либо положения посредством других несомненных,

ранее обоснованных доводов.
Доказательство по своей логической форме не отличается от умозаключения. Однако, если в умозаключении заранее исходят из истинности посылок и следят только за правильностью логического вывода, в доказательстве подвергается логической проверке истинность самих посылок.
Слайд 7Алгебра высказываний
Алгебра в широком смысле этого слова наука об общих операциях, аналогичных сложению и

умножению, которые могут выполняться над различными математическими объектами (алгебра переменных и функций, алгебра векторов, алгебра множеств и т.д.).
Объектами алгебры логики являются высказывания.
Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт — истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами.
Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:
А = {Аристотель - основоположник логики}
В = {На яблонях растут бананы}.
Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом, А = 1, В = 0.
Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре высказываний заменяются на логические операции. Логические операции задаются таблицами истинности
Слайд 8Логическая операция КОНЪЮНКЦИЯ (логическое умножение):
· в естественном языке соответствует союзу и;
· в алгебре высказываний обозначение &,^;
· в

языках программирования обозначение And.
Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Слайд 9Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение):
· в естественном языке соответствует союзу или;
· обозначение V ;
· в языках программирования

обозначение Or.
Дизъюнкция - это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
Слайд 10Логическая операция ИНВЕРСИЯ
(отрицание):
в естественном языке соответствует словам неверно, что... и частице не;
· обозначение ¬,¯ ;
· в языках

программирования обозначение Not;
Отрицание - это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
Слайд 11Логическая операция ИМПЛИКАЦИЯ
(логическое следование):

Слайд 12Логическая операция ЭКВИВАЛЕНТНОСТЬ
(равнозначность):

Слайд 13Логические выражения и таблицы истинности
Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях

(наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания.
Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности.
Слайд 14Логические выражения и таблицы истинности
Алгоритм построения таблицы истинности:
1) подсчитать количество переменных n в логическом выражении;
2) определить число строк

в таблице, которое равно m = 2n;
3) подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество операций;
4) ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;
5) заполнить стобцы входных переменных наборами значений;
6) провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в п.4 последовательностью.
Слайд 15Логические выражения и таблицы истинности
Наборы входных переменных, во избежание ошибок, рекомендуют перечислять

следующим образом:
а) разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю единицами;
б) разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами нулей и единиц , начиная с группы нулей;
в) продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами нулей или единиц до тех пор, пока группы нулей и единиц не будут состоять из одного символа.
Слайд 16Пример
Для формулы A^(B V(¬B^ ¬C) ) построить таблицу истинности алгебраически и с использованием электронных таблиц.
Количество логических переменных

3, следовательно, количество строк в таблице истинности должно быть 23 = 8.
Количество логических операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3 + 5 = 8.
Слайд 17Логические функции
Логической (булевой) функцией называют функцию F(Х1, Х2, ..., Хn), аргументы которой Х1, Х2, ..., Хn (независимые переменные) и сама функция (зависимая

переменная) принимают значения 0 или 1.
Таблицу, показывающую, какие значения принимает логическая функция при всех сочетаниях значений ее аргументов, называют таблицей истинности логической функции. Таблица истинности логической функции n аргументов содержит 2n строк, n столбцов значений аргументов и 1 столбец значений функции.
Логические функции могут быть заданы табличным способом или аналитически — в виде соответствующих формул.
Слайд 18Логические законы и правила преобразования логических выражений
1. Закон двойного отрицания:
А=¬¬A.
Двойное отрицание исключает

отрицание.
2. Переместительный (коммутативный) закон:
— для логического сложения:
АVB=BVA;
— для логического умножения:
A^B = B^A.
Слайд 19Логические законы и правила преобразования логических выражений
3. Сочетательный (ассоциативный) закон:
— для логического сложения:
(A VB) VC = A V (B VC);
— для

логического умножения:
(A^B)^C = A^(B^C).
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
4. Распределительный (дистрибутивный) закон:
— для логического сложения:
(AV B)^C = (A^C) V(B^C);
— для логического умножения:
(A^B) VC = (AV C)^(BV C).
Определяет правило выноса общего высказывания за скобку.
Слайд 20Логические законы и правила преобразования логических выражений
5.Закон общей инверсии (законы де Моргана):
—

для логического сложения
¬(AVB)=¬A^¬B;
— для логического умножения:
¬(A^B)=¬AV¬B
Слайд 21Логические законы и правила преобразования логических выражений
6.Закон идемпотентности ( от латинских слов

idem — тот же самый и potens —сильный; дословно — равносильный):
— для логического сложения:
AVA=A;
— для логического умножения:
A^A=A.
Закон означает отсутствие показателей степени.
7.Законы исключения констант:
— для логического сложения:
AV1 = 1, AV0 =A;
— для логического умножения:
A^1 =A, A^0 = 0.
Слайд 22Логические законы и правила преобразования логических выражений
8.Закон противоречия:
A^¬A= 0.
Невозможно, чтобы противоречащие высказывания

были одновременно истинными.
9.Закон исключения третьего:
AÚ¬A= 1.
Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
Слайд 23Логические законы и правила преобразования логических выражений
10.Закон поглощения:
— для логического сложения:
AV(A^B) =A;
—

для логического умножения:
A^(AVB) =A.
11. Закон исключения (склеивания):
— для логического сложения:
(A^B)V(¬A^B) =B;
— для логического умножения:
(AVB)^(¬AVB) =B.






















 Тексти і текстовий редактор. Середовище текстового редактора. Правила введення тексту. Збереження текстового документа
Тексти і текстовий редактор. Середовище текстового редактора. Правила введення тексту. Збереження текстового документа Управление исполнителем Чертёжник
Управление исполнителем Чертёжник Программирование на языке Python. Символьные строки
Программирование на языке Python. Символьные строки Компьютердің қауіпсіздік ережелері
Компьютердің қауіпсіздік ережелері Основные методы обеспечения качества функционирования
Основные методы обеспечения качества функционирования Новые функции программы Zone 3. Полное CAD программирование
Новые функции программы Zone 3. Полное CAD программирование Защита информации, антивирусная защита
Защита информации, антивирусная защита Внеклассное мероприятие. Викторина Информатика и логика
Внеклассное мероприятие. Викторина Информатика и логика Понятие о системах поддержки принятия решений и экспертных системах
Понятие о системах поддержки принятия решений и экспертных системах Отчёт ЛР1 (2)
Отчёт ЛР1 (2) Презентация "Виртуальный читальный зал" - скачать презентации по Информатике
Презентация "Виртуальный читальный зал" - скачать презентации по Информатике Программа Воркшопа. Как подготовить публичное выступление
Программа Воркшопа. Как подготовить публичное выступление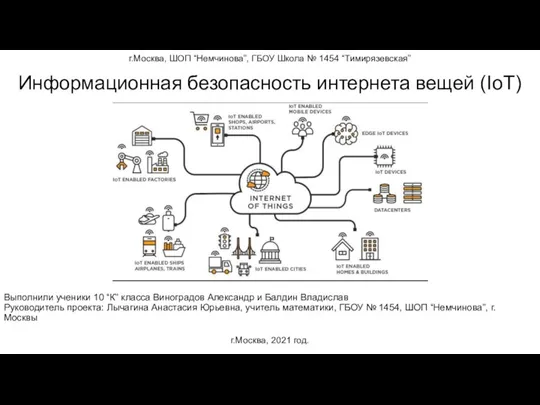 Информационная безопасность интернета вещей (IoT)
Информационная безопасность интернета вещей (IoT) Main features of HTML5
Main features of HTML5 Boolean Algebra
Boolean Algebra Интернет-культура и библиотечные блоги как основа работы со школьниками в ее формировании
Интернет-культура и библиотечные блоги как основа работы со школьниками в ее формировании Современные методы описания функциональных требований к системам. Алистер Коберн
Современные методы описания функциональных требований к системам. Алистер Коберн Программа для создания текстовых документов
Программа для создания текстовых документов Работа с электронной почтой в сети интернет
Работа с электронной почтой в сети интернет Основные каналы взаимодействия с внешним миром
Основные каналы взаимодействия с внешним миром Программирование в среде RobоtC
Программирование в среде RobоtC Информационные системы и технологии. Структура дисциплины
Информационные системы и технологии. Структура дисциплины Гиперссылки. Призентации
Гиперссылки. Призентации Проводник пассажирского вагона 3-го разряда с использованием социальной сети ВКонтакте
Проводник пассажирского вагона 3-го разряда с использованием социальной сети ВКонтакте Разработка тестов. Практическая работа № 5
Разработка тестов. Практическая работа № 5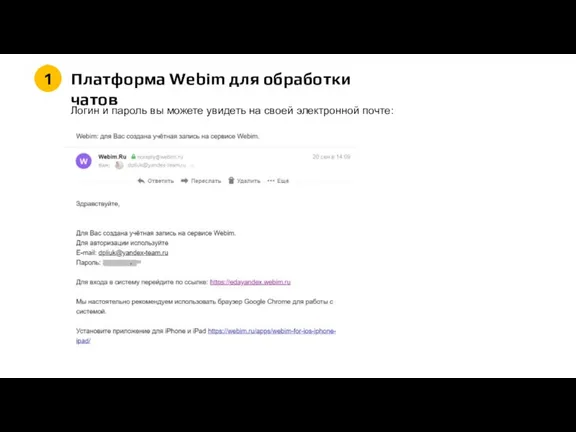 Платформа Webim для обработки чатов
Платформа Webim для обработки чатов Обробка вхідного масиву економічних даних
Обробка вхідного масиву економічних даних Переменные. Оператор присваивания
Переменные. Оператор присваивания