- Главная
- Информатика
- Гибридные криптосистемы защиты информации

Содержание
- 2. 6. Симметричные криптосистемы исследовались в течение десятков и сотен лет, и их безопасность многократно проверялась за
- 3. Достоинства несимметричных криптосистем: 1. Нет необходимости обеспечения секретности всей ключевой информации в несимметричных криптосистемах. 2. Проще
- 4. Недостатки несимметричных криптосистем: 1. Достижимые скорости реализации криптографической защиты информации в несимметричных криптосистемах на несколько порядков
- 5. 5. Безопасность несимметричных криптосистем исследовалась в течение сравнительно малого времени (двадцать лет с момента их возникновения),
- 6. Программа PGP обеспечивает шифрование передаваемых по сети данных, подтверждение подлинности сообщений с помощью цифровой подписи, формирование
- 7. Целостность и авторство передаваемой в PGP информации обеспечивается использованием цифровой подписи сообщений по алгоритму RSA. Пользователь
- 8. Классические протоколы распределения ключей предписывают предварительно рассылать сформированные самими пользователями или центром формирования ключей (ЦФК) ключи
- 9. Поэтому подлинность полученных по каналу связи открытых ключей нового корреспондента подтверждает цифровая подпись того корреспондента, чей
- 10. Достоинством первого является более высокая скорость работы (практически на два порядка быстрее алгоритма RSA) и более
- 11. Одним из основных достоинств PGP является удобство управления ключами. Программа PGP сама формирует пару ключей (открытый
- 12. Для удобства пользования большим количеством ключей каждому ключу –связке поставлен в соответствие уникальный идентификатор, в качестве
- 13. Однонаправленная функция с потайным ходом на основе алгебраических уравнений по модулю 2 Для построения ОНФ с
- 14. Для законного получателя, знающего К, ОНФ обратима. Получатель рекурсивно восстанавливает входной вектор М из полученной криптограммы
- 15. Это-NPсложная задача. Пример. Пусть n=3, f (Ki, Mi)=f(ki1, ki2, ki3; mi1, mi2, mi3)= =(ki1ki2mi1mi2, ki2ki3mi1mi3, (ki1+ki2)mi1mi3)
- 16. К настоящему времени предложено большое количество ОНФ с пх, построенных на основе вычислительно сложных математических задач.
- 17. КРИПТОГРАФИЧЕСКИЕ ХЭШ-ФУНКЦИИ Криптографические хэш-функции (КХФ) в настоящее время широко используются для решения многих задач обеспечения безопасности
- 18. Хэш-функции (ХФ) произвольного вида принадлежат классу однонаправленных функций без потайного хода. Хэш-функции отличаются от прочих функций
- 19. Идея хэширования сообщений заключается в следующем. Пусть множество информационных сообщений {X} составляет словарь S объемом |
- 20. Если I(h,S)=0, то коллизий не происходит, каждое сообщение хэшируется в свой, отличный от других, хэш-код. Хэш-функции,
- 21. Хэширующие функции обычно ведут себя как случайные функции: распределение хэш-кодов равновероятно и практически отсутствует статистическая зависимость
- 22. хэшируется в такое же значение хэш-функции, как любой заданный прообраз, то есть для заданного прообраза X
- 23. классификация КХФ
- 24. Если в процессе хэширования сообщений используется секретный ключ К, то такая функция Н=h(Х, К) называется криптографической
- 25. стойкой к образованию коллизий и стойкой к вычислению второго прообраза. Иногда используются альтернативные термины –ОНКХФ –
- 26. Если нет – то можно использовать ОКХФ. Стойкость ОНКХФ к вычислению прообраза может оцениваться вычислительной сложностью
- 27. составляет не менее 0.5. Атака нарушителя на хэш-функцию с использованием «парадокса» может быть построена следующим образом:
- 28. Этот метод называется итеративным хэшированием. Сообщение Х делится на t блоков X1,X2,…,Xt длиной по b бит.
- 29. Функция f называется шаговой функцией хэширования (иначе – круговая). Для обеспечения стойкости бесключевой хэш-функции важны выбор
- 30. Т.е. если f м.б. инвертирована менее, чем за 2n операций, то для нахождения второго прообраза для
- 31. Вычисление криптографической хэш-функции методом Уинтерница Использование операции блочного хэширования Е –это вычисление криптограммы Нi как функции
- 32. Е(Х, К1) = Е(Х, К2) Поэтому большинство известных КХФ построено на основе алгоритмов блочного шифрования. Отдельный
- 33. Также известны ОН и УКХФ, основанные на высокой вычислительной сложности задачи факторизации большого составного числа и
- 34. Если последний блок неполный, то слева к нему дописываются нулевые символы до длины блока бит. Дополненное
- 35. На третьем этапе выполняется перемешивающее преобразование Ψ шифрованной последовательности Si с учетом предыдущего значения хэш-кода Hi-1
- 36. Криптографические хэш-функции с секретным ключом. Определение 14: хэш-функция называется КХФ с секретным ключом, если она удовлетворяет
- 37. КХФ с секретным ключом делятся на два класса: основанные на блочных алгоритмах и специально разработанные. Как
- 38. Хi в очередное n-битовое значение хэш-кода Hi, а значение хэш-кода h(X, K) всего сообщения Х определяется
- 40. Скачать презентацию
Слайд 26. Симметричные криптосистемы исследовались в течение десятков и сотен лет, и их
6. Симметричные криптосистемы исследовались в течение десятков и сотен лет, и их

Недостатки симметричных криптосистем:
1. Необходимость обеспечения секретности ключей у всех корреспондентов (пользователей) симметричных криптосистем.
2. Для больших информационных систем возникают трудноразрешимые проблемы безопасной доставки ключей участникам информационного обмена. 3. В информационных сетях со многими корреспондентами необходима частая смена одинаковых для всех ключей (так как криптосвязность обеспечивается, как правило, по принципу общей ключевой сети).
4. Симметричные криптосистемы не способны обеспечить аутентификацию сообщений и объектов в условиях взаимного недоверия и возможного обмана со стороны участников информационного обмена.
Слайд 3Достоинства несимметричных криптосистем:
1. Нет необходимости обеспечения секретности всей ключевой информации в несимметричных
Достоинства несимметричных криптосистем:
1. Нет необходимости обеспечения секретности всей ключевой информации в несимметричных

2. Проще решаются вопросы доставки ключей участникам информационного обмена.
3. Не требуется частой смены ключей пользователей несимметричных криптосистем (так как криптосвязность обеспечивается, как правило, по принципу ключевого направления или сети циркулярной связи).
4. Несимметричные криптосистемы способны обеспечить аутентификацию сообщений и объектов в условиях взаимного недоверия и возможного обмана со стороны участников информационного обмена, причем ключи проверки могут быть очень короткими.
5. В больших информационных сетях для обеспечения криптосвязности участников информационного обмена количество ключей для несимметричных криптосистем может быть значительно меньше, чем для симметричных.
Слайд 4Недостатки несимметричных криптосистем:
1. Достижимые скорости реализации криптографической защиты информации в несимметричных криптосистемах
Недостатки несимметричных криптосистем:
1. Достижимые скорости реализации криптографической защиты информации в несимметричных криптосистемах

2. Размеры ключей для несимметричных криптосистем, как правило, существенно больше, чем для симметричных криптосистем.
3. Современные несимметричные криптосистемы не являются безусловно стойкими, более того, неизвестно ни одной практически реализуемой несимметричной системы шифрования, стойкость которой была бы строго доказана при любых атаках нарушителя.
4. Безопасность известных практически используемых несимметричных криптосистем основана на вычислительной сложности узкого класса теоретико-числовых задач, для которых в будущем могут быть найдены эффективные алгоритмы их решения (взлома криптосистем).
Слайд 55. Безопасность несимметричных криптосистем исследовалась в течение сравнительно малого времени (двадцать лет
5. Безопасность несимметричных криптосистем исследовалась в течение сравнительно малого времени (двадцать лет

Симметричные и несимметричные криптосистемы защиты информации имеют взаимодополняющие достоинства. Симметричные криптосистемы наиболее эффективны для сохранения в тайне защищаемой информации, а несиммет-ричные - для контроля ее подлинности и установления криптосвязности корреспондентов.
Поэтому на практике используют комбинированные криптографические системы защиты информации, называющиеся гибридными криптосистемами.
Примером гибридной криптосистемы защиты информации является популярная в сети Интернет программно-реализованная криптосистема зашиты информации PGP (Pretty Good Privacy), разработанная коллективом специалистов во главе с Ф.Циммерманом.
Слайд 6Программа PGP обеспечивает шифрование передаваемых по сети данных, подтверждение подлинности сообщений с
Программа PGP обеспечивает шифрование передаваемых по сети данных, подтверждение подлинности сообщений с

Для шифрования данных используется алгоритм блочного шифрования IDEA (International data encryption algorithm), разработанный в конце 80-х годов известным криптографом Дж Месси. Как и DES, IDEA шифрует блоки данных длиной 64 бита, но использует более длинные 128-битные ключи, что практически исключает при атаке нарушителя перебор всех ключей алгоритма. Перед шифрованием данных в PGP рекомендуется их сжимать с помощью алгоритма сжатия типа ZIP.
Сжатие избыточной информации целесообразно как с точки зрения снижения требований к пропускной способности используемых каналов связи, так и для существенного повышения криптостойкости алгоритмов шифрования благодаря удалению избыточности шифруемой информации
Слайд 7Целостность и авторство передаваемой в PGP информации обеспечивается использованием цифровой подписи сообщений
Целостность и авторство передаваемой в PGP информации обеспечивается использованием цифровой подписи сообщений

В качестве криптографической функции хеширования при подписи сообщения используется функция MD5, сжимающая подписываемое сообщение произвольного размера в хэш-код длиною в 128 бит. В PGP нетрадиционно построена система управления криптографическими ключами пользователей. В разветвленных корпоративных сетях типа сети Интернет сложной проблемой является исключение навязывания ложной ключевой информации при взаимном обмене пользователями своими открытыми ключами.
Слайд 8Классические протоколы распределения ключей предписывают предварительно рассылать сформированные самими пользователями или центром
Классические протоколы распределения ключей предписывают предварительно рассылать сформированные самими пользователями или центром

Слайд 9Поэтому подлинность полученных по каналу связи открытых ключей нового корреспондента подтверждает цифровая
Поэтому подлинность полученных по каналу связи открытых ключей нового корреспондента подтверждает цифровая

Для повышения подлинности передаваемых открытых ключей в PGP рекомендуется заверять их подписями нескольких корреспондентов сети, честность которых не подвергается сомнению получателями ключевой информации. При такой схеме первоначально требуется заверить свои ключи подписью доверенных лиц, выполняющих функции нотариусов, и затем доверие к открытым ключам корреспондентов-нотариусов будет распространяться на заверенные ключи. В программе PGP для шифрования передаваемых сообщений может использоваться симметричный алгоритм IDEA и несимметричный алгоритм шифрования RSA.
Слайд 10Достоинством первого является более высокая скорость работы (практически на два порядка быстрее
Достоинством первого является более высокая скорость работы (практически на два порядка быстрее

Слайд 11Одним из основных достоинств PGP является удобство управления ключами.
Программа PGP сама
Одним из основных достоинств PGP является удобство управления ключами.
Программа PGP сама

Несанкционированный доступ к связкам ключей, записанных на магнитных носителях, предотвращается с помощью известного только законному пользователю пароля.
Слайд 12Для удобства пользования большим количеством ключей каждому ключу –связке поставлен в соответствие
Для удобства пользования большим количеством ключей каждому ключу –связке поставлен в соответствие

Слайд 13Однонаправленная функция с потайным ходом на основе алгебраических уравнений по модулю 2
Для
Однонаправленная функция с потайным ходом на основе алгебраических уравнений по модулю 2
Для

Известна теорема о том, что решение алгебраических уравнений по модулю 2 в общем случае является NP сложных задач. Применим эту теорему для построения ОНФ пх следующего вида:
Пусть вектор сообщения состоит из двух частей длиной по n бит каждая М=(М0, М1), где М0, М1 есть левая и правая части вектора сообщения соответственно; вектор ключа К определим, как совокупнось подвектора К={K1, K2,…, Kd-1}, каждый подвектор Ki, i=1,…,d-1 включает n бит из вектора ключа К. Ki=(ki1,ki2,…,kin), где kijЄ K, j=1, 2,…,n.
Над вектором М d раз циклически выполним операции вида
Мi=Mi-2 + f (Ki-1, Mi-1), 2≤i≤d, где f есть некоторое фиксированное нелинейное преобразование, и все действия выполняются по mod 2.
Значение ОНФ f от аргументов М и К равно С=f (M, K)=(Md-1, Md)
Слайд 14Для законного получателя, знающего К, ОНФ обратима. Получатель рекурсивно восстанавливает входной вектор
Для законного получателя, знающего К, ОНФ обратима. Получатель рекурсивно восстанавливает входной вектор

Мd-2= Мd + f(Kd-1, Md-1)
Мd-3= Мd-1 + f(Kd-2, Md-2) до получения сообщения М=(М0, М1).
Для данной ОНФ с пх обращение функции при знании ключа К (К - параметр потайного хода) является вычислительно простой задачей, как и прямая задача. Для необратимости данной функции при неизвестном ключе необходимо, чтобы преобразование f влялось нелинейным преобразованием вида: f (ki1,ki2,…,kim; mi1,mi2,…,min=(p1, p2,…,pn) и могло быть описано совокупностью полиномов р от тех же аргументов.
Можно показать, что при известных значениях сообщения М и криптограммы С вычисление вектора ключа К (атака со знанием открытого сообщения) сводится к решению системы алгебраических уравнений с неизвестными К1, К2,…,Кd-1
Слайд 15Это-NPсложная задача. Пример. Пусть n=3,
f (Ki, Mi)=f(ki1, ki2, ki3; mi1, mi2,
Это-NPсложная задача. Пример. Пусть n=3,
f (Ki, Mi)=f(ki1, ki2, ki3; mi1, mi2,

=(ki1ki2mi1mi2, ki2ki3mi1mi3, (ki1+ki2)mi1mi3)
Пусть вектор ключа К состоит из 8 бит вида К=(к1,к2,…,к8)
и сформируем совокупность подвекторов ключа по правилу:
К1=(к2,к4,к6), К2=(к1,к2,к7), К3=(к3,к5,к8), К4=(к6,к7,к8)
Пусть вектор сообщения М=(101111), из него получим левую и правую части М0=(101) и М1=(111).
Выполним ОН преобразования вида М2 = М0+f (K1,M1)=
=(101)+(k2k4,k4k6,k2+k4)=(1+ k2k4,k4k6,1+k2+k4), M3=M1+f(k1,k2,k7,M2) и т.д. Выполнив две итерации данной ОНФ получим криптограмму длиной 2n бит С=(М2,М3). Данная функция вычисляется в прямом направлении и обращается при знании ключа, но при нелинейной f и неизвестном ключе, ее обращение вычислительно сложно. Рассмотренный принцип построения ОНФ с пх используется при построении блочных систем шифрования (класс блочных шифров Фейстеля), к которому принадлежит DES и согласно ГОСТ 28147-89.
Слайд 16К настоящему времени предложено большое количество ОНФ с пх, построенных на основе
К настоящему времени предложено большое количество ОНФ с пх, построенных на основе

-отыскание дискретного логарифма элемента в большом конечном поле или группе (криптосистема открытого распространения ключей Диффи-Хэллмана, цифровая подпись Эль-Гамаля, криптосистема цифровой подписи сообщений Шнорра и др.)
-разложение больших чисел на простые множители (цифровая подпись сообщений РША, цифровая подпись Рабина и др.
-задача об укладке целочисленного ранца( класс ранцевых систем шифрования информации Меркля-Хэллмана)
-декодирование неизвестных получателю кодов Гоппы (класс систем шифрования информации Мак-Эллиса)
Слайд 17КРИПТОГРАФИЧЕСКИЕ ХЭШ-ФУНКЦИИ
Криптографические хэш-функции (КХФ) в настоящее время широко используются для решения
КРИПТОГРАФИЧЕСКИЕ ХЭШ-ФУНКЦИИ
Криптографические хэш-функции (КХФ) в настоящее время широко используются для решения

Область применения постоянно увеличивается. Уникальные свойства криптографических хэш-функций позволяют использовать их для формирования шифрующих последовательностей в шифрообразуюших устройствах, для обеспечения секретности непрерывных и дискретных сообщений, для формирования случайных чисел в криптогра-фических системах и во многих других приложениях. Понятие "криптографические хзш-функции" было определено в 1979 году в работах американского математика Р. Меркля. однако еще ранее в автоматизированных системах широко использовались некриптографические хэш-функции для оптимизации размещения и поиска данных.
Слайд 18 Хэш-функции (ХФ) произвольного вида принадлежат классу однонаправленных функций без потайного хода.
Хэш-функции (ХФ) произвольного вида принадлежат классу однонаправленных функций без потайного хода.

Определение: в общем случае хэш-функцией является произвольная функция h, которая имеет, как минимум, два свойства:
– сжатие: функция h отображает входную дискретную последовательность произвольного конечного размера в выходную последовательность фиксированной длины n;
– вычислительная простота определения значения хэш-функции: для заданной функции h и входной последователь-ности X легко вычислить значение h(X). Вычислительная простота означает, что для вычисления значения хэш-функции требуется полиномиалъное число операций относительно размерности входной последовательности.
Слайд 19 Идея хэширования сообщений заключается в следующем.
Пусть множество информационных сообщений {X}
Идея хэширования сообщений заключается в следующем.
Пусть множество информационных сообщений {X}

Н = h(Х).
Если различные сообщения X ≠X1 отображаются в один и тот же хэш-код , h(X)=h(X1)
то данная хэш-функция допускает коллизии (склеивания) сообщений. Количество коллизий для каждого хэш-кода обозначим ti, где i = 1,2, ... ,N, а N- общее число различных хэш-кодов. Очевидно, что число различных хэш-кодов не превышает величины 2n , где n – двоичная длина хэш-кодов. Одной из важнейших характеристик хэш-функции является индекс хэширования (склеивания) I (h,S) функции h на словаре S:
Слайд 20Если I(h,S)=0, то коллизий не происходит, каждое сообщение хэшируется в свой, отличный
Если I(h,S)=0, то коллизий не происходит, каждое сообщение хэшируется в свой, отличный

Хэш-функции, обеспечивающие I(h,S)=0 , называются совершенными хэш-функциями. Однако построить совершенную хэш-функцию для достаточно большого словаря весьма сложно. Поэтому на практике обычно используют хэш-функции, индекс склеивания которых, хотя и не равен нулю, но достаточно к нему близок.
Использование некриптографических хэш-функций, например, в базах данных позволяет существенно уменьшить емкость запоминающих устройств для размещения записей (сообщений) и ускорить доступ к ним. Адресом для размещения записей служит значение кэш-кода h(X), вычисленное из двоичного представления записи X. Если коллизии происходят, то для их разрешения используются дополнительные механизмы, например повторное хэширование сообщений.
Слайд 21Хэширующие функции обычно ведут себя как случайные функции: распределение хэш-кодов равновероятно и
Хэширующие функции обычно ведут себя как случайные функции: распределение хэш-кодов равновероятно и

Криптографические хэш-функции, являясь подклассом хэш-функпий, должны обладать дополнительными свойствами, выполняемыми при условии, что нарушитель знает описание функции и статистические характеристики множества сообщений и множества хэш-кодов:
– стойкость к вычислению прообраза – для почти всех значений хэш-функции вычислительно невозможно отыскать любой прообраз, который хэшируется к заданному значению; – стойкость к вычислению второго прообраза – вычислительно невозможно (отыскать любой второй прообраз, который
Слайд 22хэшируется в такое же значение хэш-функции, как любой заданный прообраз, то есть
хэшируется в такое же значение хэш-функции, как любой заданный прообраз, то есть

– стойкость к образованию коллизий – вычислительно
невозможно отыскать любые два различных прообраза X и X', которые хэшируются в одинаковое значение хэш-функции, то есть выполняется h(X)=h(X1).
Первое свойство характеризует криптографические хэш-функции как однонаправленные функции: нарушитель не в состоянии вычислить сообщение X по его известному хзш-коду . Второе и третье свойства принципиально различаются тем. что стойкость к вычислению второго прообраза должна обеспечиваться в условиях, когда первый прообраз фиксирован для нарушителя, а стойкость к коллизиям предполагает, что он волен выбирать любые прообразы.
, не равный X, такой, что
Слайд 23классификация КХФ
классификация КХФ
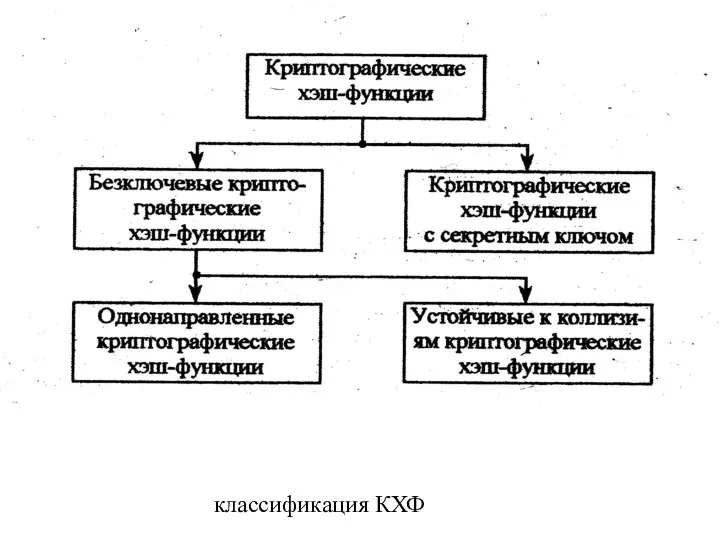
Слайд 24 Если в процессе хэширования сообщений используется секретный ключ К, то такая
Если в процессе хэширования сообщений используется секретный ключ К, то такая

Бесключевые криптографические хэш-функции
Определение 11: Бесключевая криптографическая хэш-функция называется однонаправленной криптографической хэш-функцией (ОНХФ), если она является стойкой к вычислению прообраза и стойкой к вычислению второго прообраза
Определение 12: Бесключевая криптографическая хэш-функция называется устойчивой к коллизиям криптографической хэш-функцией (УКХФ), если она является
Слайд 25стойкой к образованию коллизий и стойкой к вычислению
второго прообраза.
Иногда используются альтернативные
стойкой к образованию коллизий и стойкой к вычислению
второго прообраза.
Иногда используются альтернативные

Бесключевые КХФ ориентированы на обеспечение подлинности и целостности информации и предназначены для построения цифровой подписи сообщений, аутентификации пользователей и корреспондентов систем и сетей. Используются в симметричных и несимметричных системах защиты информации. Например, в несимметричных системах для исключения возможности подделки нарушителем сообщений заверяемое сообщение сначала хэшируется по БКХФ, а затем его хэш-код подписывается с использованием секретного ключа формирования ЦП сообщений.
Выбор функции зависит от условий применения и возможностей нарушителя. Если он при атаке способен выбирать сообщения для подделки, то необходимо использовать УКХФ.
Слайд 26Если нет – то можно использовать ОКХФ.
Стойкость ОНКХФ к вычислению прообраза может
Если нет – то можно использовать ОКХФ.
Стойкость ОНКХФ к вычислению прообраза может

Максимально достижимая стойкость УКХФ к вычислению второго прообраза - О(2n) операций хэширования, а стойкость к коллизиям - О(2n/2) операций хэширования. Пояснить верхнюю границу стойкости можно на основе известного в математике «парадокса дня рождения». Подсчитано, что в случайно выбранной группе из 24 человек вероятность наличия хотя бы двух людей с одинаковым днем рождения
Слайд 27составляет не менее 0.5. Атака нарушителя на хэш-функцию с использованием «парадокса» может
составляет не менее 0.5. Атака нарушителя на хэш-функцию с использованием «парадокса» может

Вероятность того, что хэш-код хотя бы одного ложного сообщения совпадет с хэш-кодом истинного равна: Р=1-2 (r1r2/2n)
Для значений r1и r2 порядка 2n/2. Это означает, что, перебрав r1=r2=2n/2 хэш-кодов, нарушитель с вероятностю 0.5 отыщет хотя бы одно ложное и коллизирующее с ним истинное, подмену которого обнаружить невозможно. В настоящее время для обеспечения вычислительной стойкости УКХФ требуется выбор n не менее 128 бит. Стойкость УКХФ выше, чем ОКНХФ. Большинство БКХФ основано на разбиении длинного сообщения на блоки фиксированной длины и их последовательной обработке КХФ одним и тем же образом.
Слайд 28Этот метод называется итеративным хэшированием. Сообщение Х делится на t блоков X1,X2,…,Xt
Этот метод называется итеративным хэшированием. Сообщение Х делится на t блоков X1,X2,…,Xt

Если длина сообщения не кратна длине блока b, она дополняется до кратной длины. Для инициализации итеративного хэширования необходимо задать: стартовый вектор хэширования Н0 длиной n бит. Хэширование может быть последовательно описано действиями:
Х=(Х1,….,Хi, …,Xt), i=1, 2, …t
H=f (Xi, Hi-1), i=1, 2, …t
h(X)=Ht, где Нi – значение хэш-кода функции на i-той итерации хэширования, f t, где Нi – значение хэш-кода функции на i-той итерации хэширования, f отображает n битовое предыдущее состояние хэш-кода Нi-1 и b-битовый блок сообщения Хi в очередное nбитовое значение хэш-кода Нi, а значение хэш-кода и h(X) всего сообщения Х определяется как значение хэш-кода на последней итерации хэширования.
Слайд 29Функция f называется шаговой функцией хэширования (иначе – круговая). Для обеспечения стойкости
Функция f называется шаговой функцией хэширования (иначе – круговая). Для обеспечения стойкости

Правило выбора стартового вектора должно исключать возможность вычислительно простого формирования коллизий.
Исследования стойкости сосредоточены на вопросе: каким условиям должна удовлетворять функция f, чтобы обеспечить стойкость. Получены два результата: 1- необходимые и достаточные условия для f ,обеспечивающей максимально достижимую стойкость ОНКХФ.
Теорема 1.Пусть дополнение включено в хэшируемое сообщение, сообщение без дополнения содержит по крайней мере 2 блока. Тогда обнаружение второго прообраза для h с фиксированным стартовым вектором хэширования требует 2n вычислительных операций, если и только если для нахождения второго прообраза для шаговой функции f с произвольным выбором Нi-1 требуется 2n выч.операций
Слайд 30Т.е. если f м.б. инвертирована менее, чем за 2n операций, то для
Т.е. если f м.б. инвертирована менее, чем за 2n операций, то для

Теорема 2. Пусть дополнение однозначно и включено в хэшируемое сообщение. Если шаговая функция f устойчива к образованию коллизий, то функция h есть устойчивая к коллизиям КХФ. Обе теоремы говорят о важности выбора шаговой функции f.
Принципы построения бесключевых криптографических хэш-функций. Практически итеративные БКХФ делятся на два класса: функции, основанные на блочных алгоритмах и специально разработанные.
На основе блочных алгоритмов шифрования используется метод Уинтерница: сообщение М разбивается на блоки, по длине равные длине ключа, и на этих блоках, как на ключах, последовательно шифруется фиксированный стартовый вектор хэширования. Т.к. алгоритмы шифрования должны обеспечить стойкость к криптоанализу при атаке нарушителя, автоматически обеспечивается выч. невозможность определения прообраза по известному нарушителю хэш-коду.
Слайд 31Вычисление криптографической хэш-функции методом Уинтерница
Использование операции блочного хэширования Е –это вычисление криптограммы
Вычисление криптографической хэш-функции методом Уинтерница
Использование операции блочного хэширования Е –это вычисление криптограммы
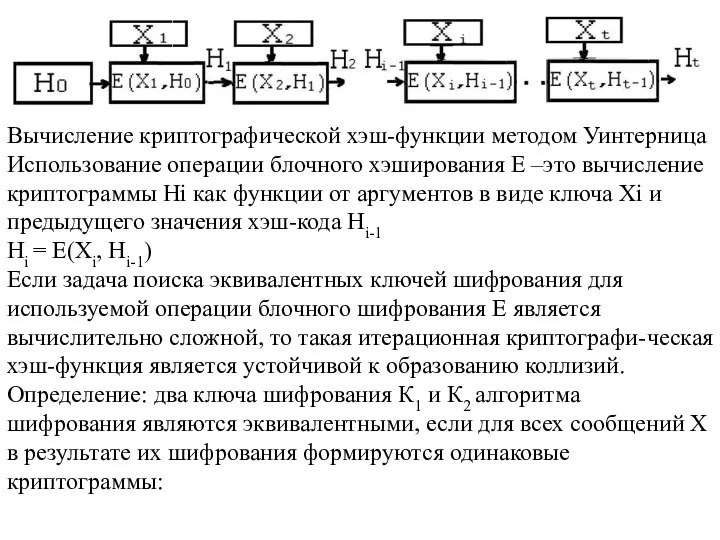
Hi = E(Xi, Hi-1)
Если задача поиска эквивалентных ключей шифрования для используемой операции блочного шифрования Е является вычислительно сложной, то такая итерационная криптографи-ческая хэш-функция является устойчивой к образованию коллизий. Определение: два ключа шифрования К1 и К2 алгоритма шифрования являются эквивалентными, если для всех сообщений Х в результате их шифрования формируются одинаковые криптограммы:
Слайд 32Е(Х, К1) = Е(Х, К2)
Поэтому большинство известных КХФ построено на основе алгоритмов
Е(Х, К1) = Е(Х, К2)
Поэтому большинство известных КХФ построено на основе алгоритмов

Отдельный класс – специально разработанные хэш-функции.
К этому классу принадлежит УКХФ, называемая SHA (Security hesh algorithm), принципы построения и использования которой определены национальным стандартом США FIPS. Она предназначена для обеспечения защиты от подделки сообщений, заверяемых в криптосистеме цифровой подписи сообщений DSS в соответствии с национальным стандартом. Эта функция выполняет необратимое сжатие заверяемого сообщения многократным применением ОНФ спец.вида.
Длина хэш-кода SHA – 160 бит, поэтому достижимая оценка её стойкости к образованию коллизий составляет 2n/2 =2 80 операций, что считается достаточным.
В международных сетях используются УКХФ MD4 и MD5, разработанные криптографом Р.Райвестом.
Слайд 33Также известны ОН и УКХФ, основанные на высокой вычислительной сложности задачи факторизации
Также известны ОН и УКХФ, основанные на высокой вычислительной сложности задачи факторизации

Принципы построения УКХФ согласно ГОСТ Р34.11-94
Реализован в государственном стандарте России «Информационная технология Криптографическая защита информации.Функция хэширования».
Правило формирования. Хэшируемое сообщение разделяется на последовательные информационные блоки длиной по 256 бит.
Слайд 34Если последний блок неполный, то слева к нему дописываются нулевые символы до
Если последний блок неполный, то слева к нему дописываются нулевые символы до

Каждый блок h шифруется в режиме простой замены согласно алгоритму по ГОСТ на Кi ключе шифрования. Конкатенация полученных таким образом четырех криптограмм длиной по 64 образует шифрованную последовательность длиной 256 бит:
Si=s4||s3||s2||s1
Слайд 35На третьем этапе выполняется перемешивающее преобразование Ψ шифрованной последовательности Si с учетом
На третьем этапе выполняется перемешивающее преобразование Ψ шифрованной последовательности Si с учетом

Hi = Ψ61 (Hi-1 + Ψ(Xi Ψ12(Si))), где Ψj означает j число итераций перемешивающего преобразования. Полученная величина Нi является значением хэш-кода очередного информационного блока Хi. Итеративно обрабатывая последовательно поступающие информационные блоки пошаговой функции хэширования f формируется хэш-код всего сообщения. Хэширование последнего блока выполняется в зависимости от значений контрольной суммы и длины всего сообщения, что обеспечивает повышение стойкости данной хэш-функции к образованию коллизий и защищает от атаки нарушителя, при которой он пытается создать ложное сообщение из истинного.
Максимально достижимая оценка стойкости может составлять порядка 2n/2=2128 вычислительных операций.
Слайд 36Криптографические хэш-функции с секретным ключом.
Определение 14: хэш-функция называется КХФ с секретным ключом,
Криптографические хэш-функции с секретным ключом.
Определение 14: хэш-функция называется КХФ с секретным ключом,

простота вычисления при знании ключа: Н = h (X, K) вычислительно просто определяется для любого сообщения Х и любого допустимого значения ключа К,
сжатие для произвольно длинного сообщения Х функция формирует хэш-код Н фиксированной длины n,
- вычислительная устойчивость: для произвольного значения Хi вычислительно невозможно определение значения его хэш-кода Нi без знания ключа Кi даже при известном произвольно большом количестве пар {Xi, h(Xi, K)}, где Хi≠Xj,
- вычислительная необратимость относительно ключа: невозможно определние ключа К даже при известном произвольно большом количестве пар {Xi, h(Xi,K)} вычислительно невозможно.
Криптографические хэш-функции с секретным ключом часто называют кодами аутентификации сообщений (КАС), т.к. первой областью их применения являлась аутентификация.
Слайд 37КХФ с секретным ключом делятся на два класса: основанные на блочных алгоритмах
КХФ с секретным ключом делятся на два класса: основанные на блочных алгоритмах

Как и БКХФ КХФ с ск строятся как итеративные, использующие шаговые функции хэширования. На основе СКХФ формируется имитовставка в отечественном стандарте шифрования данных ГОСТ РФ28147-89 «Системы обработки информации.Защита криптографическая. Алгоритм криптографического преобразования.».
Принципы построения. Хэшируемое сообщение Х делится на t блоков от Xi до Xt длиной b=64 бита. Если длина сообщения не кратна длине блока, то сообщение должно дополняться до длины, кратной длине блока. Для инициализации процесса итеративного хэширования задается нулевой стартовый вектор хэширования H0 длиной 64 бита. Хэширование сообщения Х м.б.описана следующими действиями:
Х=(X1,…,Хi,…,Xt), i=1,2,…t
Hi=f (Xi,+Hi-1,K) , i=1, 2,…t, где Hi –значение хэш-кода функции на i-той итерации хэширования, функция f отображает n-битовое предыдущее значение хэш-кода Hi-1 и b-битовый блок сообщения
Слайд 38Хi в очередное n-битовое значение хэш-кода Hi, а значение хэш-кода h(X, K)
Хi в очередное n-битовое значение хэш-кода Hi, а значение хэш-кода h(X, K)

Особенностью рассматриваемой СКХФ является обязательное шифрование хэшированных сообщений. Это повышает стойкость данной хэш-функции к поиску и нарушителем коллизий и стойкость к формированию второго прообраза и оправдывает сравнительно малую длину формируемого по ГОСТ хэш-кода 16…32 бита. Это принципы построения СКХФ на основе блочных шифров в режиме сцепления блоков шифра. Такие функции формируют коды длиной 128 бит, что позволяет отказаться от обязательного шифрования самого сообщения. Стойкость их повышается при использовании вместо обратимых шаговых функций шифрования функций, не имеющих обратного преобразования. Кроме того, известны СКХФ на основе блочных шифраторов в режиме обратной связи по шифру: X=(X1,…,Xi,…,Xt), i=1,2,…,t
Hi=f(Hi-1,K)+X, для i=1,2,…,t; h (X,K)=Ht
 Сетевой уровень (Network)
Сетевой уровень (Network) Защита ребенка в виртуальном мире
Защита ребенка в виртуальном мире Антивирусные программы
Антивирусные программы Защита web-сайта Моё электронное портфолио
Защита web-сайта Моё электронное портфолио Источники информации. Тест (2 класс)
Источники информации. Тест (2 класс) Макрос DragAndDrop
Макрос DragAndDrop Суперкомпьютер IBM Roadrunner
Суперкомпьютер IBM Roadrunner Марк Цукерберг
Марк Цукерберг Сравнительная характеристика автоматизированных библиотечно-информационных систем
Сравнительная характеристика автоматизированных библиотечно-информационных систем Лаборатория онлайн бизнеса 2021
Лаборатория онлайн бизнеса 2021 Знаковые информационные модели
Знаковые информационные модели База данных (БД)
База данных (БД) Базы данных-3
Базы данных-3 Презентация на тему Информация и цивилизация
Презентация на тему Информация и цивилизация  Восхождение на гору Информация
Восхождение на гору Информация Физические принципы формирования ячейки памяти постоянного запоминающего устройства
Физические принципы формирования ячейки памяти постоянного запоминающего устройства Информационные технологии. Лекция 1
Информационные технологии. Лекция 1 Презентація
Презентація Использование информационных сервисов Учебная работа в группах и Мастер рефератов
Использование информационных сервисов Учебная работа в группах и Мастер рефератов Знакомство с NRG food. Первый ознакомительный лэнд
Знакомство с NRG food. Первый ознакомительный лэнд Репозиторий. Проблемы и перспективы
Репозиторий. Проблемы и перспективы 01_Введение в архитектуру вычислительных систем (02.03.02 ФИИТ, презентация)
01_Введение в архитектуру вычислительных систем (02.03.02 ФИИТ, презентация) Briefing designers
Briefing designers Алгоритм получения доступа к Электронному дневнику
Алгоритм получения доступа к Электронному дневнику Презентация на тему Виды и классификация моделей
Презентация на тему Виды и классификация моделей  Проектирование информационных систем
Проектирование информационных систем Поиск записей в табличной базе данных с помощью фильтров
Поиск записей в табличной базе данных с помощью фильтров Устройства компьютера
Устройства компьютера