Логические основы вычислительной техники

Англичанин Джордж Буль (1815-1864, математик-самоучка), на фундаменте, заложенном Лейбницем, создал новую область науки - Математическую логику (Булеву алгебру или Алгебру высказываний). В его работах логика обрела свой алфавит, свою орфографию и грамматику.
Немецкий ученый Готфрид Лейбниц (1646-1716) заложил основы математической логики. Он пытался построить первые логические исчисления (свести логику к математике), предложил использовать символы вместо слов обычного языка, поставил много задач по созданию символьной логики, его идеи оказали влияние на последующие работы ученых в этой области.
Математическая логика

Алгебра логики (высказываний) работает с высказываниями.
Различают:
Логические константы (логические утверждения) – конкретные частные утверждения
{Аристотель - основоположник логики}
{На яблонях растут бананы}
2. Логические переменные (предикаты) – логические высказывания, значения которых меняются в зависимости от входящих в них переменных, обозначаются заглавными латинскими буквами А, В, С, D, F,…
А = {Аристотель - основоположник логики}
В = {На яблонях растут бананы}.
Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом, А = 1, В = 0.

3. Логические функции ( логические формулы) – сложные логические выражения образованных из простых и связанных логическими операциямим И, ИЛИ, НЕ и др.)
Высказывание “Все мышки и кошки с хвостами”
является сложным и состоит из двух простых высказываний.
А=“Все мышки с хвостами” и В=“Все кошки с хвостами”
Его можно записать в виде логической функции, значение которой истинно: F(A,B)=A и B
В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть только ложно (0) или истинно (1).

Логические операции
Отрицание (инверсия).
Обозначение: НЕ А, ¬А,
А={Дети любят игрушки} = {Дети НЕ любят игрушки}

2. Логическое умножение (Конъюнкция) Обозначение: И, ∧, &, •
А={Множество обитателей моря}
В={Множество млекопитающих}
F=A ^ B= {кит, акула, дельфин}
Таблица истинности:
F= А ∧ В

3. Логическое сложение (Дизъюнкция)
Обозначение: ИЛИ,∨, +, |
F=A V B= {Множество учеников 10А или 10Б кл.}
Таблица истинности:
F= А ∨ В

4. ИМПЛИКАЦИЯ (логическое следование)
условие
следствие
ЕСЛИ, ...
ТО ...
=>
условие
следствие
Если будет дождь, то мы не пойдем на улицу.
Если я поленюсь, то получу двойку.
Если на траве роса, то скоро настанет вечер.
Обозначение: А→В, А⇒В
Таблица истинности:
Импликация - логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

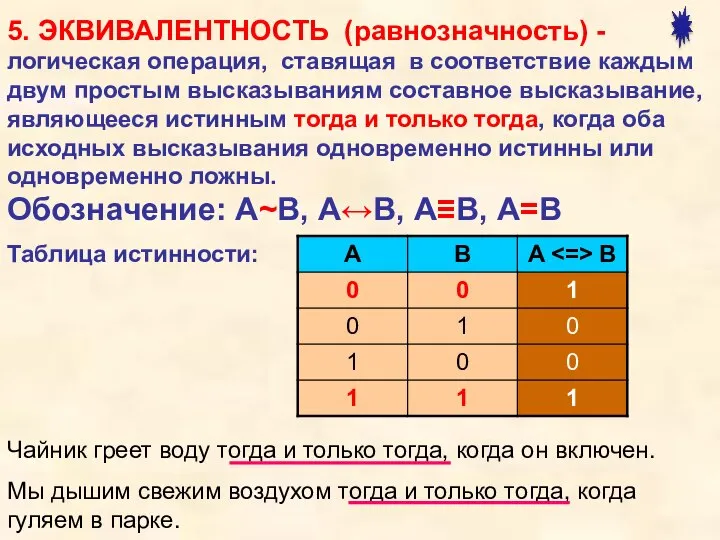
5. ЭКВИВАЛЕНТНОСТЬ (равнозначность) -
Чайник греет воду тогда и только тогда, когда он включен.
Мы дышим свежим воздухом тогда и только тогда, когда гуляем в парке.
Обозначение: А~В, А↔В, А≡В, А=В
логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
Таблица истинности:

РЕШИМ ЗАДАЧИ:
Приоритет логических операций:
() Операции в скобках
НЕ Отрицание
И логическое умножение
ИЛИ Логическое сложение
→ Импликация
↔ Эквивалентность

Вычисление логических выражений
Пример1.
Вычислить значение логического выражения
«(2·2=5 или 2·2=4}) и (2·2 ≠ 5 или 2·2 ≠ 4)»
Обозначим
А=«2·2=5» – ложно (0)
В=«2·2=4» – истинно (1)
Тогда (А или В) и ( или )

Задание 2. Определите истинность составного высказывания
состоящего из простых высказываний:
А={Принтер – устройство вывода информации}
В={Процессор – устройство хранения информации}
C={Монитор – устройство вывода информации}
D={Клавиатура – устройство обработки информации}
Определяем истинность составного высказывания:
А=1, В=0, С=1, D=0
Установим истинность простых высказываний: