Содержание
- 2. В итерационных циклах производится проверка некоторого условия, и в зависимости от результата этой проверки происходит либо
- 3. Цикл с постусловием Оператор повтора repeat состоит из заголовка (repeat), тела условия окончания (until). repeat Инструкции
- 4. Описание работы Цикл работает так: вначале выполняется тело цикла — инструкции, которые находятся между repeat и
- 5. Цикл repeat — это цикл с постусловием, т. е. инструкции тела цикла будут выполнены хотя бы
- 6. Цикл repeat удобно использовать для обработки ошибки ввода при несоответствии типа введенных данных типу переменной. В
- 7. var х: integer; ok: boolean; begin repeat writeln('Введите целое x'); {$i-} {отмена стандартного контроля оп-й ввода/вывода
- 8. Цикл с предусловием while Условие_выполнения_цикла do begin Инструкции end; Условие выполнения цикла — это выражение логического
- 9. Описание работы Цикл while работает так: вначале выполняется проверка значения Условие выполнения цикла — если значение
- 10. Пример. Найти НОД двух натуральных чисел, используя алгоритм Евклида. var a, b:integer; begin writeln(‘Введите два натуральных
- 11. Пример. Пользователь вводит целое положительное число. Определите, какое минимальное количество последовательно расположенных натуральных чисел необходимо сложить,
- 12. Численные методы решения алгебраических и трансцендентных уравнений Дано нелинейное уравнение: f(x)=0. Если функцию можно привести к
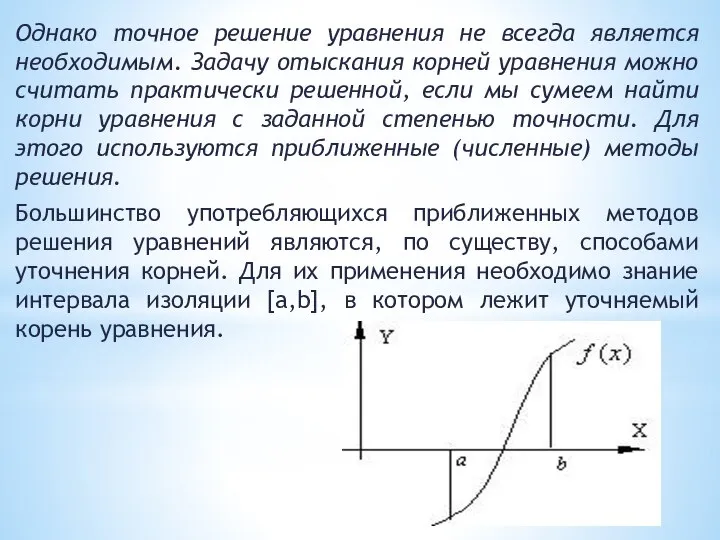
- 13. Однако точное решение уравнения не всегда является необходимым. Задачу отыскания корней уравнения можно считать практически решенной,
- 14. Процесс определения интервала изоляции [a,b], содержащего только один из корней уравнения, называется отделением этого корня. Процедура
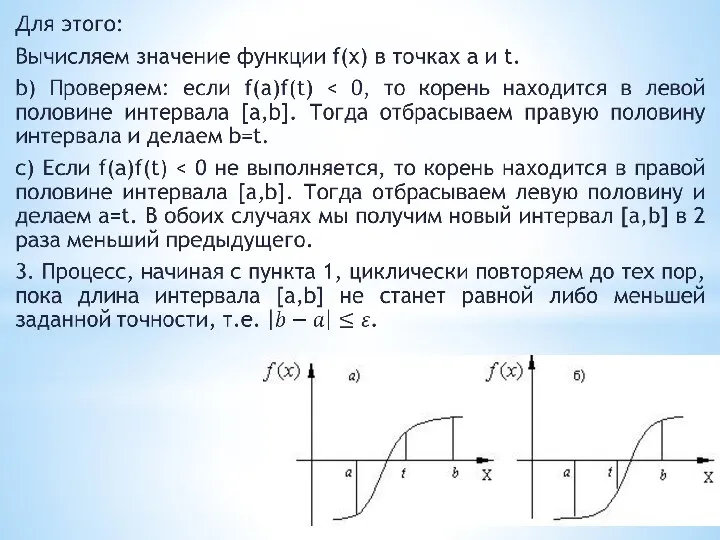
- 15. Метод половинного деления
- 17. Const e=0.001; Var x, t, a, b:real; function f1(x:real):real; begin f1:=sin(x); end; begin writeln(‘Введите a, b’);
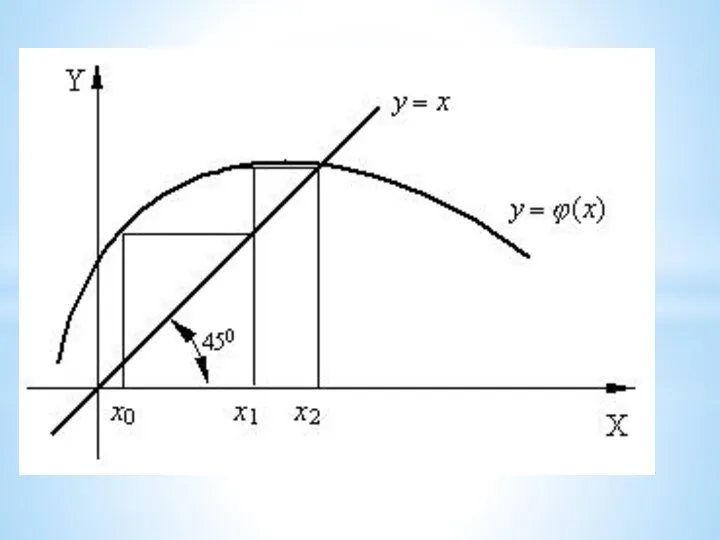
- 18. Метод простых итераций
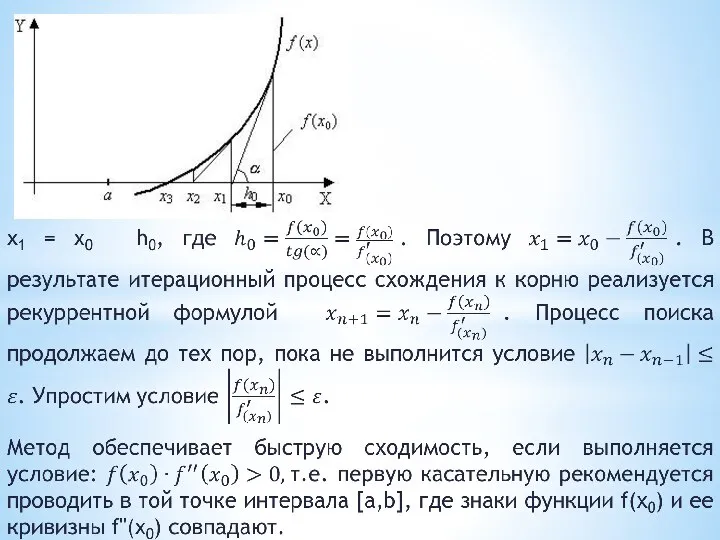
- 20. Метод Ньютона (метод касательных) Метод Ньютона относится к градиентным методам, в которых для нахождения корня используется
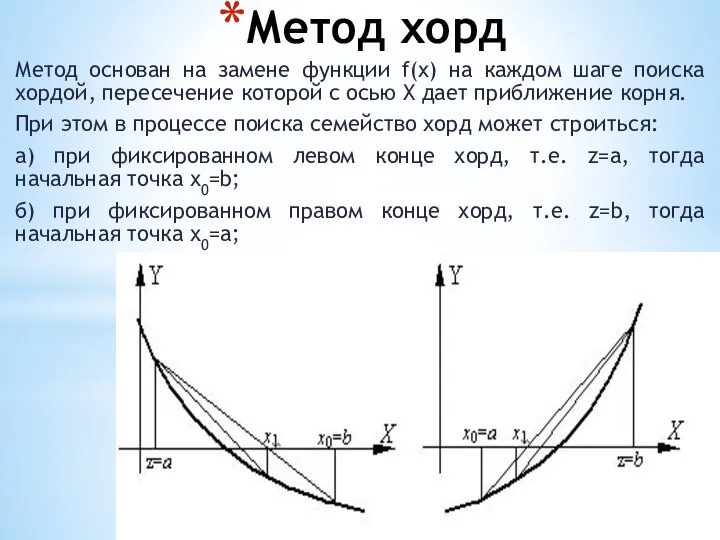
- 22. Метод хорд Метод основан на замене функции f(x) на каждом шаге поиска хордой, пересечение которой с
- 25. Скачать презентацию











![Процесс определения интервала изоляции [a,b], содержащего только один из корней уравнения, называется](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/931758/slide-13.jpg)





 1С- Битрикс. Структура bitrix framework, работа с административной панелью, редактирование меню
1С- Битрикс. Структура bitrix framework, работа с административной панелью, редактирование меню 50 главных категорий контента
50 главных категорий контента Системы счисления. Математические основы информатики
Системы счисления. Математические основы информатики Каналы Связи
Каналы Связи Оценка сайтов
Оценка сайтов Передача данных. МПСвЭПиТК
Передача данных. МПСвЭПиТК Ячейки памяти компьютера
Ячейки памяти компьютера Понятие концепции наследования. Видимость компонентов
Понятие концепции наследования. Видимость компонентов Online-курсы Платформа Открытое образование
Online-курсы Платформа Открытое образование Индивидуальный проект. От абака до компьютера
Индивидуальный проект. От абака до компьютера Правила пользования компьютерной сетью ООО Гутцайт групп
Правила пользования компьютерной сетью ООО Гутцайт групп Аксиомы и определения доступа субъектов к объектам
Аксиомы и определения доступа субъектов к объектам Алгоритмизация и программирование
Алгоритмизация и программирование Кафедра информационной и технологической культуры
Кафедра информационной и технологической культуры Как с помощью продукции повседневного ухода за собой получить доход в интернете
Как с помощью продукции повседневного ухода за собой получить доход в интернете Поштові служби інтернету. Електронна скринька та електронне листування
Поштові служби інтернету. Електронна скринька та електронне листування Текстовая информация. Единицы измерения
Текстовая информация. Единицы измерения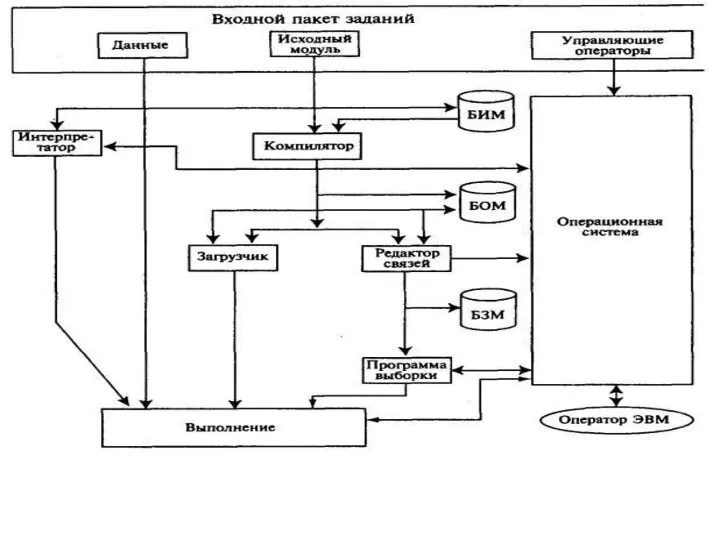 Входной пакет заданий
Входной пакет заданий Архитектура персонального компьютера
Архитектура персонального компьютера История интернета
История интернета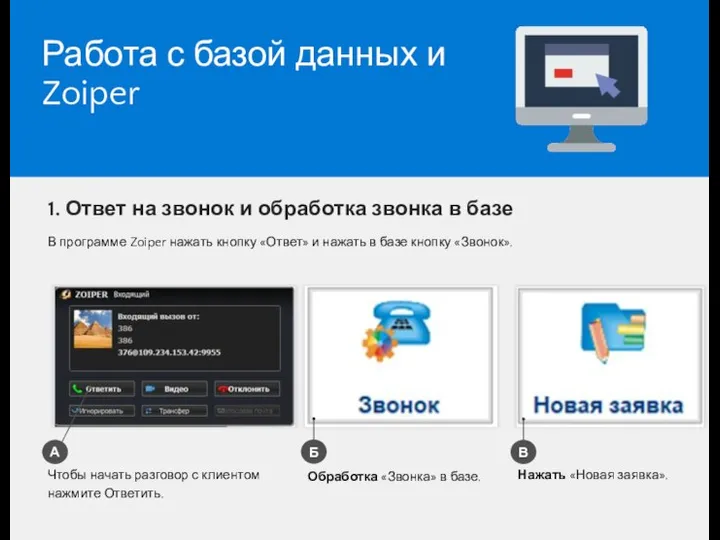 Работа с базой данных и Zoiper
Работа с базой данных и Zoiper Темная сторона цифрового мира. О массовой уязвимости процессоров Intel
Темная сторона цифрового мира. О массовой уязвимости процессоров Intel Основы программирования на языке Python. Школа::Кода (занятие 3)
Основы программирования на языке Python. Школа::Кода (занятие 3) Информация и ее свойства
Информация и ее свойства Проектирование структуры БД. Методические указания к курсовой работе Разработка и эксплуатация АИС Часть 1
Проектирование структуры БД. Методические указания к курсовой работе Разработка и эксплуатация АИС Часть 1 Программирование на языке C++
Программирование на языке C++ Компьютерные сети
Компьютерные сети Крестики-нолики. Шаблон
Крестики-нолики. Шаблон