Изменения в единицах измерения

2
Мы продемонстрируем это для оценок коэффициентов регрессии. Начнем с предположения, что истинная и расчетная модели приведены выше.
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ

3
Предположим теперь, что единицы измерения Y изменяются, причем новая мераY*, является линейной функцией старой.
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ

4
Как правило, изменение единицы измерения включает в себя простое мультипликативное масштабирование, например, когда мы конвертируем фунты в граммы.
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ

5
Иногда происходит линейное преобразование. Примером может служить конверсия температур от градусов Цельсия до градусов Фаренгейта.
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ

6
Показан новый коэффициент наклона b2*.
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ

7
Подставим Y*.
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ

8
Остается только λ2.
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ

9
Мы находим, что новый коэффициент наклона равен исходному, умноженному на λ2.
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ

10
Это логично. Единичное изменение в Y такое же, как изменение λ2 единиц в Y*. Согласно уравнению регрессии, единичное изменение X приводит к изменению b2 единиц вY, поэтому это должно привести к изменению λ2b2 единиц вY*.
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ

11
Эффект изменения единиц измерения X оставлен в качестве упражнения.
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ

12
Мы рассмотрим частный случай изменения единиц измерения X. Часто свободный член в уравнении регрессии не имеет разумной интерпретации, потому что X = 0 расположен далеко от диапазона данных.
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ

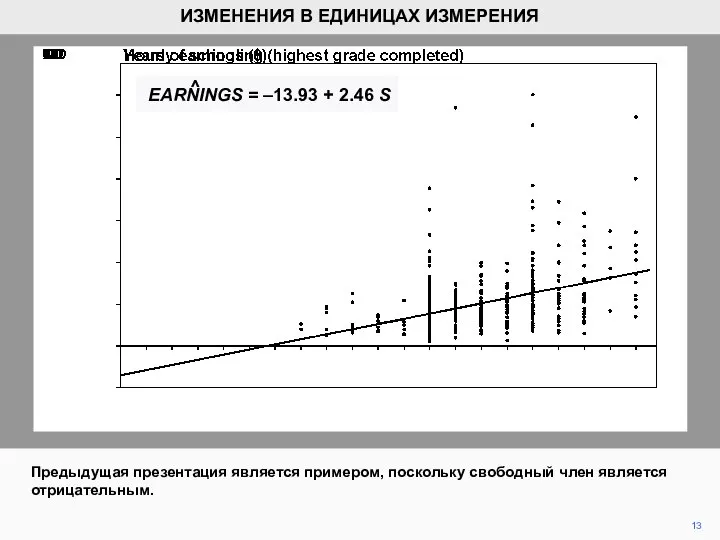
13
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ
Предыдущая презентация является примером, поскольку свободный член является отрицательным.
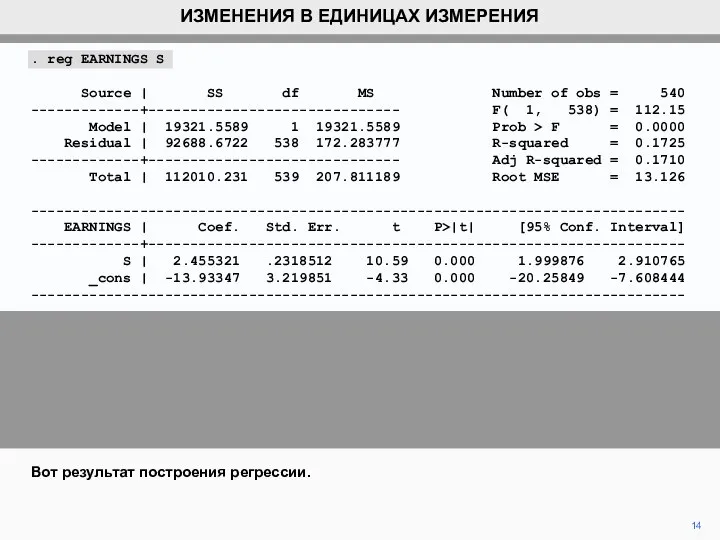
EARNINGS = –13.93 + 2.46 S
^

14
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ
Вот результат построения регрессии.
. reg EARNINGS S
Source | SS df MS Number of obs = 540
-------------+------------------------------ F( 1, 538) = 112.15
Model | 19321.5589 1 19321.5589 Prob > F = 0.0000
Residual | 92688.6722 538 172.283777 R-squared = 0.1725
-------------+------------------------------ Adj R-squared = 0.1710
Total | 112010.231 539 207.811189 Root MSE = 13.126
------------------------------------------------------------------------------
EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
S | 2.455321 .2318512 10.59 0.000 1.999876 2.910765
_cons | -13.93347 3.219851 -4.33 0.000 -20.25849 -7.608444
------------------------------------------------------------------------------

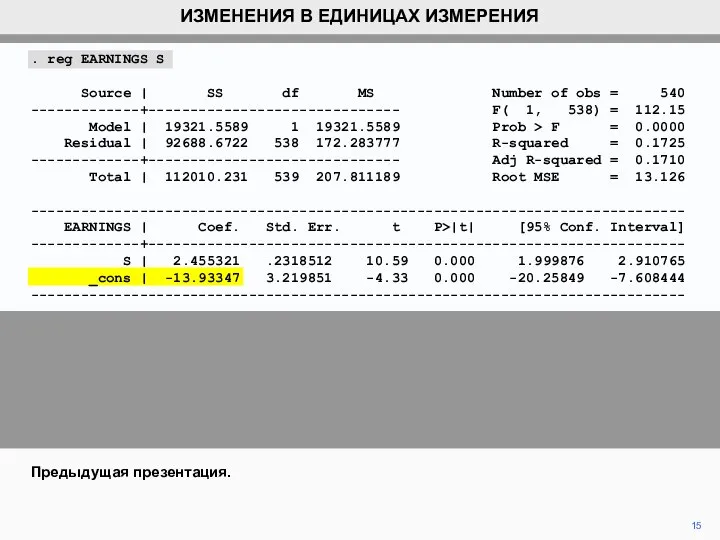
15
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ
Предыдущая презентация.
. reg EARNINGS S
Source | SS df MS Number of obs = 540
-------------+------------------------------ F( 1, 538) = 112.15
Model | 19321.5589 1 19321.5589 Prob > F = 0.0000
Residual | 92688.6722 538 172.283777 R-squared = 0.1725
-------------+------------------------------ Adj R-squared = 0.1710
Total | 112010.231 539 207.811189 Root MSE = 13.126
------------------------------------------------------------------------------
EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
S | 2.455321 .2318512 10.59 0.000 1.999876 2.910765
_cons | -13.93347 3.219851 -4.33 0.000 -20.25849 -7.608444
------------------------------------------------------------------------------

16
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ
Можно справиться с этой проблемой, определив X* как отклонение X от его среднего значения.

17
Заметим, что по определению сумма Xi* равна 0, и, следовательно, среднее значение X* равно 0.
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ

18
Если мы ищем уравнение регрессии Y от X* место X, то коэффициент наклона не изменяется.
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ

19
Теперь свободный член представляет собой среднее значение Y при среднем значении X.
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ

20
Мы находим среднее значение выборки (в Stata мы используем команду «sum»). Мы находим, что среднее составляет 13.67 лет, и мы определяем новую переменную SDEV путем вычитания 13.67 из S.
------------------------------------------------------------------------------
. sum S
Variable | Obs Mean Std. Dev. Min Max
-------------+--------------------------------------------------------
S | 540 13.67222 2.438476 7 20
. gen SDEV = S - 13.67
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ

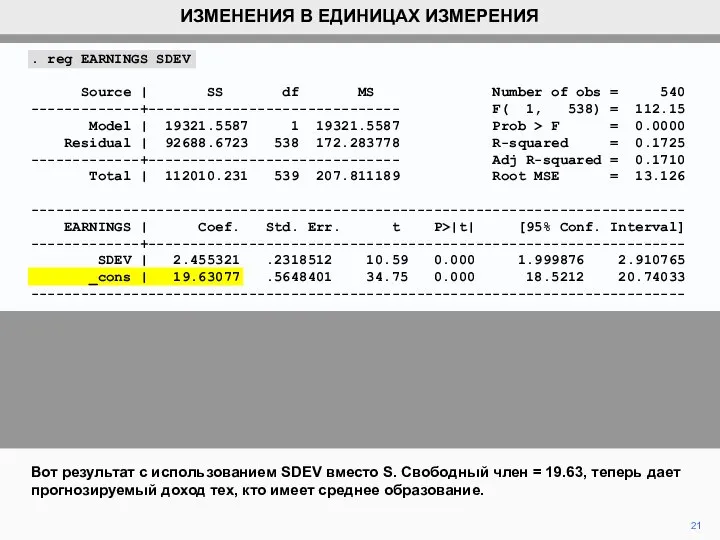
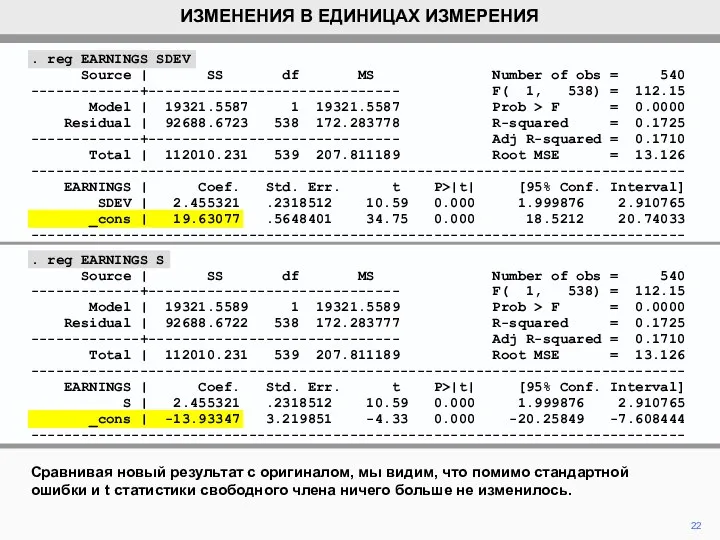
21
Вот результат с использованием SDEV вместо S. Свободный член = 19.63, теперь дает прогнозируемый доход тех, кто имеет среднее образование.
. reg EARNINGS SDEV
Source | SS df MS Number of obs = 540
-------------+------------------------------ F( 1, 538) = 112.15
Model | 19321.5587 1 19321.5587 Prob > F = 0.0000
Residual | 92688.6723 538 172.283778 R-squared = 0.1725
-------------+------------------------------ Adj R-squared = 0.1710
Total | 112010.231 539 207.811189 Root MSE = 13.126
------------------------------------------------------------------------------
EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
SDEV | 2.455321 .2318512 10.59 0.000 1.999876 2.910765
_cons | 19.63077 .5648401 34.75 0.000 18.5212 20.74033
------------------------------------------------------------------------------
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ

22
Сравнивая новый результат с оригиналом, мы видим, что помимо стандартной ошибки и t статистики свободного члена ничего больше не изменилось.
ИЗМЕНЕНИЯ В ЕДИНИЦАХ ИЗМЕРЕНИЯ
. reg EARNINGS SDEV
Source | SS df MS Number of obs = 540
-------------+------------------------------ F( 1, 538) = 112.15
Model | 19321.5587 1 19321.5587 Prob > F = 0.0000
Residual | 92688.6723 538 172.283778 R-squared = 0.1725
-------------+------------------------------ Adj R-squared = 0.1710
Total | 112010.231 539 207.811189 Root MSE = 13.126
------------------------------------------------------------------------------
EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval]
SDEV | 2.455321 .2318512 10.59 0.000 1.999876 2.910765
_cons | 19.63077 .5648401 34.75 0.000 18.5212 20.74033
------------------------------------------------------------------------------
. reg EARNINGS S
Source | SS df MS Number of obs = 540
-------------+------------------------------ F( 1, 538) = 112.15
Model | 19321.5589 1 19321.5589 Prob > F = 0.0000
Residual | 92688.6722 538 172.283777 R-squared = 0.1725
-------------+------------------------------ Adj R-squared = 0.1710
Total | 112010.231 539 207.811189 Root MSE = 13.126
------------------------------------------------------------------------------
EARNINGS | Coef. Std. Err. t P>|t| [95% Conf. Interval]
S | 2.455321 .2318512 10.59 0.000 1.999876 2.910765
_cons | -13.93347 3.219851 -4.33 0.000 -20.25849 -7.608444
------------------------------------------------------------------------------