Содержание
- 2. Задания на лабораторную работу № 5 Создать программы на языке Java для нахождения корней уравнений с
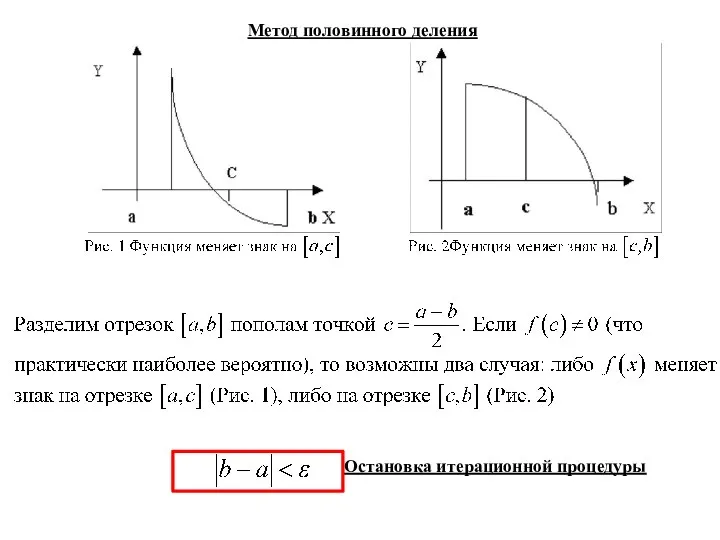
- 3. Метод половинного деления Остановка итерационной процедуры
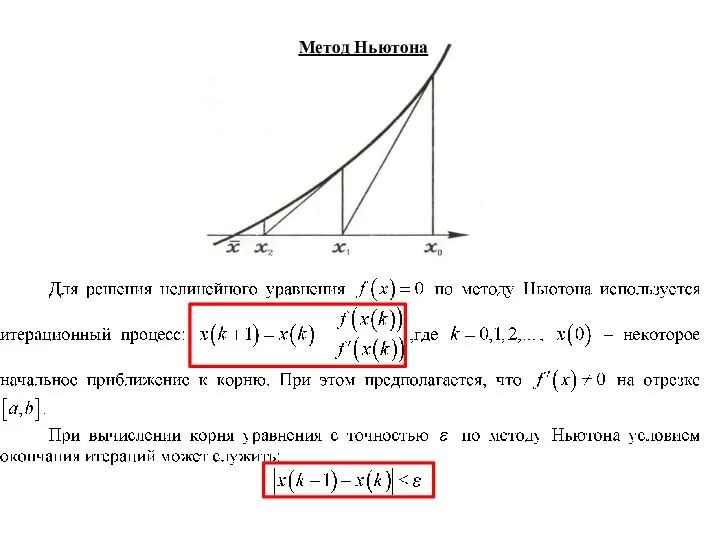
- 4. Метод Ньютона
- 5. Метод простой итерации При этом задача сводится к нахождению абсциссы точки - пересечения прямой - и
- 6. Задание: получить методами половинного деления, простой итерации и Ньютона корень уравнения с точностью 0,01;0,001;0,00001;0,0000001. Сделать сравнение
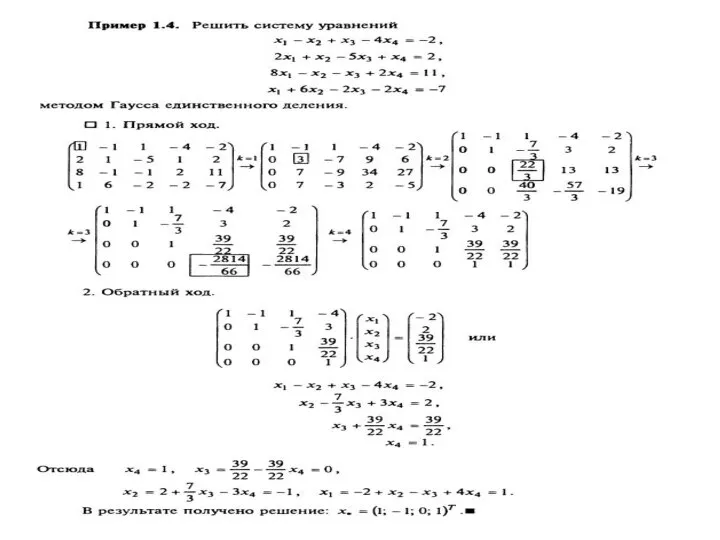
- 7. Метод Гаусса
- 10. Получение обратной матрицы Обратной матрицей к матрице A называется матрица A-1, для которой выполнено соотношение: Из
- 11. Решив полученную систему, например методом Гаусса, мы получим первый столбец обратной матрицы A–1. Чтобы получить первый
- 13. Скачать презентацию







 Библиотека, хранилище сокровищ цивилизации
Библиотека, хранилище сокровищ цивилизации Организация работы библиотеки в социальных сетях и на официальном сайте образовательной организации, МБОУ Сеяхинская ШИ
Организация работы библиотеки в социальных сетях и на официальном сайте образовательной организации, МБОУ Сеяхинская ШИ Информационная система салона релаксации
Информационная система салона релаксации Голоса выставочной индустрии. Шаблон
Голоса выставочной индустрии. Шаблон Создание и использование Актор Классов. Лекция 3
Создание и использование Актор Классов. Лекция 3 Интернет за и против. Научно–исследовательская работа
Интернет за и против. Научно–исследовательская работа Морфологический анализ
Морфологический анализ Локальные компьютерные сети (интерактивный плакат)
Локальные компьютерные сети (интерактивный плакат) Атаки на информационные ресурсы и защита от них. Компьютерные атаки
Атаки на информационные ресурсы и защита от них. Компьютерные атаки Беспроводная среда передачи данных
Беспроводная среда передачи данных Изучение функционирования системы
Изучение функционирования системы Цифровые технологии в трехмерном моделировании
Цифровые технологии в трехмерном моделировании Frozen активации. AR маска
Frozen активации. AR маска Кибер безопасность
Кибер безопасность Гипертекстовые системы
Гипертекстовые системы MeisterTask — онлайн-сервис для управления задачами/проектами
MeisterTask — онлайн-сервис для управления задачами/проектами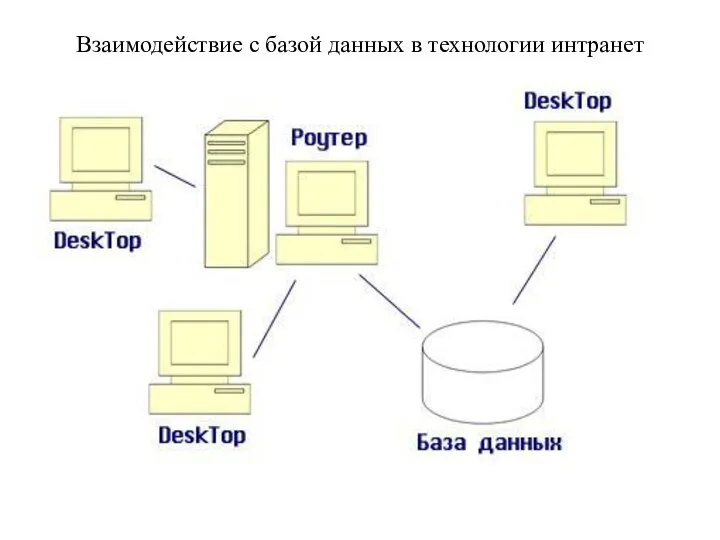 Взаимодействие с базой данных в технологии интранет
Взаимодействие с базой данных в технологии интранет Скрин 1 на проверку
Скрин 1 на проверку Telegram-бот Медицинский консультант
Telegram-бот Медицинский консультант Алгоритм по настройкам интернет
Алгоритм по настройкам интернет Информационные и транспортные услуги. 2-курс. Занятие 08
Информационные и транспортные услуги. 2-курс. Занятие 08 Эталонная модель открытых систем
Эталонная модель открытых систем Классы String, Fstream. Тема 9
Классы String, Fstream. Тема 9 Алгебра логики
Алгебра логики Free PPT templates
Free PPT templates Урок – игра “Кодирование числовой информации”
Урок – игра “Кодирование числовой информации” Основы программирования. Лабораторная работа №1
Основы программирования. Лабораторная работа №1 Типы кабелей и их характеристики. Типы линий и каналов связи
Типы кабелей и их характеристики. Типы линий и каналов связи