Содержание
- 2. Кратчайший путь в неориентированном графе без весов
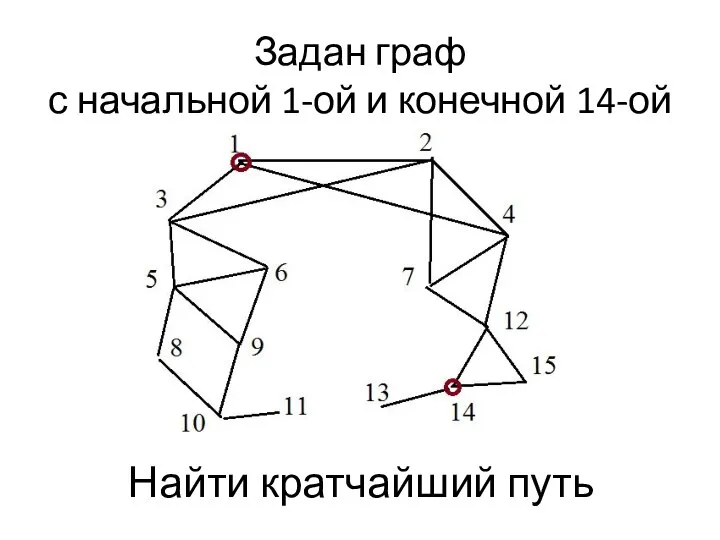
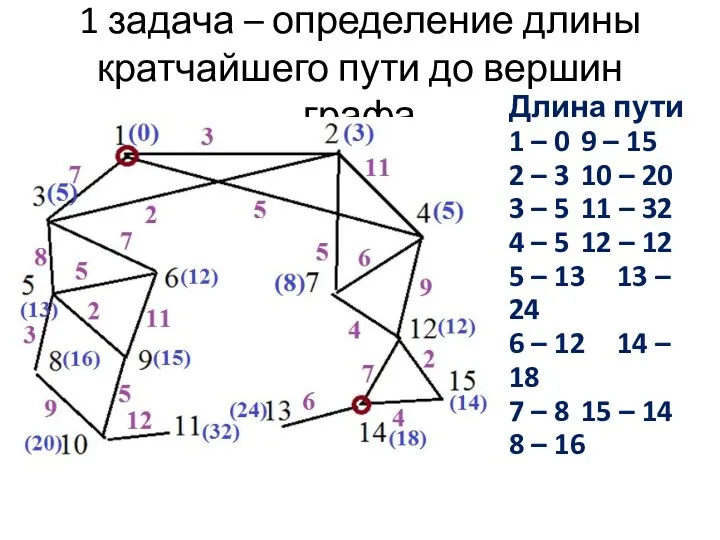
- 3. Задан граф с начальной 1-ой и конечной 14-ой Найти кратчайший путь
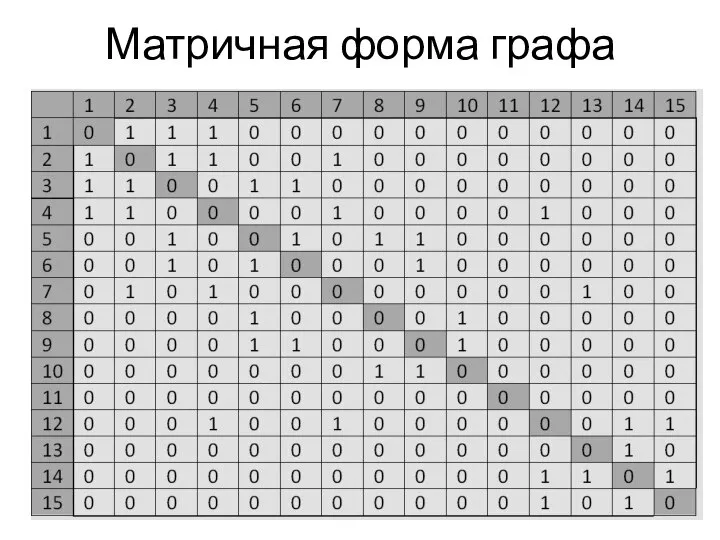
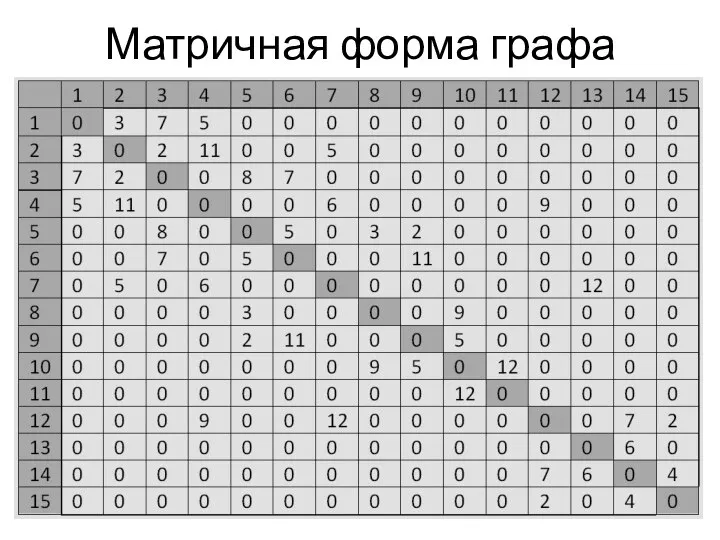
- 4. Матричная форма графа
- 5. Ввод данных int main() { int G[100][100], // граф транспортной сети I,j,n, // n – число
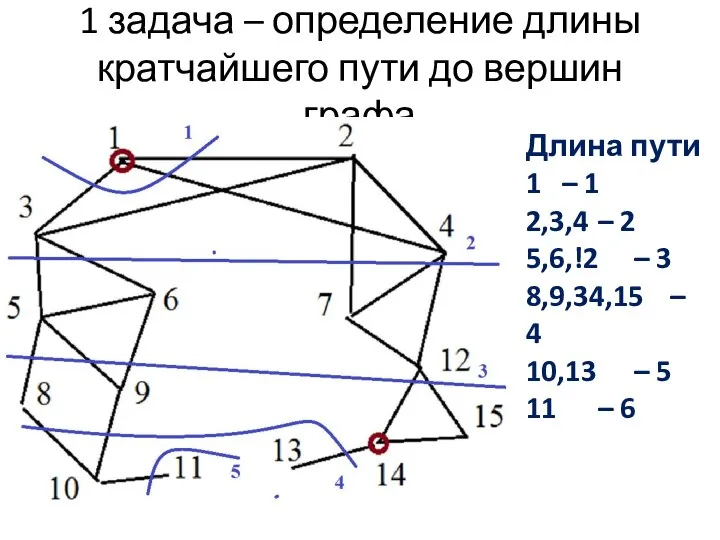
- 6. 1 задача – определение длины кратчайшего пути до вершин графа Длина пути 1 – 1 2,3,4
- 7. Oпределение длины кратчайшего пути int r[100]={0}, // 0 – расстояние не определено ob[100], // обработанные вершины
- 8. 2 задача - Анализ вектора расстояний if (r[k_p]==0) {cout int jul[100], // кратчайший путь m=k_p; //
- 9. Кратчайший путь в неориентированном графе с весами
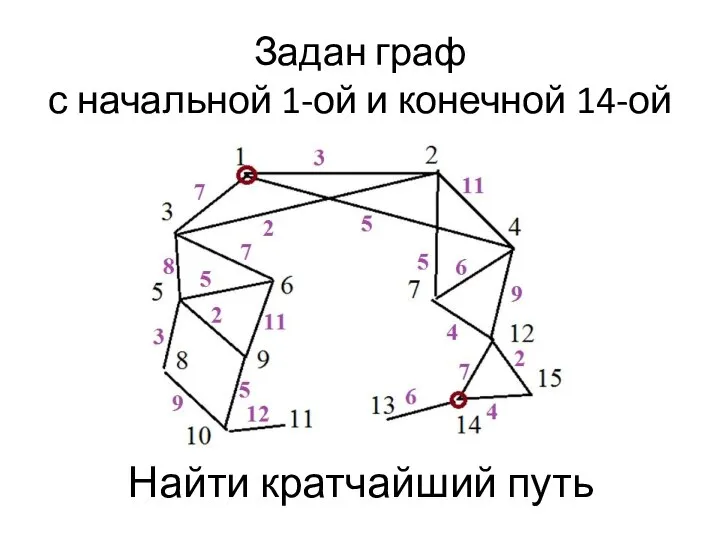
- 10. Задан граф с начальной 1-ой и конечной 14-ой Найти кратчайший путь
- 11. Матричная форма графа
- 12. Ввод данных int main() { int G[100][100], // граф транспортной сети I,j,n, // n – число
- 13. 1 задача – определение длины кратчайшего пути до вершин графа Длина пути 1 – 0 9
- 14. Oпределение длины кратчайшего пути int r[100]={-1}, // -1 – расстояние не определено r[n_p]=0; // кратчайший путь
- 15. 2 задача - Анализ вектора расстояний if (r[k_p]==-1) {cout int jul[100], // кратчайший путь m=k_p; //
- 17. Скачать презентацию

![Ввод данных int main() { int G[100][100], // граф транспортной сети I,j,n,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1154617/slide-4.jpg)
![Oпределение длины кратчайшего пути int r[100]={0}, // 0 – расстояние не определено](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1154617/slide-6.jpg)
![2 задача - Анализ вектора расстояний if (r[k_p]==0) {cout int jul[100], //](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1154617/slide-7.jpg)

![Ввод данных int main() { int G[100][100], // граф транспортной сети I,j,n,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1154617/slide-11.jpg)
![Oпределение длины кратчайшего пути int r[100]={-1}, // -1 – расстояние не определено](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1154617/slide-13.jpg)
![2 задача - Анализ вектора расстояний if (r[k_p]==-1) {cout int jul[100], //](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1154617/slide-14.jpg)
 Инжиниринг биотехнологических процессов и систем. (Лекция 1)
Инжиниринг биотехнологических процессов и систем. (Лекция 1) Оформление заявления на получение водительского удостоверения
Оформление заявления на получение водительского удостоверения Лого на доработку
Лого на доработку Летающий Автомобиль
Летающий Автомобиль Знаковые модели моделирование и формализация
Знаковые модели моделирование и формализация Вечная тетрадь, надежно хранит Ваши записи в облаке
Вечная тетрадь, надежно хранит Ваши записи в облаке Стайный алгоритм
Стайный алгоритм Путешествие по стране моделирование
Путешествие по стране моделирование Мобильные технологии поглощают мир. Плюсы и минусы
Мобильные технологии поглощают мир. Плюсы и минусы Overview of TF Domains
Overview of TF Domains Изучение работы программируемых логических контроллеров. Лабораторная работа №1
Изучение работы программируемых логических контроллеров. Лабораторная работа №1 Основы информационной безопасности
Основы информационной безопасности IT технологии в гостницах
IT технологии в гостницах Табличный процессор Excel: составление формул, функции. Работа с листом и данными, оформление таблицы (Лекция 3)
Табличный процессор Excel: составление формул, функции. Работа с листом и данными, оформление таблицы (Лекция 3) Коммуникативные модели в интернете
Коммуникативные модели в интернете ICQ. Functions
ICQ. Functions Информационная подготовка
Информационная подготовка Двоичное представление информации в компьютере. Представление чисел в компьютере
Двоичное представление информации в компьютере. Представление чисел в компьютере Техническое задание на проектирование персонажа
Техническое задание на проектирование персонажа История первых ЭВМ
История первых ЭВМ Kofax. Настраиваемые (обучаемые) локаторы для счет-фактуры
Kofax. Настраиваемые (обучаемые) локаторы для счет-фактуры Понятие и виды компьютерных сетей
Понятие и виды компьютерных сетей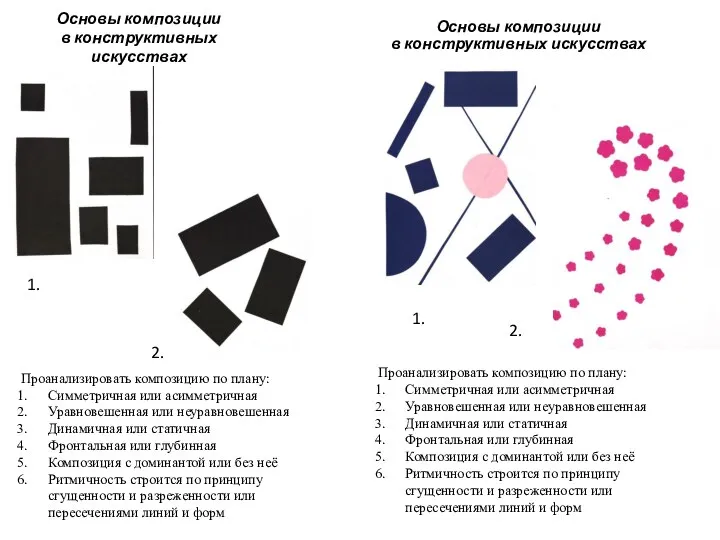 Основы композиции в конструктивных искусствах
Основы композиции в конструктивных искусствах Почтовый лист и современные бланки
Почтовый лист и современные бланки Игра на реакцию Уклонись от предмета
Игра на реакцию Уклонись от предмета Алгоритм Ветвление. Трассировка
Алгоритм Ветвление. Трассировка Информационное обеспечение системы управления персоналом
Информационное обеспечение системы управления персоналом Manhunt for killer
Manhunt for killer