Л5 Обработка инф. Основы логики. Алгоритмы ИС 2021

1. Обработка информации
Любая информация может обрабатываться компьютером, если она представлена в двоичной знаковой системе. Информация в двоичном компьютерном коде представляет собой последовательность нулей и единиц, т.е. данные.
Для того, чтобы компьютер «знал», что ему делать с данными, как их обрабатывать, он должен получить определенную команду (инструкцию). Таким образом составляется алгоритм решения задачи, т.е. определенная последовательность команд.

Логика - это фундаментальная основа информатики как науки. Элементы и основы математической логики заложены в логические элементы и логические устройства ЭВМ, в основы алгоритмизации и языки программирования, в процедуры поиска информации в базах данных и в сети Интернет, а также в системах логического программирования, базах знаний и экспертных системах на ЭВМ.
2. Основы логики

Логическое выражение - устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты).
Сложное логическое выражение - логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Высказывания могут быть истинными (1) ИЛИ ложными (0).

Логические операции и таблицы истинности

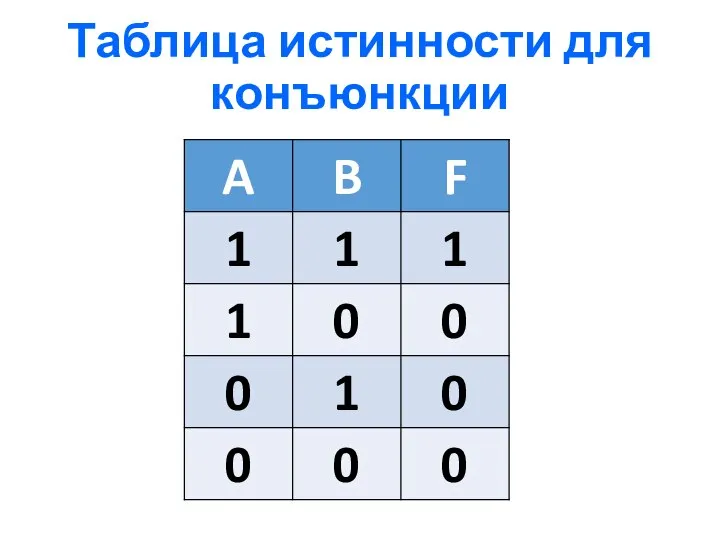
1) Логическое умножение или конъюнкция (И)
Конъюнкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложенное выражение ложно.
Обозначение: F = A & B или F =A Λ B

Таблица истинности для конъюнкции

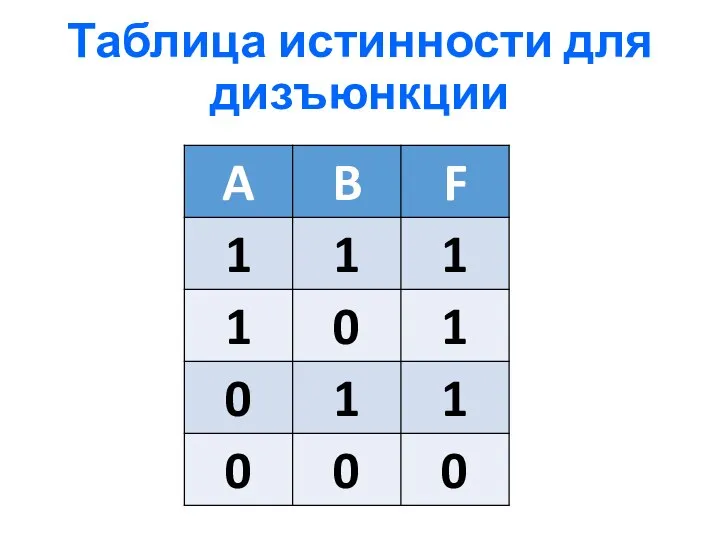
2) Логическое сложение или дизъюнкция (ИЛИ)
Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выражения ложны.
Обозначение: F = A v B.

Таблица истинности для дизъюнкции

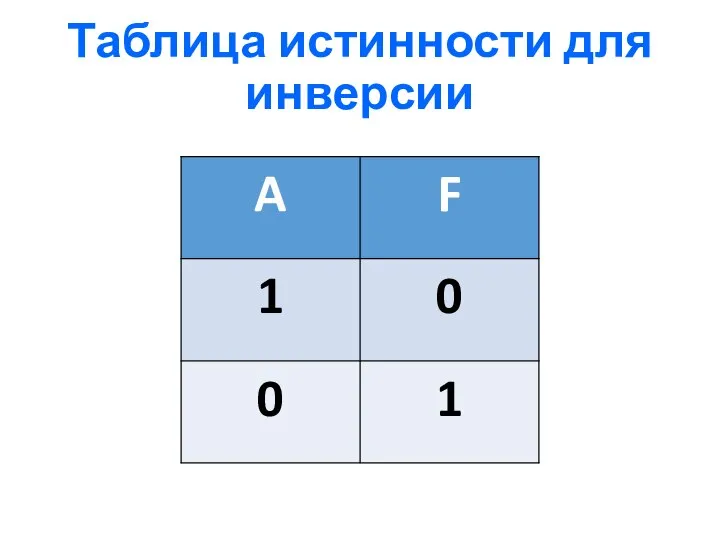
3) Логическое отрицание или инверсия (НЕ)
Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Обозначение: F = ¬A.

Таблица истинности для инверсии

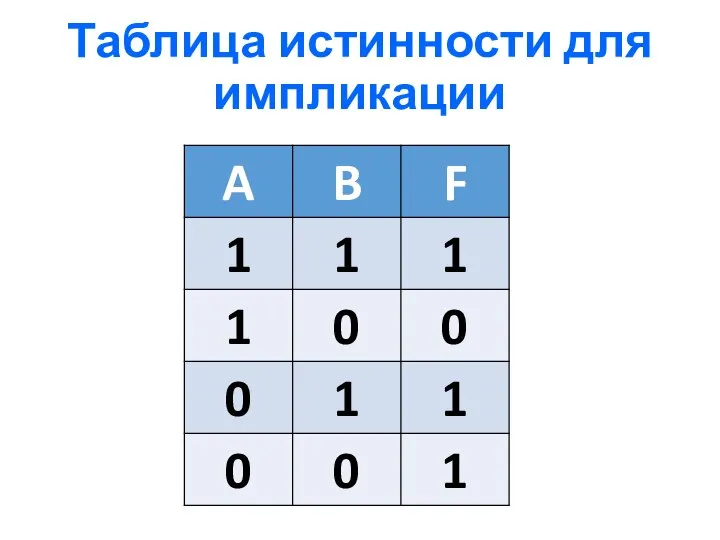
4) Логическое следование или импликация
Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.

Таблица истинности для импликации

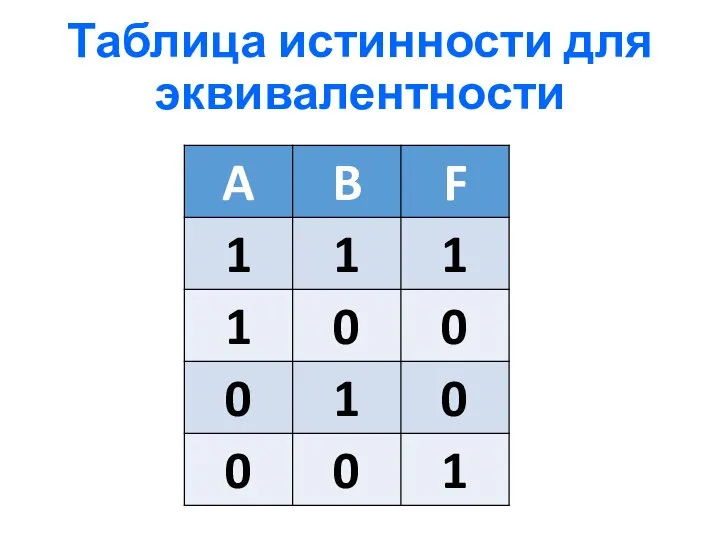
5) Логическая равнозначность или эквивалентность
Эквивалентность - это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
«A ↔ B» истинно тогда и только тогда, когда А и B равны.
Обозначение: F = A ↔ B или
F = A ≡ B

Таблица истинности для эквивалентности

3. АЛГОРИТМЫ
Алгоритм - это точное предписание о последовательности действий, которые должны быть произведены для получения результата.
Алгоритмический язык - это формальный язык для записи алгоритмов, который включает в себя набор символов (алфавит языка), систему правил связи символов для образования «слов», с помощью которых представляются отдельные составляющие компоненты языка (синтаксис языка), и систему правил истолкования слов языка (семантику).

Свойства алгоритмов

1. Дискретность алгоритма
Свойство алгоритма, означающее, что процесс решения задачи, определяемый алгоритмом, расчленён на отдельные элементарные действия (шаги) и, соответственно, алгоритм представляет последовательность указаний, команд, определяющих порядок выполнения шагов процесса.

Это свойство означает, что каждая команда алгоритма должна быть понятна исполнителю, не оставлять места для её неоднозначного толкования и неопределённого исполнения.
2. Определённость алгоритма

3. Результативность алгоритма
Свойство алгоритма, состоящее в том, что он всегда приводит к результату через конечное, возможно, очень большое число шагов.

4. Массовость алгоритма
каждый алгоритм, разработанный для решения некоторой задачи, должен быть применим для решения задач этого типа при всех допустимых значениях исходных данных.

Виды алгоритмов:
Линейный алгоритм – описание действий, которые выполняются однократно, при этом четко друг за другом;
Циклический алгоритм – описание действий, которые должны повторятся определенное количество раз или пока не выполнится условие.
Разветвляющий алгоритм – алгоритм, в котором в зависимости от условия выполняется либо одна, либо друга последовательность действий.

Программирование -
это наука, изучающая теорию и методы разработки, производства и эксплуатации программного обеспечения ЭВМ.

Язык программирования -
это способ записи программ решения различных задач на ЭВМ в понятной для компьютера форме.
Языки программирования: БЕЙСИК, ФОРТРАН, КОБОЛ, ПАСКАЛЬ, СИ, СИ+, СИ++ и др.