Содержание
- 2. Часть 1. Умножение матрицы на вектор Умножение матрицы на вектор или Задача умножения матрицы на вектор
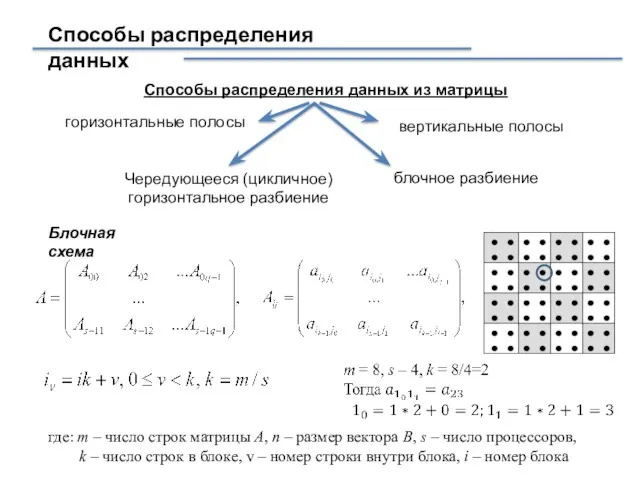
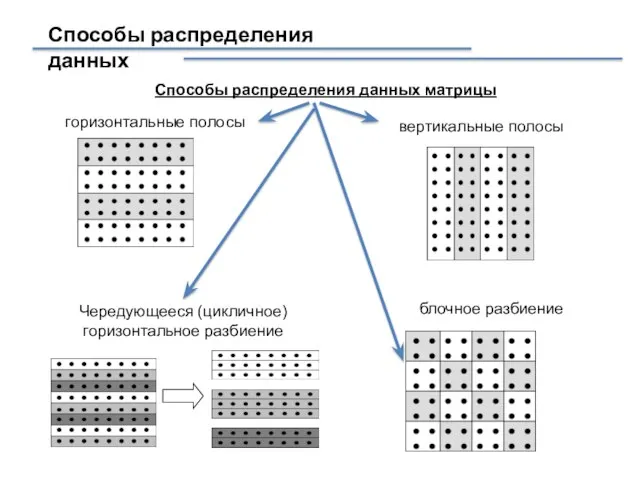
- 3. Способы распределения данных Способы распределения данных из матрицы горизонтальные полосы вертикальные полосы Чередующееся (цикличное) горизонтальное разбиение
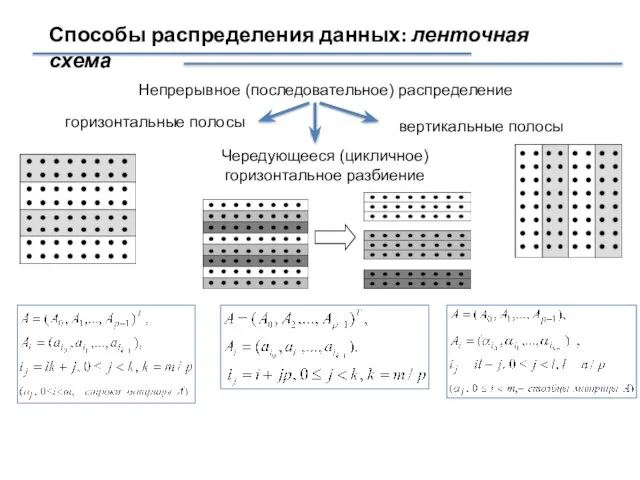
- 4. Способы распределения данных: ленточная схема Непрерывное (последовательное) распределение горизонтальные полосы вертикальные полосы Чередующееся (цикличное) горизонтальное разбиение
- 5. Последовательный алгоритм Для выполнения матрично-векторного умножения необходимо выполнить m операций вычисления скалярного произведения Трудоемкость вычислений имеет
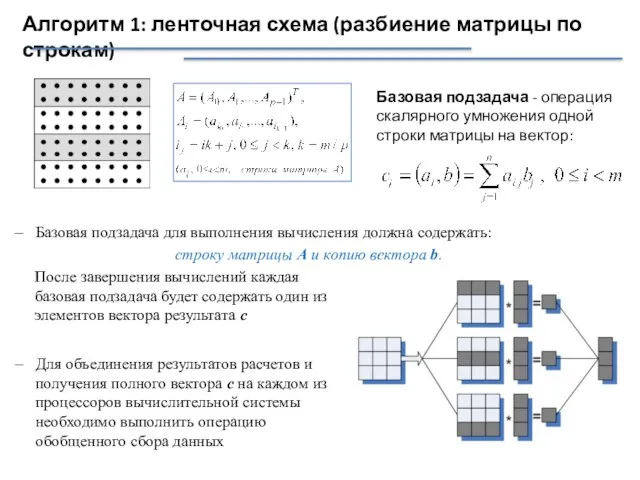
- 6. Алгоритм 1: ленточная схема (разбиение матрицы по строкам) Базовая подзадача - операция скалярного умножения одной строки
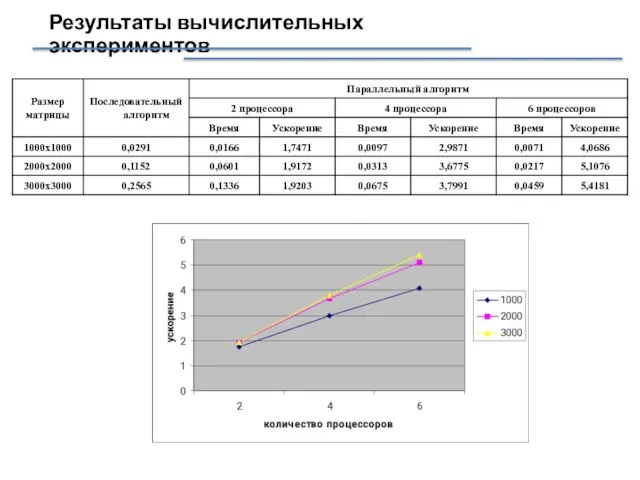
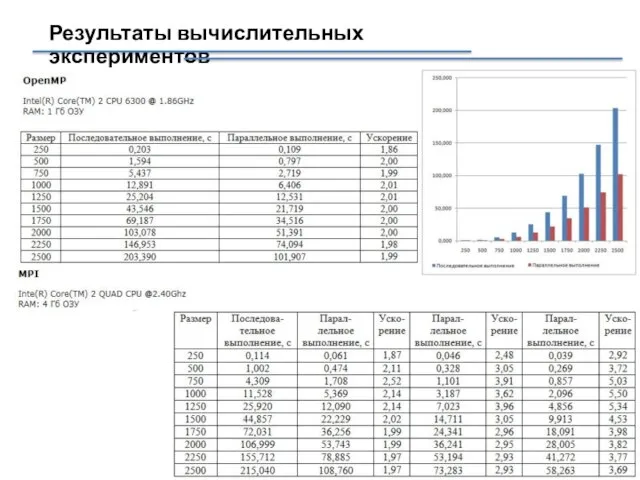
- 7. Результаты вычислительных экспериментов
- 8. Алгоритм 2: ленточная схема (разбиение матрицы по столбцам) Базовая подзадача - операция умножения столбца матрицы А
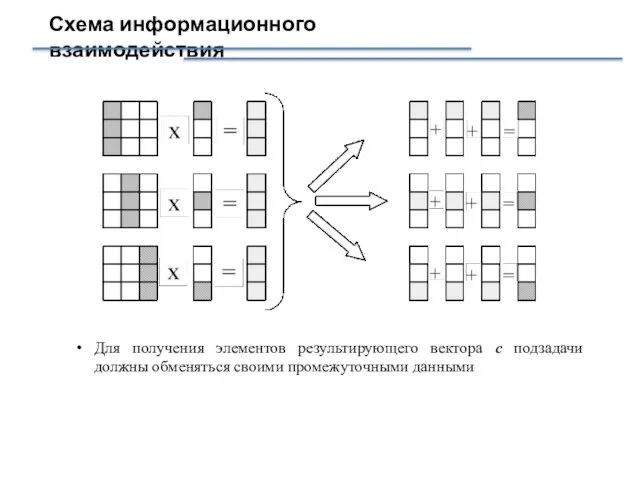
- 9. Схема информационного взаимодействия Для получения элементов результирующего вектора с подзадачи должны обменяться своими промежуточными данными
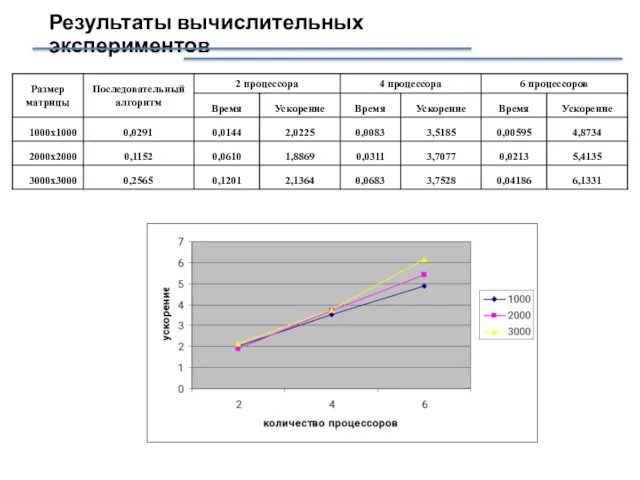
- 10. Результаты вычислительных экспериментов
- 11. Алгоритм 3: блочная схема Пусть: количество процессоров p=s·q , количество строк матрицы является кратным s: m=k·s
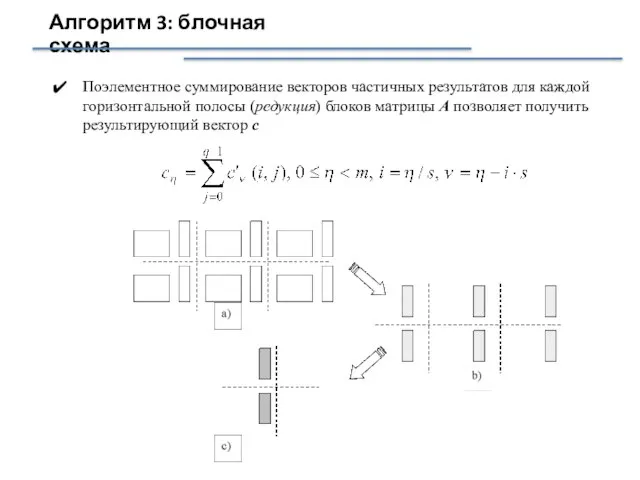
- 12. Алгоритм 3: блочная схема Поэлементное суммирование векторов частичных результатов для каждой горизонтальной полосы (редукция) блоков матрицы
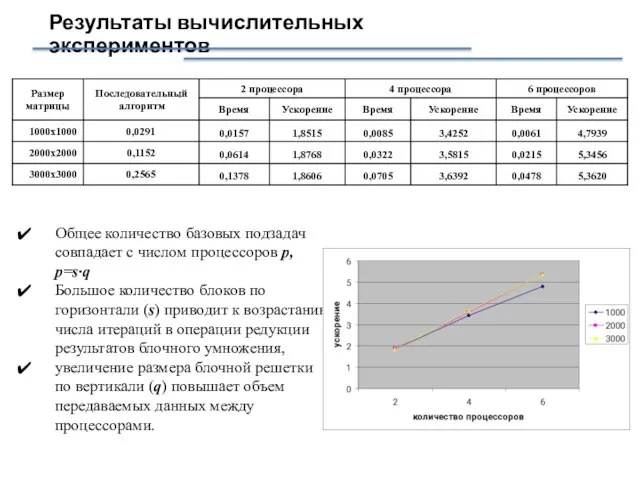
- 13. Результаты вычислительных экспериментов Общее количество базовых подзадач совпадает с числом процессоров p, p=s·q Большое количество блоков
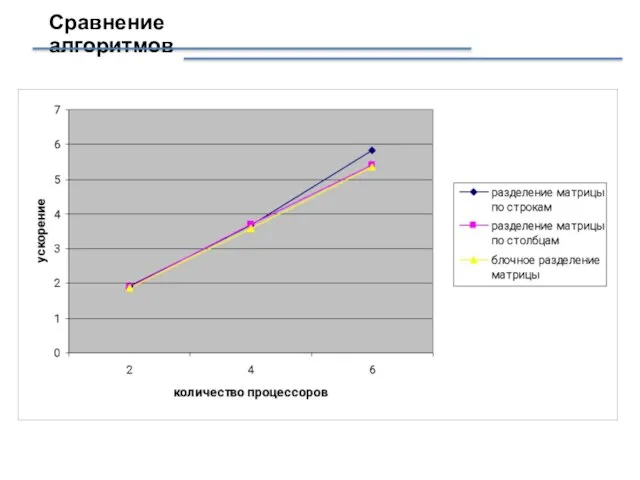
- 14. Сравнение алгоритмов
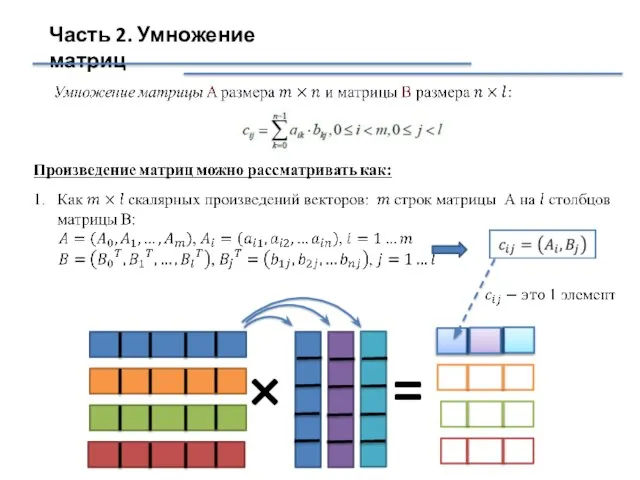
- 15. Часть 2. Умножение матриц Умножение матриц: или Задача умножения матрицы на матрицу может быть сведена к
- 16. Последовательный базовый алгоритм double MatrixA[Size][Size]; double MatrixB[Size][Size]; double MatrixC[Size][Size]; int i,j,k; ... for (i=0; i for
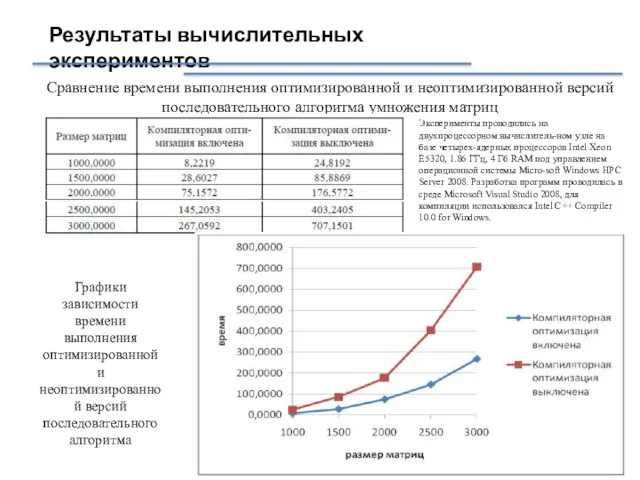
- 17. Результаты вычислительных экспериментов Эксперименты проводились на двухпроцессорном вычислитель-ном узле на базе четырех-ядерных процессоров Intel Xeon E5320,
- 18. Часть 2. Умножение матриц × =
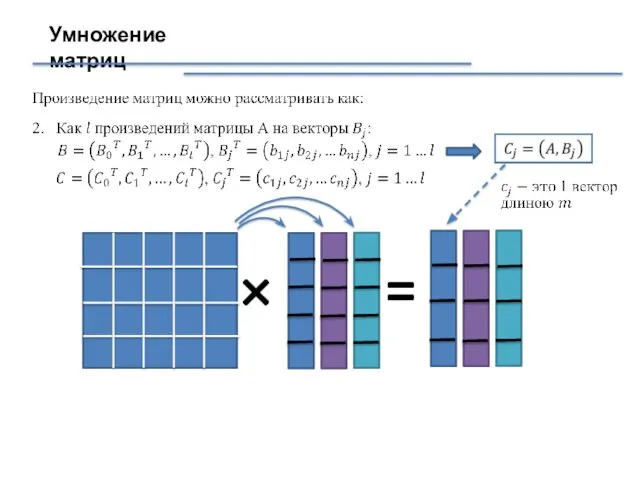
- 19. Умножение матриц × =
- 20. Умножение матриц Процесс хранит одну строку матрицы A и все столбцы матрицы B
- 21. Трудоемкость
- 22. Способы распределения данных Способы распределения данных матрицы горизонтальные полосы вертикальные полосы Чередующееся (цикличное) горизонтальное разбиение блочное
- 23. Параллельный алгоритм 1: ленточная схема Каждая подзадача содержит по одной строке матрицы А и одному столбцу
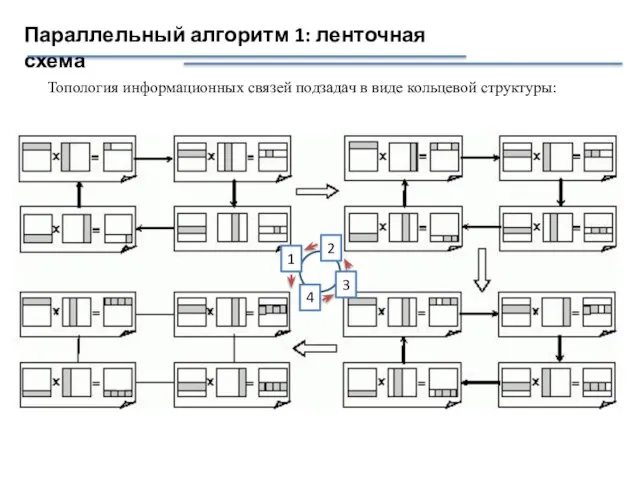
- 24. Параллельный алгоритм 1: ленточная схема Топология информационных связей подзадач в виде кольцевой структуры: 1 2 3
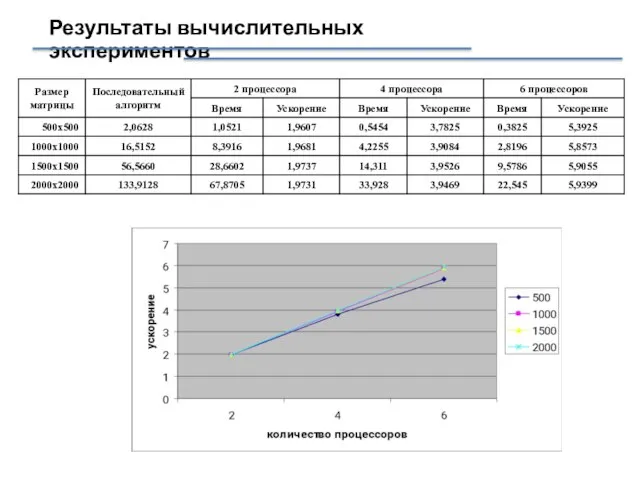
- 25. Результаты вычислительных экспериментов
- 26. Параллельный алгоритм 1: ленточная схема void MatrixMultiplicationMPI(double *&A, double *&B, double *&C, int &Size) { int
- 27. int NextProc; int PrevProc; for (p=1; p { NextProc = ProcRank+1; if (ProcRank == ProcNum-1) NextProc
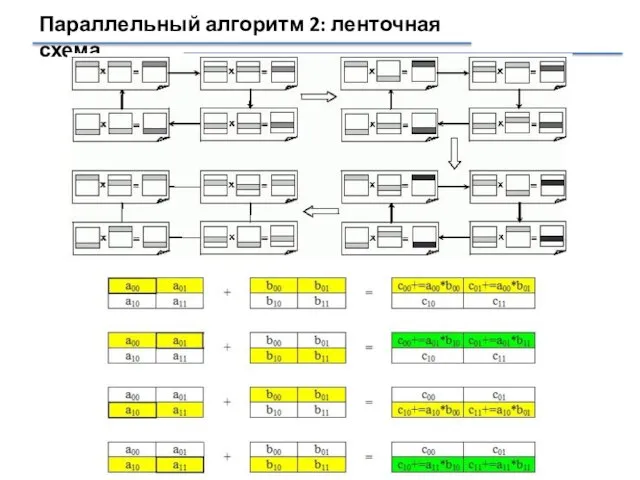
- 28. Параллельный алгоритм 2: ленточная схема Идея: распределение данных в разбиении матриц A и B по строкам
- 29. Параллельный алгоритм 2: ленточная схема
- 30. Параллельный алгоритм 2: ленточная схема Алгоритм Вначале производится рассылка в процесс ранга K элементов K-й строки
- 31. Результаты вычислительных экспериментов
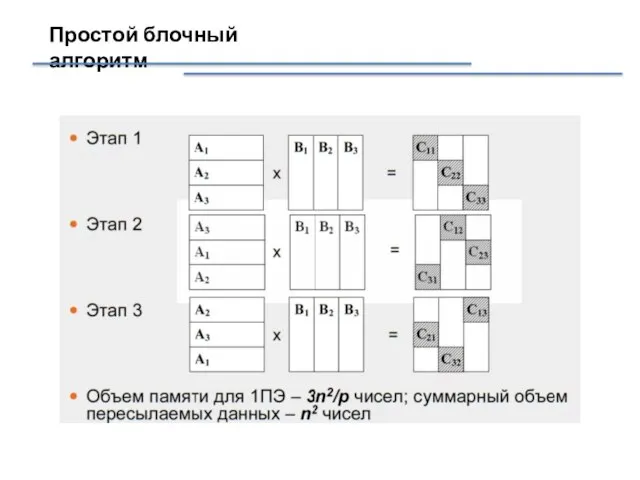
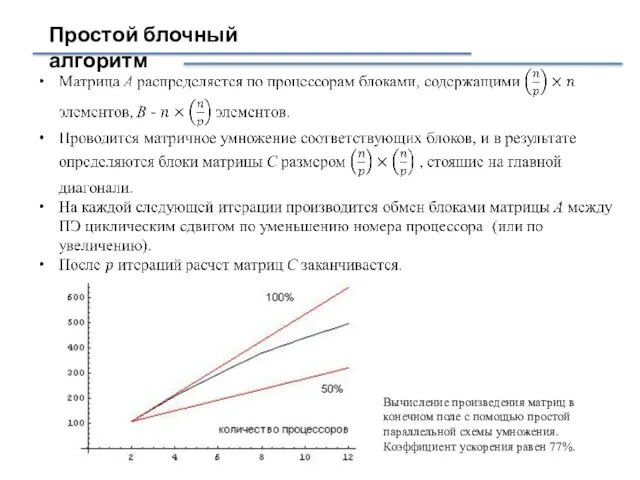
- 32. Простой блочный алгоритм
- 33. Простой блочный алгоритм Вычисление произведения матриц в конечном поле с помощью простой параллельной схемы умножения. Коэффициент
- 34. Метод Фокса Распределение данных происходит по Блочной схеме Базовая подзадача - процедура вычисления всех элементов одного
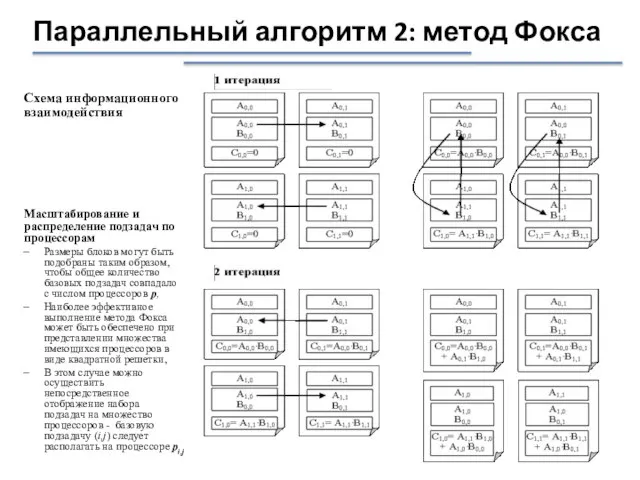
- 35. Параллельный алгоритм 2: метод Фокса Выделение информационных зависимостей - для каждой итерации l, 0≤ l блок
- 36. Схема информационного взаимодействия Параллельный алгоритм 2: метод Фокса Масштабирование и распределение подзадач по процессорам Размеры блоков
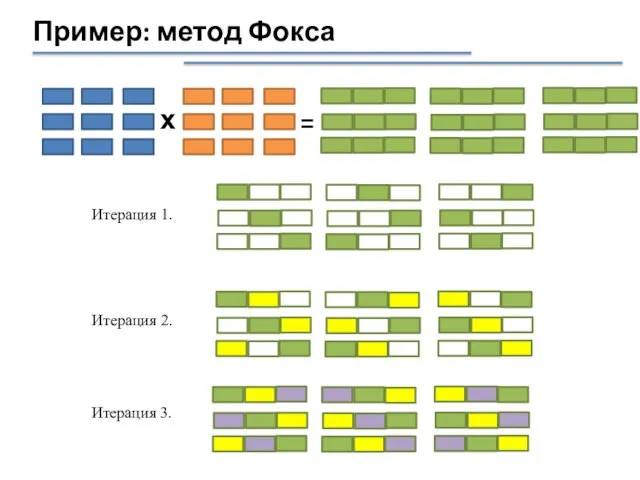
- 37. Пример: метод Фокса Итерация 1. Диагональные процессы раздают свои элементы матрицы А направо соседям, матрица В
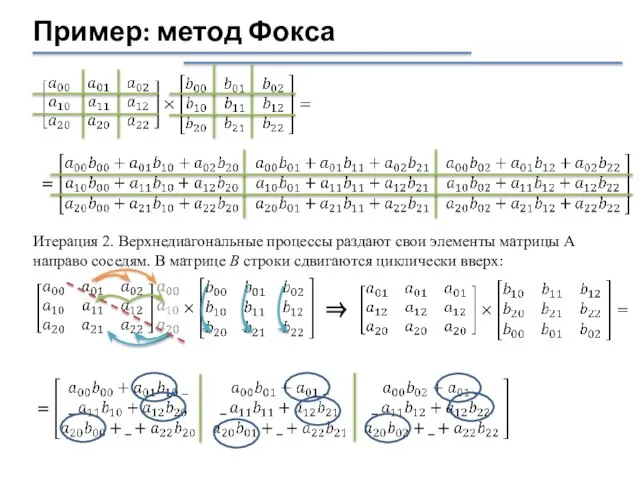
- 38. Пример: метод Фокса Итерация 2. Верхнедиагональные процессы раздают свои элементы матрицы А направо соседям. В матрице
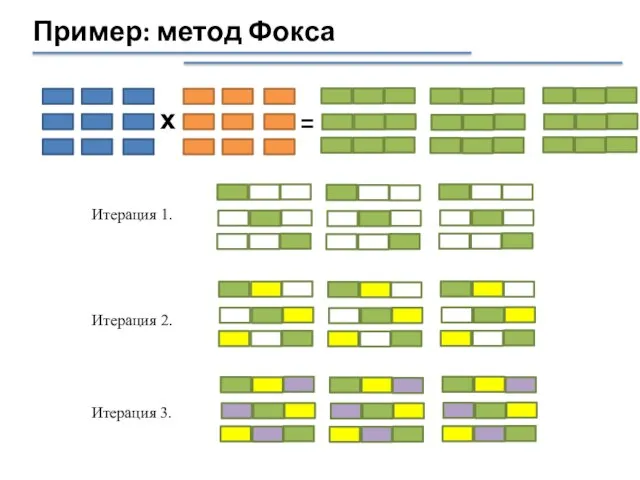
- 39. Пример: метод Фокса х = Итерация 2. Итерация 1. Итерация 3.
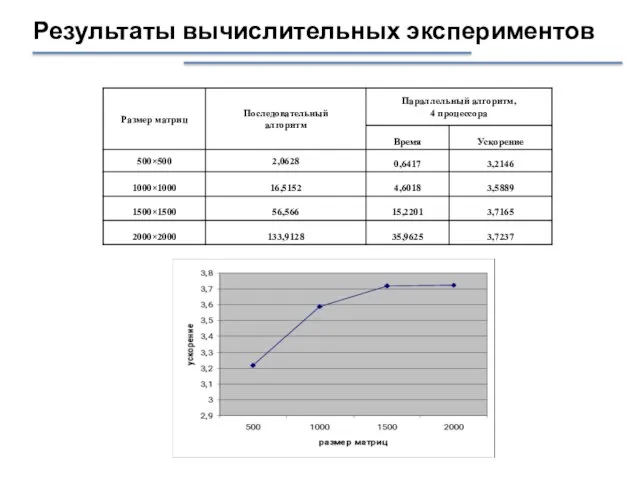
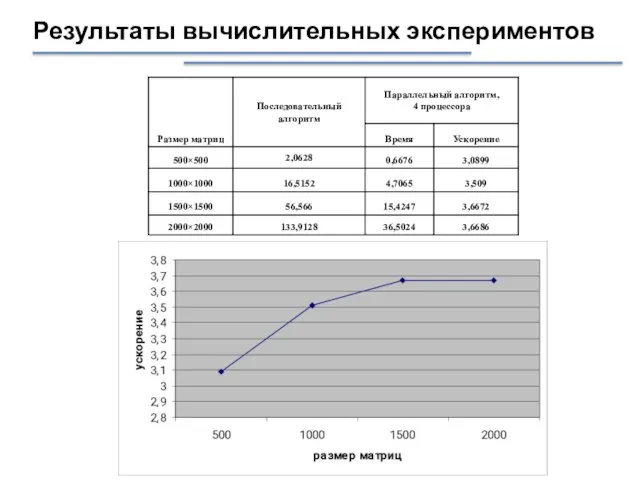
- 40. Результаты вычислительных экспериментов
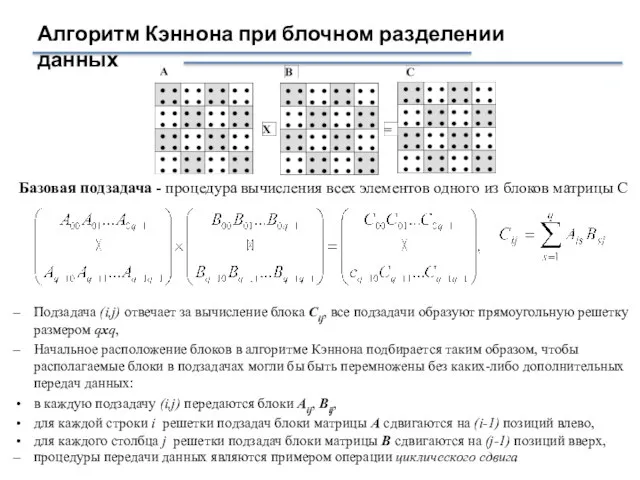
- 41. Алгоритм Кэннона при блочном разделении данных Базовая подзадача - процедура вычисления всех элементов одного из блоков
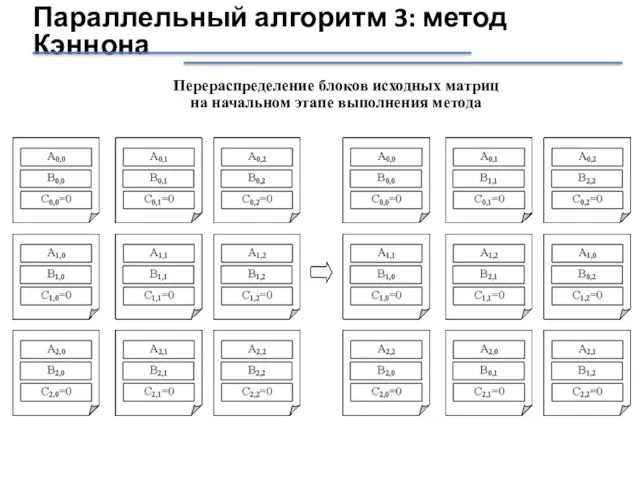
- 42. Перераспределение блоков исходных матриц на начальном этапе выполнения метода Параллельный алгоритм 3: метод Кэннона
- 43. Пример: метод Кэннона Итерация 1. Циклический сдвиг по строкам: 0-я строка на 0 элементов влево 1-я
- 44. Пример: метод Фокса х = Итерация 2. Итерация 1. Итерация 3.
- 45. Выделение информационных зависимостей В результате начального распределения в каждой базовой подзадаче будут располагаться блоки, которые могут
- 46. Результаты вычислительных экспериментов
- 48. Скачать презентацию





![Последовательный базовый алгоритм double MatrixA[Size][Size]; double MatrixB[Size][Size]; double MatrixC[Size][Size]; int i,j,k; ...](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/906018/slide-15.jpg)












 АСУТП алюминия электролизом ТРОЛЛЬ и СААТ
АСУТП алюминия электролизом ТРОЛЛЬ и СААТ Разгони свой сайт. Объединение файлов. Лекция 4
Разгони свой сайт. Объединение файлов. Лекция 4 Технологии дистанционного обучения
Технологии дистанционного обучения Передача информации
Передача информации Система счисления
Система счисления Циклы Паскаль
Циклы Паскаль Комбинация данных из нескольких таблиц
Комбинация данных из нескольких таблиц Персональный компьютер
Персональный компьютер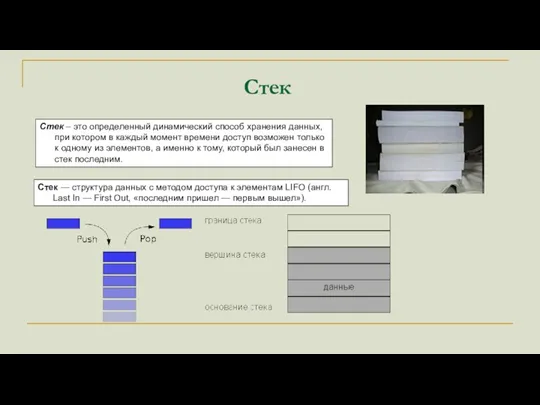 Стек. Реализация стека
Стек. Реализация стека Знакомство с интерфейсом OpenOffice.org Calc
Знакомство с интерфейсом OpenOffice.org Calc EW2-week 1
EW2-week 1 Правила ввода и решения задач с одномерными массивами. Часть 1
Правила ввода и решения задач с одномерными массивами. Часть 1 Сравнение платформ создания сайтов
Сравнение платформ создания сайтов Устройство компьютера и ноутбука. Урок 1
Устройство компьютера и ноутбука. Урок 1 Платформы для создания кроссвордов
Платформы для создания кроссвордов Одномерные массивы
Одномерные массивы Создание сборок Операционных систем
Создание сборок Операционных систем Киберспорт
Киберспорт Реляционные отношения между таблицами базы данных
Реляционные отношения между таблицами базы данных Comment obtenir une licence Microsoft office 2016 en utilisant l’adresse e-mail
Comment obtenir une licence Microsoft office 2016 en utilisant l’adresse e-mail We benchmark Booking.com app
We benchmark Booking.com app Юристы и хай-тек. Кто в Украине первым купит юридический стартап
Юристы и хай-тек. Кто в Украине первым купит юридический стартап Создание базы данных обращения клиентов в МФЦ в Microsoft Visual Studio на языка С#
Создание базы данных обращения клиентов в МФЦ в Microsoft Visual Studio на языка С# Как работает компьютерный иммунитет?
Как работает компьютерный иммунитет? Обучающее приложение для детей
Обучающее приложение для детей Прикладные информационные технологии. Информационные технологии организационного управления
Прикладные информационные технологии. Информационные технологии организационного управления В лабиринтах интернета. Анализ сообщества ВКонтакте
В лабиринтах интернета. Анализ сообщества ВКонтакте Файл. Внешняя память
Файл. Внешняя память