Линейные блочные коды

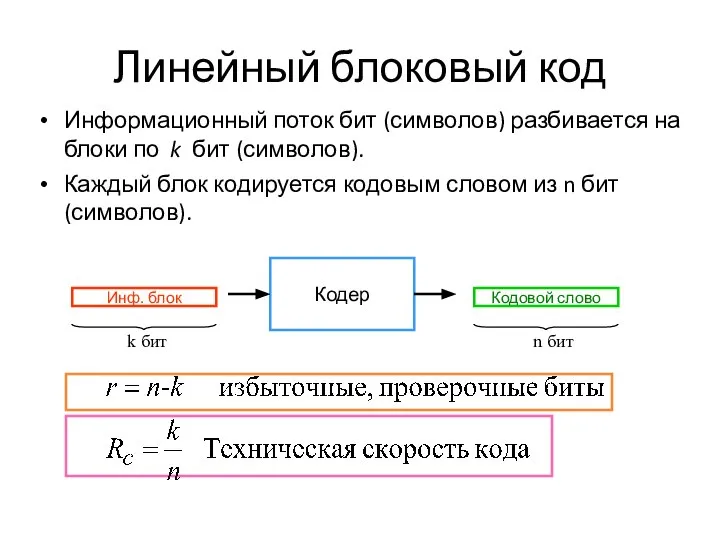
Линейный блоковый код
Информационный поток бит (символов) разбивается на блоки по k бит (символов).
Каждый блок кодируется кодовым словом из n бит (символов).

Линейный блоковый код (ЛБК)
Геометрический подход

Геометрия пространства
Пример

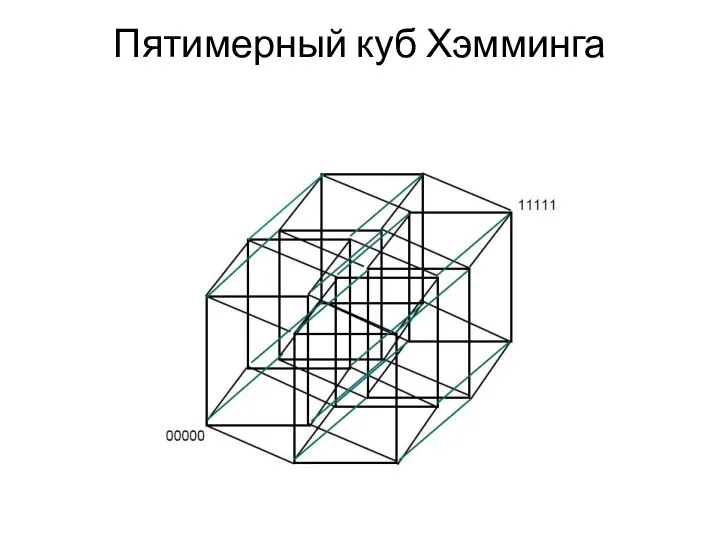
Пятимерный куб Хэмминга

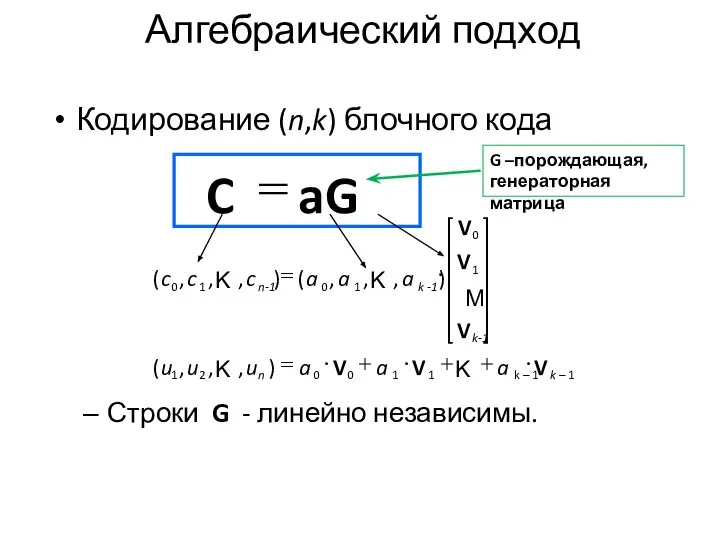
Алгебраический подход
Кодирование (n,k) блочного кода
Строки G - линейно независимы.
aG
C
=
k – 1
n
k-1
k -1
n-1
a
a
a
u
u
u
a
a
a
c
c
c
V
V
V
V
V
V
⋅
+
+
⋅
+
⋅
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅
=
k – 1
1
1
0
0
2
1
1
0
1
0
1
0
)
,
,
,
(
)
,
,
,
(
)
,
,
,
(
K
K
M
K
K
G –порождающая, генераторная матрица

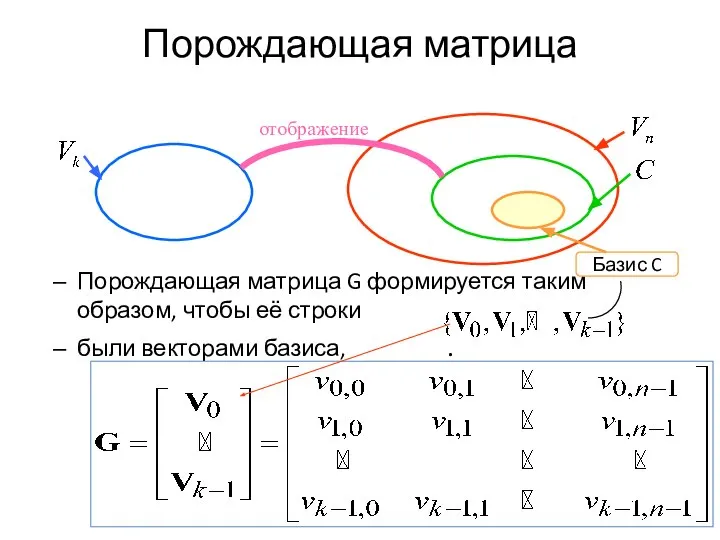
Порождающая матрица
Порождающая матрица G формируется таким образом, чтобы её строки
были векторами базиса, .

Пример
Блочный код (6,3)‏
Вектор сообщения
Слова кода

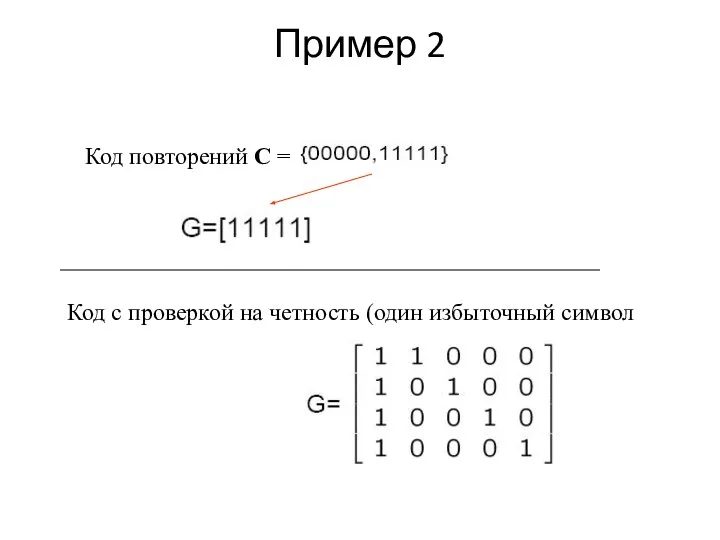
Пример 2
Код повторений С =
Код с проверкой на четность (один избыточный символ

Систематический блоковый код
Систематичный блоковый код (n,k)‏
Для систематического кода, первые (или последние) k символов являются информационными.
подматрица
)
(
матрица
единичная
]
[
k
n
k
k
k
k
k
k
−
×
=
×
=
=
P
I
I
P
G
или G = [ Ik | P]

Проверочная матрица
HGT = [ – PT | In – k][ Ik | P]T = – PT Ik + In – kPT = 0
или

Определение кода через проверочные уравнения:

Систематический код
Пусть G = [I k | P],
P = [ pi,j] - подматрица размером k×(n – k),
p1,…,pk – строки P
тогда
с = aG = (a0, … , ak – 1, p),
где p = Σj ajpj
Проверочная матрица
H = [ – PT | In – k ] = [ hi,j].
Элементы hi,j удовлетворяют системе уравнений
HaT = 0,
где a = (a0, …, ak – 1 , p0, p1, …, pn – k – 1)

Ортогональное подпространство H
Пусть код C={ci} -> G
Определим код через нуль-пространство H
C = {c ∈F: HcT = 0}
где F – поле (множество) элементов кода
Матрица H аннулирует кодовые слова
Образуется ортогональное подпространство относительно кода С

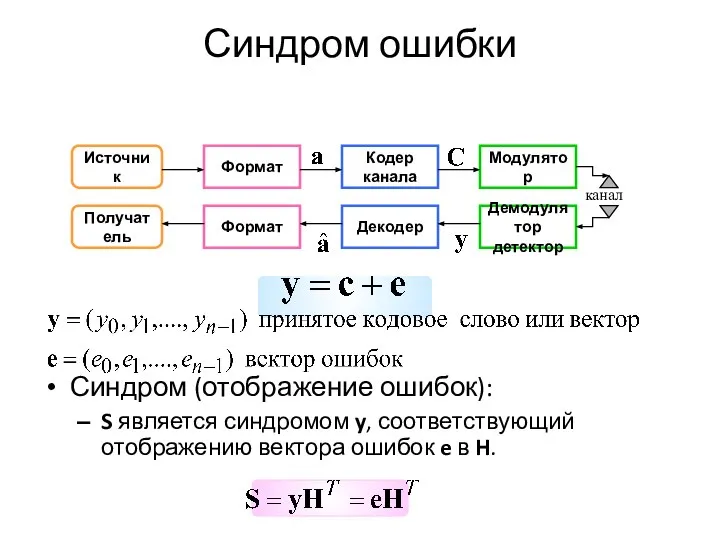
Синдром ошибки
Синдром (отображение ошибок):
S является синдромом y, соответствующий отображению вектора ошибок e в H.
Формат
Кодер канала
Модулятор
Декодер
Формат
Демодулятор
детектор
Источник
Получатель
канал

Двойственный (дуальный) код
Если С – линейный код размером k, то ортогональным или двойственным ему будет код , определяемый как
Двойственный код является (n, n - k)-кодом. Если H – это порождающая матрица двойственного кода, то матрицу H называют проверочной матрицей кода С
где

Двойственные (дуальные) коды
Пример. Троичные коды
Троичный алфавит
Операции по mod 3
Пространство
n = 4
Код (4, 2)
Полный код

Комбинаторный подход
Пространство Хэмминга
Пространство Xn – вместе с метрикой d называется метрическим пространством Хэмминга

Вес Хэмминга
Вес Хэмминга вектора U, обозначается как wt(U), определяется как число ненулевых элементов в U

Комбинаторные соотношения
. Число различных кодовых слов длины n и веса t
Если 0 ≤t ≤n и с – кодовое слово длины n, тогда число различных слов длины n и расстоянием по отношению к c не более t равно

Комбинаторно-геометрический подход
Сферическая модель
Определим множество
которое описывает геометрическую фигуру шара радиусом ρ с центром в сi
Сфера шара описывается множеством
Количество элементов шара или мощность шара
Vol(c,ρ) =

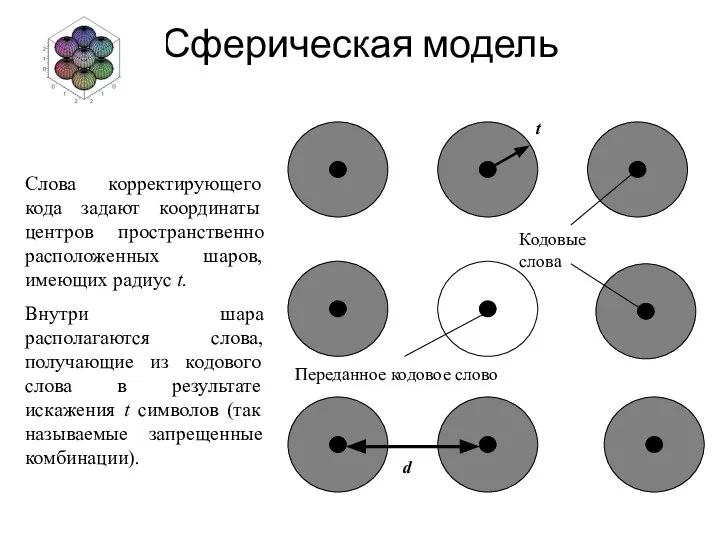
Сферическая модель
Слова корректирующего кода задают координаты центров пространственно расположенных шаров, имеющих радиус t.
Внутри шара располагаются слова, получающие из кодового слова в результате искажения t символов (так называемые запрещенные комбинации).

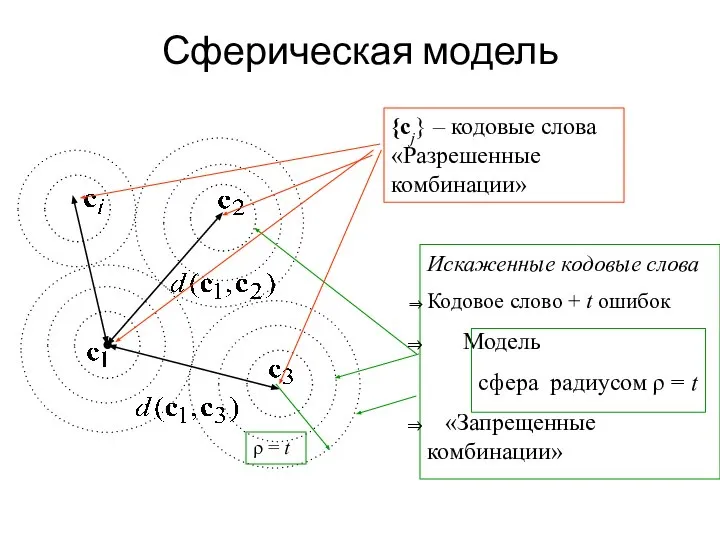
Сферическая модель
Искаженные кодовые слова
Кодовое слово + t ошибок
Модель
сфера радиусом ρ = t
«Запрещенные комбинации»
{сj} – кодовые слова «Разрешенные комбинации»
ρ = t

Корректирующая способность
Число обнаруживаемых ошибок . Потребуем, чтобы сферы не захватывали соседние центры.
В этом случае центры шаров однозначно различимы, но при этом кодовое расстояние должно удовлетворять соотношению

Гарантированное число исправляемых ошибок
Возьмём кодовые вектора и образуем вокруг них сферы радиусом t и потребуем, чтобы эти сферы не пересекались, что гарантирует исправление ошибок.
Условия для требуемого кодового расстояния:

Обнаружение и исправление ошибок
Примеры.
1. Пусть n = 15, dmin = 5, то tиспр = 2 .
2. Если следует исправить 2 ошибки и обнаружить 4, то требуется dmin = 7 .
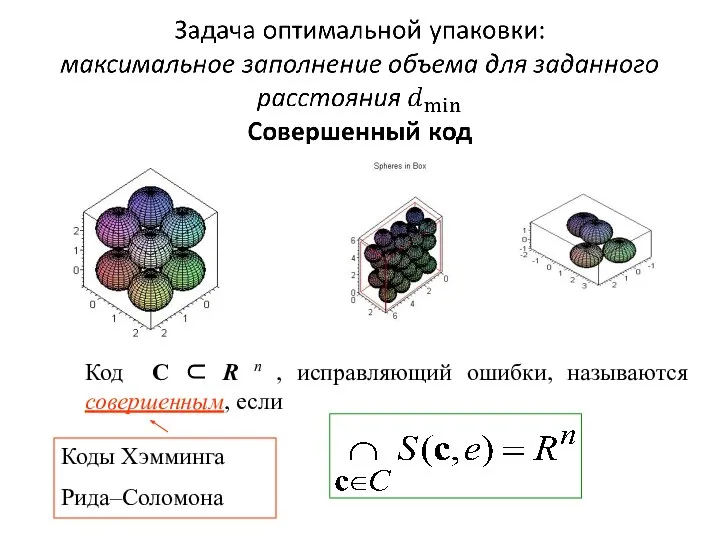
Это случай является композицией первых двух:

Код C ⊂ R n , исправляющий ошибки, называются совершенным, если
Коды Хэмминга
Рида–Соломона

Подход на основе теории графов
Код Хэмминга (7,4,3)
Граф Таннера
Несистемати-ческий
Системати-ческий

Алгебро-геометрический подход

Пример

Математика
Векторное пространство
Пусть V будет множеством векторов и F поле (множество) элементов называемых скалярами. V формирует векторное пространство над полем F если выполняются :
1. Закон коммутативности:
2.
3. Закон дистрибутивности:
4. Ассоциативность:
5.

Пространство и подпространство

Комбинаторные соотношения
Перестановка : (abc, acb, bac, bca, cba, cab)
n(n – 1)(n – 2)… 2⋅1 = n !
♥ число вариантов выбрать упорядоченный кортеж из k символов в множестве из n символов
n(n – 1)(n – 2)…(n – k + 2)(n – k + 1) = (n )k
♥ число вариантов выбрать неупорядоченный кортеж из k символов в множестве из n символов