Содержание
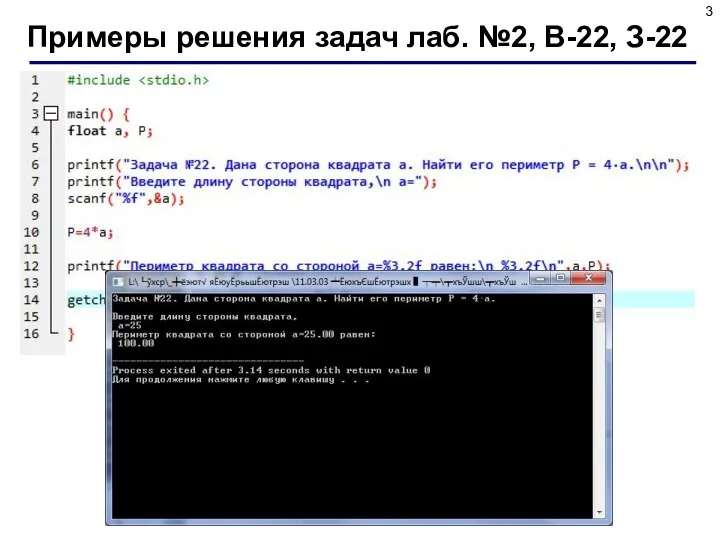
- 2. Задание Дана сторона квадрата a. Найти его периметр P = 4·a Алгоритм решения: Считываем значение стороны
- 3. Примеры решения задач лаб. №2, В-22, З-22
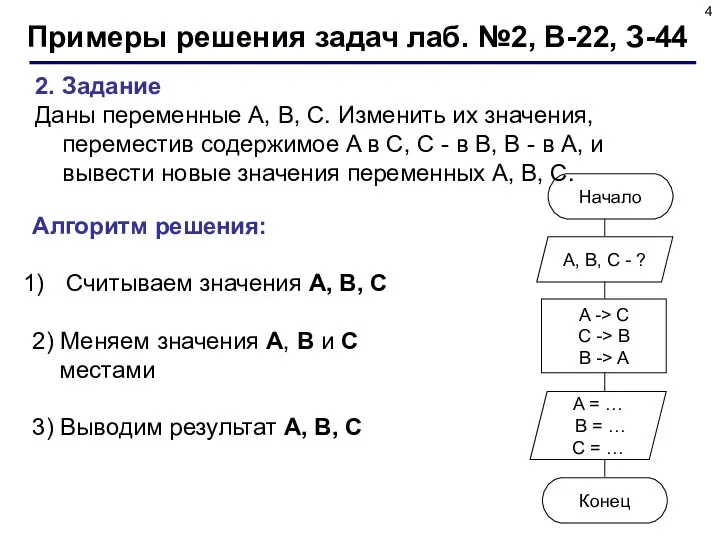
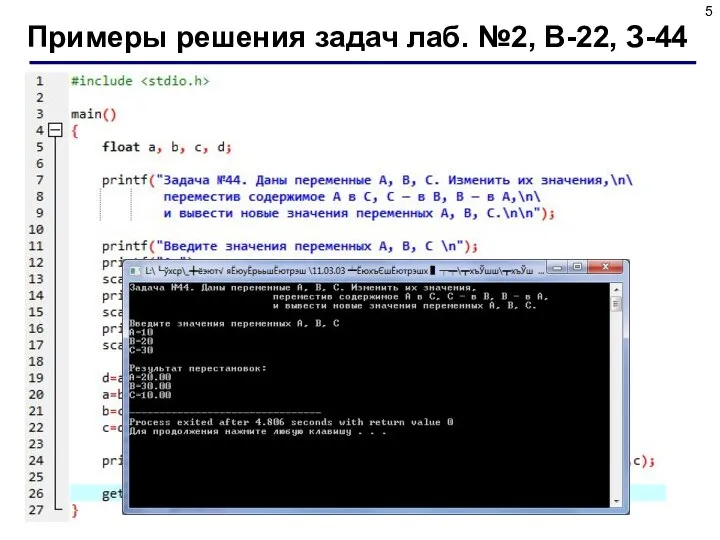
- 4. 2. Задание Даны переменные A, B, C. Изменить их значения, переместив содержимое A в C, C
- 5. Примеры решения задач лаб. №2, В-22, З-44
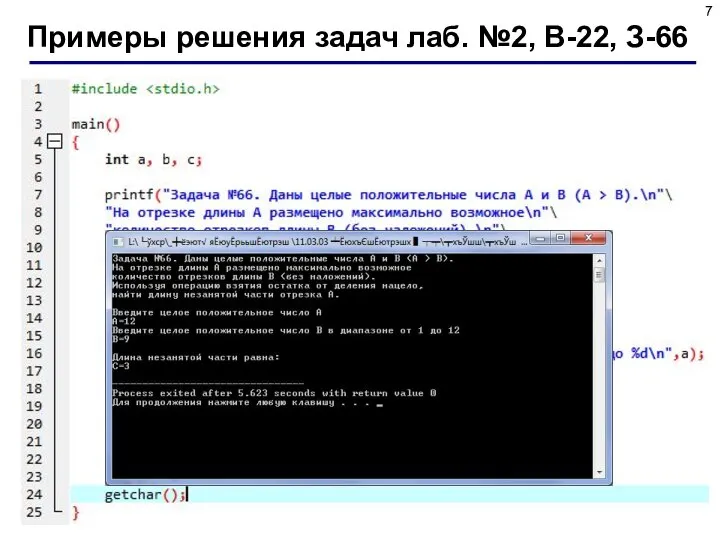
- 6. 3. Задание Даны целые положительные числа A и B (A > B). На отрезке длины A
- 7. Примеры решения задач лаб. №2, В-22, З-66
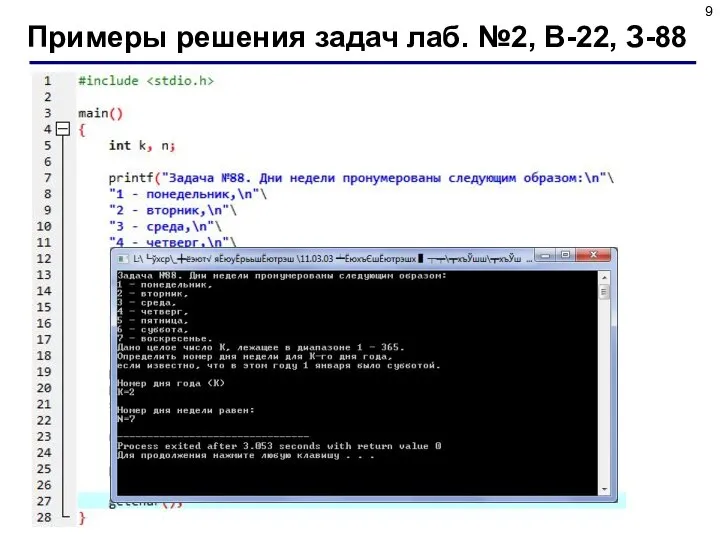
- 8. 4. Задание Дни недели пронумерованы следующим образом: 1 - понедельник, 2 - вторник, … , 6
- 9. Примеры решения задач лаб. №2, В-22, З-88
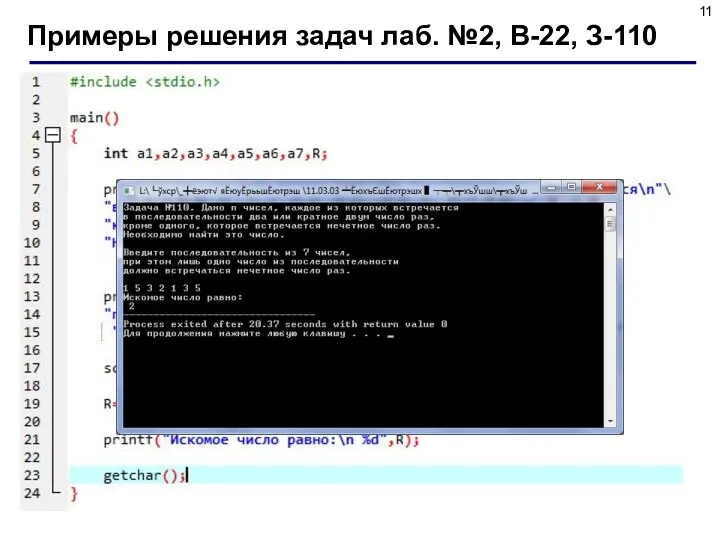
- 10. 5. Задание Дано n чисел, каждое из которых встречается в последовательности два или кратное двум число
- 11. Примеры решения задач лаб. №2, В-22, З-110
- 12. Основы программирования (на языке Си) Тема 8. Ветвления “разбор полетов”
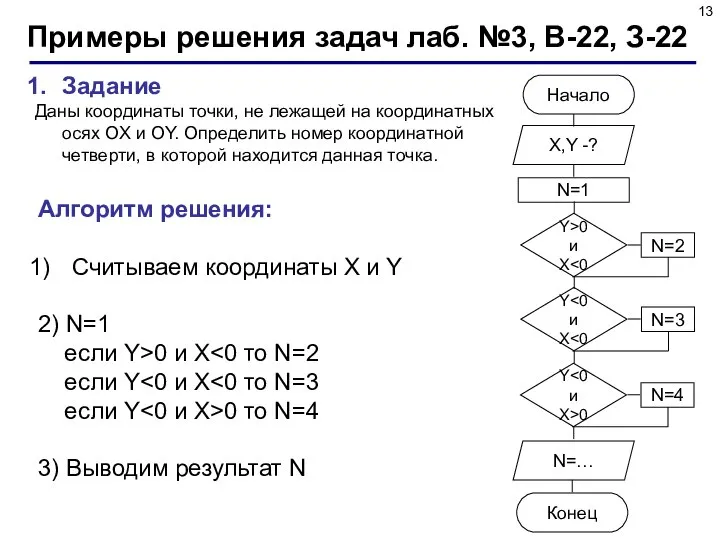
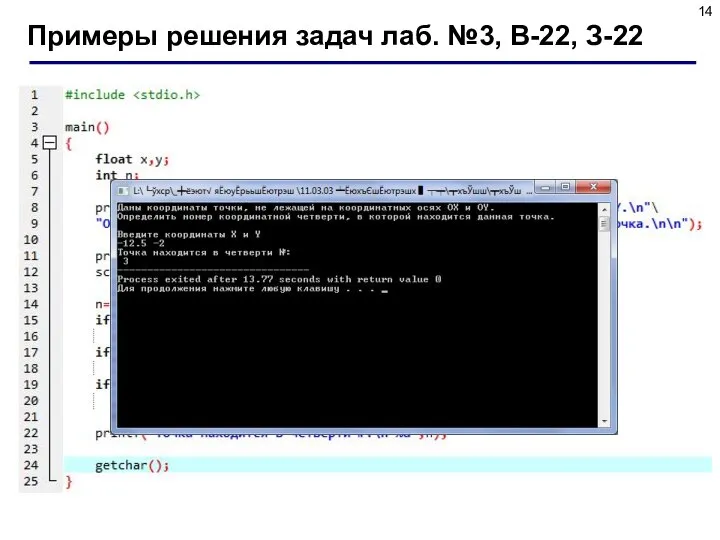
- 13. Задание Даны координаты точки, не лежащей на координатных осях OX и OY. Определить номер координатной четверти,
- 14. Примеры решения задач лаб. №3, В-22, З-22
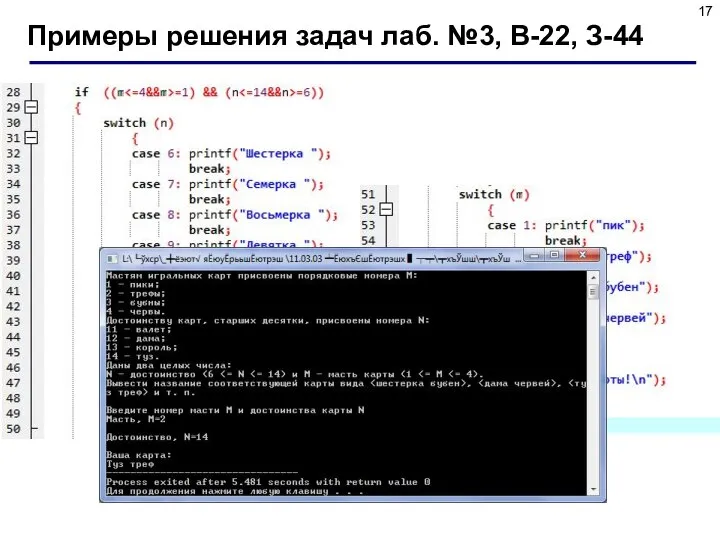
- 15. 2. Задание Мастям игральных карт присвоены порядковые номера: 1 - пики, 2 - трефы, 3 -
- 16. Примеры решения задач лаб. №3, В-22, З-44
- 17. Примеры решения задач лаб. №3, В-22, З-44
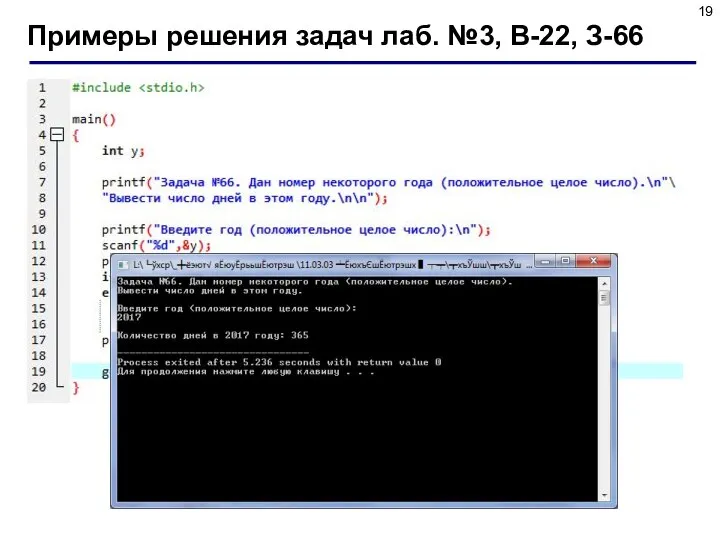
- 18. 3. Задание Дан номер некоторого года (положительное целое число). Вывести число дней в этом году, учитывая,
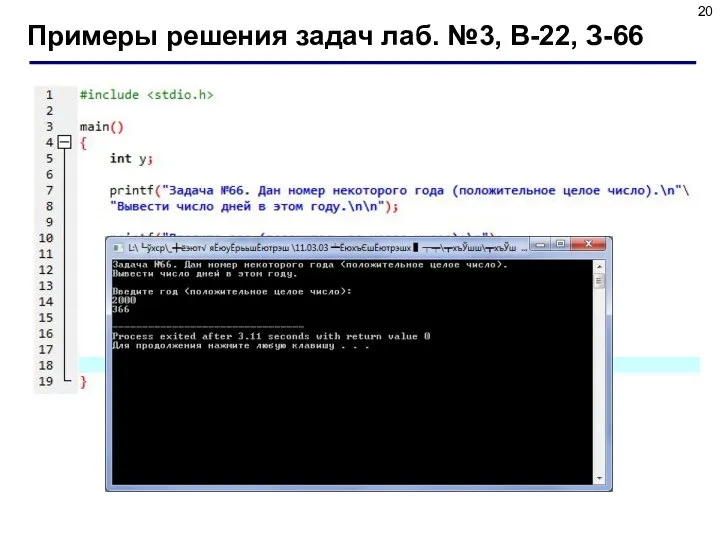
- 19. Примеры решения задач лаб. №3, В-22, З-66
- 20. Примеры решения задач лаб. №3, В-22, З-66
- 21. 4. Задание Даны три числа а, b, с. Определить, какое из них равно d. Если ни
- 22. Примеры решения задач лаб. №3, В-22, З-88
- 23. 5. Задание Сможет ли покупатель, располагающий суммой S рублей, приобрести a граммов конфет по цене b
- 25. Скачать презентацию











 Проектирование и создание профориентационного веб-узла
Проектирование и создание профориентационного веб-узла Розробка мобільного додатку ,що знаходить найвигідніші та найближчі магазини
Розробка мобільного додатку ,що знаходить найвигідніші та найближчі магазини События объекта TForm
События объекта TForm Источники пространственных данных. Их типы. Способы получения данных
Источники пространственных данных. Их типы. Способы получения данных Основные теоретические вопросы проектирования ПОР. Увеличение частоты дискретизации (Интерполяция) цифрового сигнала
Основные теоретические вопросы проектирования ПОР. Увеличение частоты дискретизации (Интерполяция) цифрового сигнала Программирование (АлгЯзык)
Программирование (АлгЯзык) Преобразование файлов из одного формата в другой
Преобразование файлов из одного формата в другой Аналитическая бизнес-справка на ЮЛ
Аналитическая бизнес-справка на ЮЛ Управление памятью
Управление памятью Организация работы локальной сети. Стек протоколов TCP/IP
Организация работы локальной сети. Стек протоколов TCP/IP Створення буклету на тему: Панель Інструментів в програмі InDisign
Створення буклету на тему: Панель Інструментів в програмі InDisign Ввод-вывод данных на консоль в С++
Ввод-вывод данных на консоль в С++ Информационная безопасность
Информационная безопасность Алгоритмическая конструкция ветвление. Основные алгоритмические конструкции
Алгоритмическая конструкция ветвление. Основные алгоритмические конструкции Google Планета Земля
Google Планета Земля 4eb6bf5c-266f-4f40-8f94-f85fa7e48a6c
4eb6bf5c-266f-4f40-8f94-f85fa7e48a6c Programación Orientada a Objetos
Programación Orientada a Objetos Все пути дерева
Все пути дерева Практика на телеканале ТюмГУ
Практика на телеканале ТюмГУ Історія та сучасність коректури
Історія та сучасність коректури Графические диктанты
Графические диктанты Прохождение учебно-производственной практики
Прохождение учебно-производственной практики Программа Sarafan
Программа Sarafan Технология OLE-Automation
Технология OLE-Automation Зависимость от социальных сетей
Зависимость от социальных сетей Презентация о презентациях
Презентация о презентациях Создание документов в Microsoft Word. Курсы
Создание документов в Microsoft Word. Курсы Исполнитель Водолей
Исполнитель Водолей