Линейные списки

Условие задачи
Используя структуру стека подсчитать значение арифметического выражения, записанного в префиксной записи при условии, что используются знаки операций +, –, *, / и операнды являются вещественными положительными числами. Во вводимой пользователем строке числа и знаки операций разделяются одним пробелом.
Замечание: Префиксной формой записи выражения a <знак операции> b называется запись, в которой знак операции размещен перед операндами
<знак операции> a b. Примеры:
a - b → – a b
a * b + c → + * a b c
a * (b + c) → * a + b c
a + b / c / d * e → + a * / / b c d e

Обязательные условия
Использовать линейный список типа «Стек» и операции «Извлечь элемент из стека», «Добавить элемент в стек», выполненные в виде отдельных процедур.
И для чего же тут «Стек»?

Очевидно, что « стек », при реализации данной задачи, может послужить нам только для одной цели! А именно, для хранения самих чисел (операндов), над которыми мы производим какие-либо из операций сложения, вычитания, умножения и деления ( + , - , * , / )
Но всё таки лучше проверить:
Может в «стек» знаки сложить? – бессмысленно, куда ж девать числа?
А что ещё можно туда положить? - Ровным счётом ничего, если только всю входную строку поэлементно, но это уже глупости.
Итак, со «стеком» определились, самое время пояснить АЛГОРИТМ
LIFO
last in — first out
1
2
3
4

АЛГОРИТМ решения задачи
Понимание чего-либо всегда лучше приходит на практике, поэтому я разберу алгоритм решения данной задачи на конкретном примере.
Пусть входной строкой будет запись, содержащая все возможные знаки операций (+ , - , * , / )
INPUT: - * / 15 - 7 + 1 1 3 + 2 + 1 1
Логично было бы для начала разобраться со ВВОДОМ

INPUT
Так как запись состоит не только из чисел, то будем считывать строкой, которую назовём PolishNotationStr (длинно, но информативно)
И для нашего примера данной строке будет присвоено значение:
PolishNotationStr = “- * / 15 - 7 + 1 1 3 + 2 + 1 1”
По условию числа и знаки отделены пробелом, а значит разобьём строку по пробелам, и занесём подстроки в массив типа string. Для разбиения я написал не сложную функцию под названием Split()
arrayPolishNatation = { “-”, “*”, “/”, “15”, “-”, “7”, “+”, “1”, “1”, “3”, “+”, “2”, “+”, “1”, “1” };

Создание «стека»
Ввод мы организовали, теперь у нас данные лежат в массиве, поэтому нам уже пора начать перекладывать числа в стек, ну а для этого, разумеется, нужно создать список, и я это сделал как-то так
То есть мы просто создаём глобальный список под именем stack, который содержит два поля:
double data; // Информационное поле
// Вещественное по условию
node *next; // Указатель на следующий элемент
// списка
Итак, почему же я сделал список глобальным? исключительно ради удобства работы с функциями, в том числе и Pop и Push (о них позже), с таким же успехом список можно было объявить список и в другой области программы, и передавать параметром

Pop() и Push()
Мы продвинулись, на шаг вперёд, создав stack, но по прежнему не можем положить в него элемент, ну соответственно и взять первый элемент мы тоже пока не можем.
Это нужно исправить! Например, написав, функции:
Pop() - извлечь верхний элемент из стека
Push( double x ) – добавить элемент в стек

Вычисление результата
Почти всё готово, и мы подошли к основной части, теперь у нас есть всё чтобы начать рассматривать само исходное выражение
Итак, так как наша исходная запись – префиксная, то мне показалось более удобным, идти по массиву с конца, почему?
♦ Во-первых, конечный элемент не может быть знаком, в то время, как первый элемент всегда какой-либо из знаков
♦ Во-вторых, можно лишний раз не обращать внимание на НЕКОММУТОТИВНОСТЬ деления и вычитания, так как изначально в стек пойдут соответственно, вычитаемое и делитель

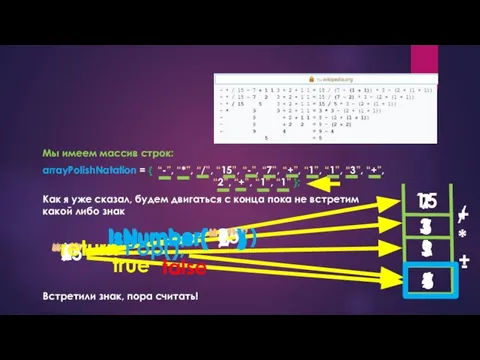
Мы имеем массив строк:
arrayPolishNatation = { “-”, “*”, “/”, “15”, “-”, “7”, “+”, “1”, “1”, “3”, “+”, “2”, “+”, “1”, “1” };
Как я уже сказал, будем двигаться с конца пока не встретим какой либо знак
Встретили знак, пора считать!
“1”
IsNumber(“1”)
true
1
1
IsNumber(“+”)
“+”
false
+
2
“2”
IsNumber(“2”)
2
“+”
IsNumber(“+”)
4
“3”
IsNumber(“3”)
3
“1”
IsNumber(“1”)
1
“1”
IsNumber(“1”)
1
“+”
IsNumber(“+”)
+
2
“7”
7
IsNumber(“7”)
“-”
IsNumber(“-”)
-
5
“15”
IsNumber(“15”)
15
“/”
IsNumber(“/”)
/
3
“*”
IsNumber(“*”)
*
9
“-”
IsNumber(“-”)
-
5
return Pop();