Содержание
- 2. ПОНЯТИЕ Понятие – форма мышления, фиксирующая основные, существенные признаки объекта Имеет две стороны: содержание и объем
- 3. ВЫСКАЗЫВАНИЕ на естественном языке на формальном языке «Два умножить на два равно четырем» «2*2=4». Высказывание -
- 4. Какие из предложений являются высказываниями? Определите их истинность. 1.Прослушайте сообщение. 2.Назовите устройство ввода информации. 3. Кто
- 5. УМОЗАКЛЮЧЕНИЕ Умозаключение - это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может
- 6. Алгебра в широком смысле этого слова – наука об общих операциях, аналогичных сложению и умножению, которые
- 7. А = «Два умножить на два равно четырем». В = «Два умножить на два равно пяти».
- 8. Для образования новых высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок «и»,
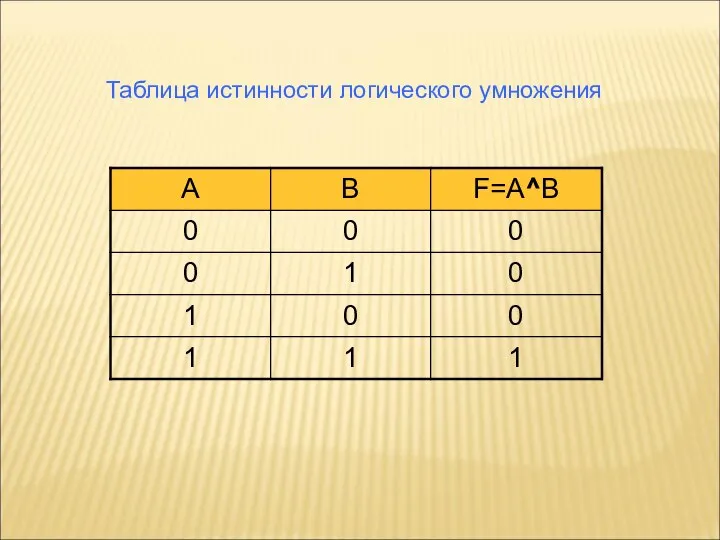
- 9. Логические умножение (конъюнкция) Объединение двух (или несколько) высказываний в одно с помощью союза «и» называются операцией
- 10. Обозначение логического умножения (конъюнкции) « &» либо «^». Образуем составное высказывание F, которое получится в результате
- 11. Таблица истинности логического умножения
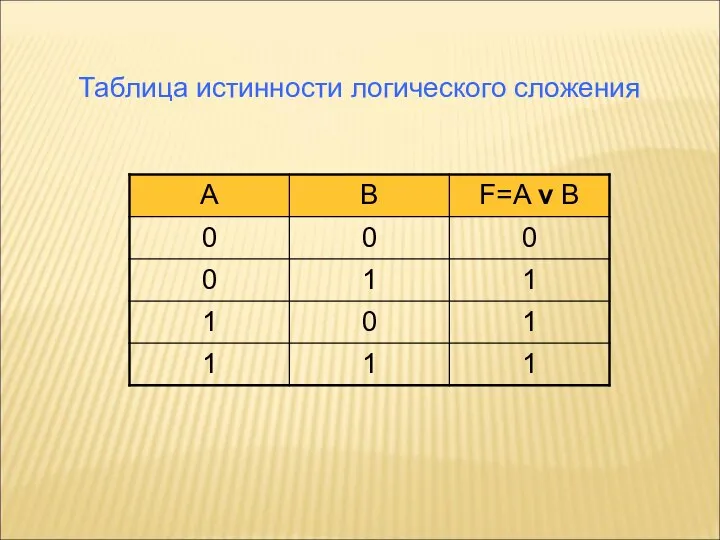
- 12. Логические сложения (дизъюнкция) Объединение двух (или нескольких) высказываний с помощью союза «или» называется операцией логического сложения
- 13. Обозначение логического сложения (дизъюнкции) «v» либо «+» Образуем составное высказывание F, которое получится в результате конъюнкции
- 14. Таблица истинности логического сложения
- 15. Логические отрицание (инверсия) Присоединение частицы «не» к высказываниям называются операцией логического отрицания или инверсией. Логическое отрицание
- 16. Обозначение логического отрицания (инверсии) А или ¬А Пусть А – истинное высказывание. Тогда высказывание F, образованное
- 17. Таблица истинности логического отрицания –
- 19. Скачать презентацию














 Алгоритмы. Алгоритм Эратросфена. Виды алгоритмов
Алгоритмы. Алгоритм Эратросфена. Виды алгоритмов Лямбда-архитектура
Лямбда-архитектура Деревья решений
Деревья решений Информационные модели: системы и структуры данных
Информационные модели: системы и структуры данных Инструменты графического редактора Paint
Инструменты графического редактора Paint Устранение цифрового неравенства в Матвеевском районе
Устранение цифрового неравенства в Матвеевском районе Особенности современных ЭВМ
Особенности современных ЭВМ Pascal ABC. Работа с числовыми данными. Целые числа. Урок 3-4
Pascal ABC. Работа с числовыми данными. Целые числа. Урок 3-4 Электронное портфолио школьника. Участвуй-заполняй-побеждай
Электронное портфолио школьника. Участвуй-заполняй-побеждай Университетская газета Молодость
Университетская газета Молодость Словесные информационные модели
Словесные информационные модели Адресация в интернете
Адресация в интернете Мобильные приложения как средство изучения иностранного языка
Мобильные приложения как средство изучения иностранного языка MSE block library for Simulink
MSE block library for Simulink DIDO Wi Fi (Distributed Input Distributed Output)
DIDO Wi Fi (Distributed Input Distributed Output) Искусственный интеллект
Искусственный интеллект Работа с таблицами (10 класс)
Работа с таблицами (10 класс) Множества
Множества Обзор интернет-ресурсов, программ и приложений по созданию интерактивных пособий, презентаций и дидактических игр
Обзор интернет-ресурсов, программ и приложений по созданию интерактивных пособий, презентаций и дидактических игр Технологии и опыт мирового уровня в области системной интеграции и разработки программного обеспечения
Технологии и опыт мирового уровня в области системной интеграции и разработки программного обеспечения Получение сведений из фонда данных государственной кадастровой оценки
Получение сведений из фонда данных государственной кадастровой оценки Электронная система расписания
Электронная система расписания Практика в газете Пермский университет
Практика в газете Пермский университет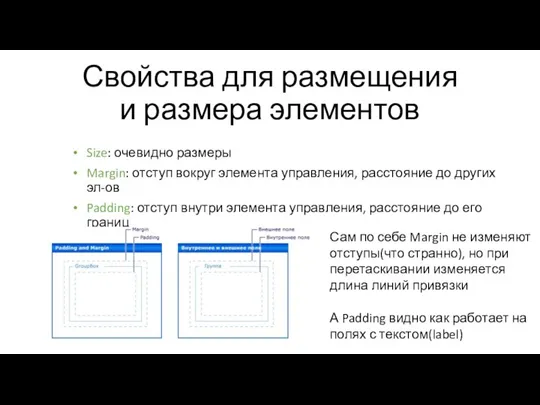 Свойства для размещения и размера элементов
Свойства для размещения и размера элементов Мобильная служба организации краткосрочных событий
Мобильная служба организации краткосрочных событий Школа программирования
Школа программирования Знакомство с новой лексикой
Знакомство с новой лексикой Рекламный интернет-проект ШУМ
Рекламный интернет-проект ШУМ