Содержание
- 2. 2.1. Что нужно знать для управления? Цель любого управления – изменить состояние объекта нужным образом (в
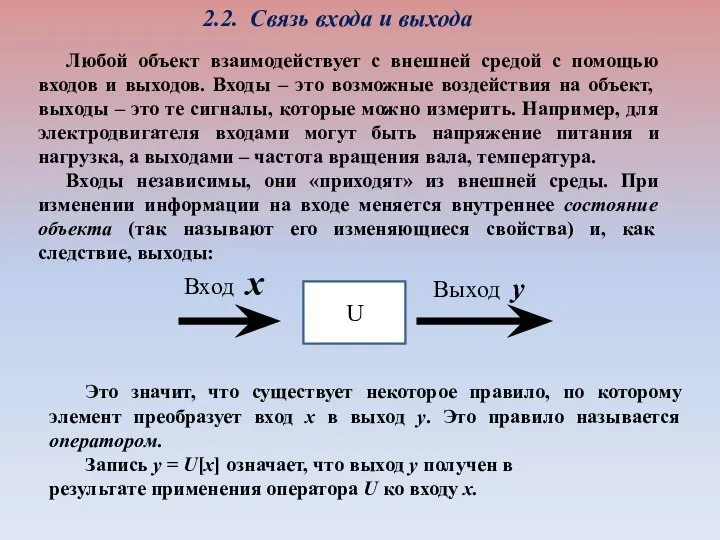
- 3. 2.2. Связь входа и выхода Любой объект взаимодействует с внешней средой с помощью входов и выходов.
- 4. Построить модель – это значит найти оператор, связывающий входы и выходы. С его помощью можно предсказать
- 5. Очевидно, что нет, потому что полученная зависимость справедлива только для постоянного входного сигнала. Если напряжение на
- 6. Обратный оператор – оператор дифференцирования – вычисляет производную: Данный оператор играет очень важную роль в описании
- 7. Где встречаются такие операторы? Приведем примеры из электротехники. Например, известно, что ток i ( в амперах),
- 8. Оператор дифференцирования – это идеальный (физически нереализуемый) оператор, его невозможно реализовать на практике. Чтобы понять это
- 9. 2.3. Как строятся модели? Во-первых, математические модели могут быть получены теоретически из законов физики (законы сохранения
- 10. Первое уравнение означает, что разность потенциалов на концах RLC-цепочки равна сумме разностей потенциалов на всех промежуточных
- 11. На практике часто используется смешанный способ: структура модели (вид уравнения, связывающего вход и выход) определяется из
- 12. С другой стороны, можно упростить модель объекта, отбросив некоторые «детали», которые кажутся разработчику маловажными. Для упрощенной
- 13. 2.4. Линейность и нелинейность Из школьной математики известно, что проще всего решать линейные уравнения. С нелинейными
- 14. Однако, все модели реальных систем – нелинейные. Это легко понять хотя бы потому, что всегда есть
- 15. Нужно отметить, что если объект или привод имеют так называемую «существенную» не-линейность, этот подход может не
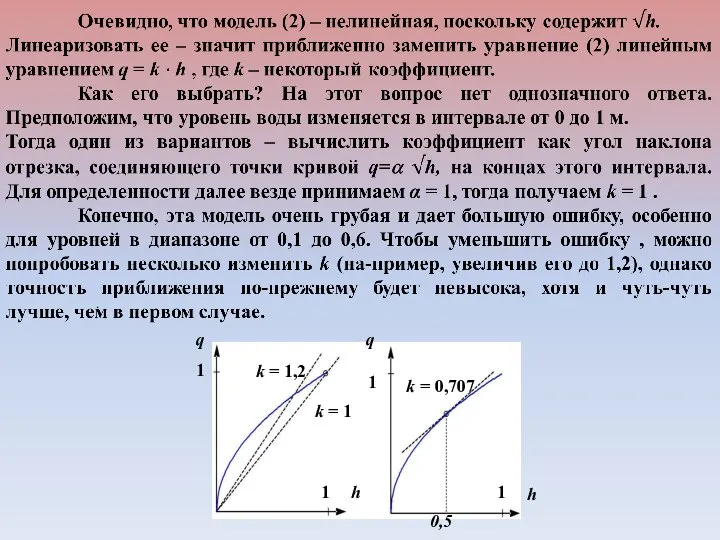
- 16. 2.5. Линеаризация уравнений Мы уже отметили, что в теории управления лучше всего разработаны методы исследования линейных
- 17. 2.5.1 Алгебраические уравнения h S q
- 18. . q q h h 1 1 1 1 k = 1 k = 1,2 k
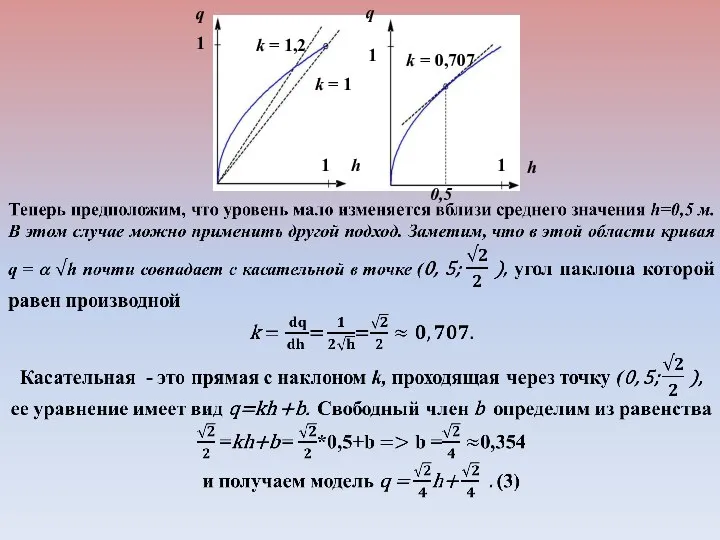
- 19. q q h h 1 1 1 1 k = 1 k = 1,2 k =
- 21. 2.5.2 Дифференциальные уравнения Реальные объекты не могут мгновенно изменять свое состояние, поэтому вместо статических моделей типа
- 24. Дальше для линеаризации используется разложение функций в ряд Тейлора. Для некоторой функции f (x, y) в
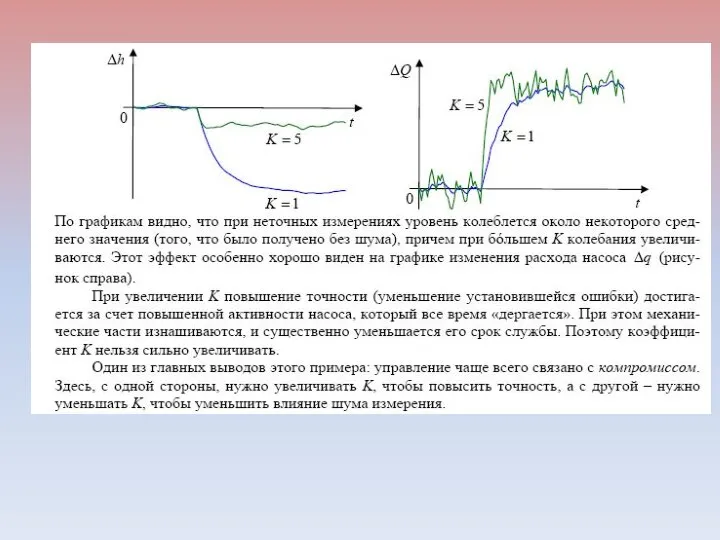
- 26. 2.6. Управление Посмотрим на примере, как можно управлять объектом и что из этого получается. Немного изменим
- 27. Построим математическую модель объекта, то есть цистерны. Поток на выходе показывает, сколько воды вытекает из цистерны
- 32. Скачать презентацию

























 Вопросы Маркизза Нетикета. Викторина для учащихся младшего и среднего школьного возраста
Вопросы Маркизза Нетикета. Викторина для учащихся младшего и среднего школьного возраста История развития компьютерной техники
История развития компьютерной техники Ремонт и обслуживание системы охлаждения в персональном компьютере
Ремонт и обслуживание системы охлаждения в персональном компьютере Компьютерная графика
Компьютерная графика Основы командной работы
Основы командной работы Линейный массив
Линейный массив Презентація на тему : « ОРНАМЕНТИ ТА ВИДИ ОРНАМЕНТІВ. СИМВОЛИ В УКРАЇНСЬКІЙ НАРОДНІЙ ВИШИВЦІ » Роботу виконала Андріянова Аліна
Презентація на тему : « ОРНАМЕНТИ ТА ВИДИ ОРНАМЕНТІВ. СИМВОЛИ В УКРАЇНСЬКІЙ НАРОДНІЙ ВИШИВЦІ » Роботу виконала Андріянова Аліна Презентация на тему Начните работу с нажатия кнопки Пуск
Презентация на тему Начните работу с нажатия кнопки Пуск  Основы Web-программирования
Основы Web-программирования Контроль и защита информации в автоматизированных системах
Контроль и защита информации в автоматизированных системах Создание DLL, работа с базой данных. Лекция 9
Создание DLL, работа с базой данных. Лекция 9 диаграммы в Excel
диаграммы в Excel Операционные системы и среды. Понятие файл, каталог, файловая система
Операционные системы и среды. Понятие файл, каталог, файловая система Массива. Одномерные массивы
Массива. Одномерные массивы Просвещенный абсолютизм
Просвещенный абсолютизм Идентификация и определение научных коллективов
Идентификация и определение научных коллективов Процесс исполнения входящего документа ОСЭД
Процесс исполнения входящего документа ОСЭД Прикладное ПО. Системное ПО. Системы программирования
Прикладное ПО. Системное ПО. Системы программирования PSP mobile app description
PSP mobile app description Алгоритмы и исполнители
Алгоритмы и исполнители Понятие операционной системы
Понятие операционной системы Команда “Tamagochi”
Команда “Tamagochi” Почта Росии
Почта Росии Информатика в нашей жизни
Информатика в нашей жизни Разработка автоматизированной информационной системы для ИТ-службы
Разработка автоматизированной информационной системы для ИТ-службы Описание клинического случая
Описание клинического случая Арифметические основы организации ЭВМ
Арифметические основы организации ЭВМ Модификация системы защиты информации выделенного помещения рекрутингового агентства
Модификация системы защиты информации выделенного помещения рекрутингового агентства