Компьютерное информационное моделирование

Задания для самостоятельного решения
Этапы моделирования
Материальные и информационные модели
Структуры данных
Понятие модели
Используемые материалы

Задания для самостоятельного решения
Этапы моделирования
Материальные и информационные модели
Структуры данных
Понятие модели
Используемые материалы

Задания для самостоятельного решения
Этапы моделирования
Материальные и информационные модели
Структуры данных
Понятие модели
Используемые материалы

Задания для самостоятельного решения
Этапы моделирования
Материальные и информационные модели
Структуры данных
Понятие модели
Используемые материалы

Задания для самостоятельного решения
Этапы моделирования
Материальные и информационные модели
Структуры данных
Понятие модели
графы
деревья
таблицы
Используемые материалы

Задания для самостоятельного решения
Этапы моделирования
Материальные и информационные модели
Структуры данных
Понятие модели
графы
деревья
таблицы
Используемые материалы

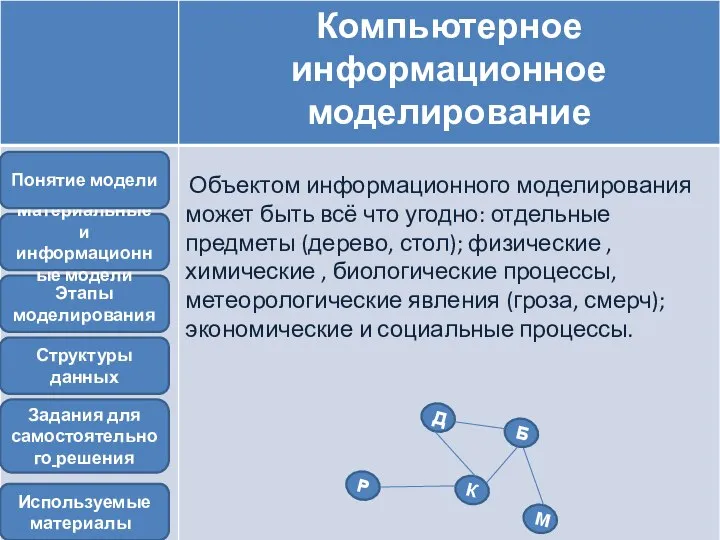
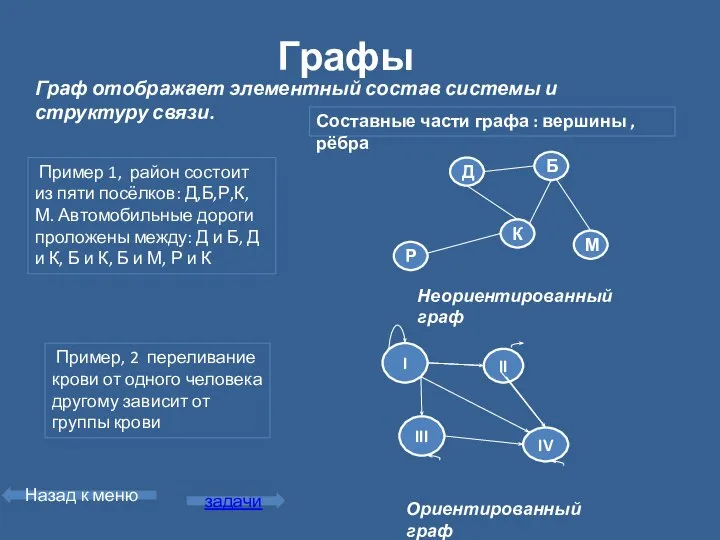
Графы
Пример 1, район состоит из пяти посёлков: Д,Б,Р,К, М. Автомобильные дороги проложены между: Д и Б, Д и К, Б и К, Б и М, Р и К
Неориентированный граф
Граф отображает элементный состав системы и структуру связи.
Ориентированный граф
Пример, 2 переливание крови от одного человека другому зависит от группы крови
Составные части графа : вершины , рёбра
задачи
Назад к меню

Изобразите в виде графа систему, состоящую из четырех одногруппников, между которыми существуют следующие связи (взаимоотношения): дружат: Саша и Маша, Саша и Даша, Маша и Гриша, Гриша и Саша. Глядя на полученный граф, ответьте на вопрос: с кем Саша может поделиться секретом, не рискуя, что он станет известен кому-то другому?
Нарисовать ориентированный граф (блок-схему) проверки преподавателем тетрадей. В систему команд входят команды : проверить работу; взять тетрадь из пачки; выставить оценку; выяснить, остались ли ещё не проверенные тетради.
Нарисуйте два варианта графа системы «Компьютер», содержащего следующие вершины: процессор, оперативная память, внешняя память, клавиатура, монитор, принтер; а) линия связи обозначает отношение «передает информацию»; б) линия связи обозначает отношение «управляет».
Нарисуйте блок-схему поиска фальшивой монеты среди 10 монет. Имеем чашечные весы и известно, что фальшивая монета всего одна , и она легче настоящих.
Задания
Назад к меню

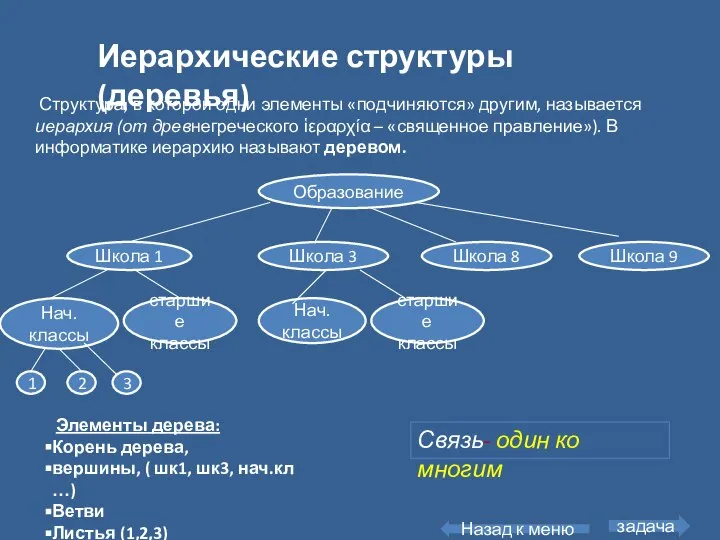
Иерархические структуры (деревья)
Элементы дерева:
Корень дерева,
вершины, ( шк1, шк3, нач.кл …)
Ветви
Листья (1,2,3)
Связь- один ко многим
Структура, в которой одни элементы «подчиняются» другим, называется иерархия (от древнегреческого ἱεραρχία – «священное правление»). В информатике иерархию называют деревом.
задача
Назад к меню

Постройте граф структуры управления вашим колледжом. Оказался ли он деревом? Если да, то что находится в корне этого дерева? Что является листьями?
Задания
Назад к меню

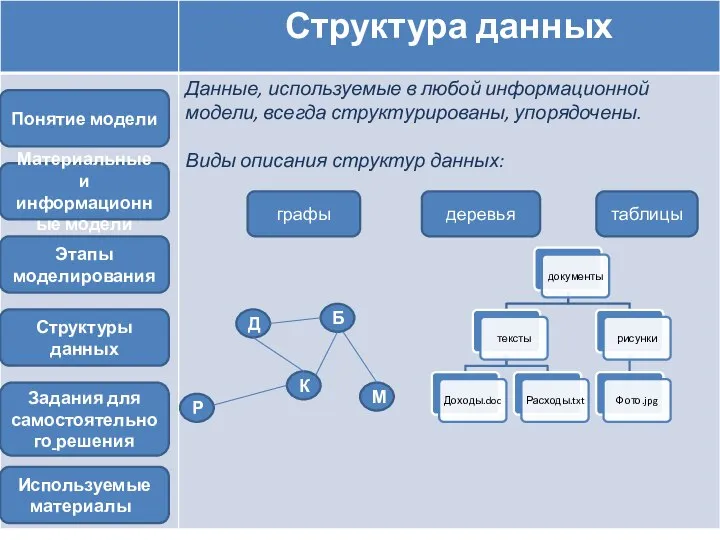
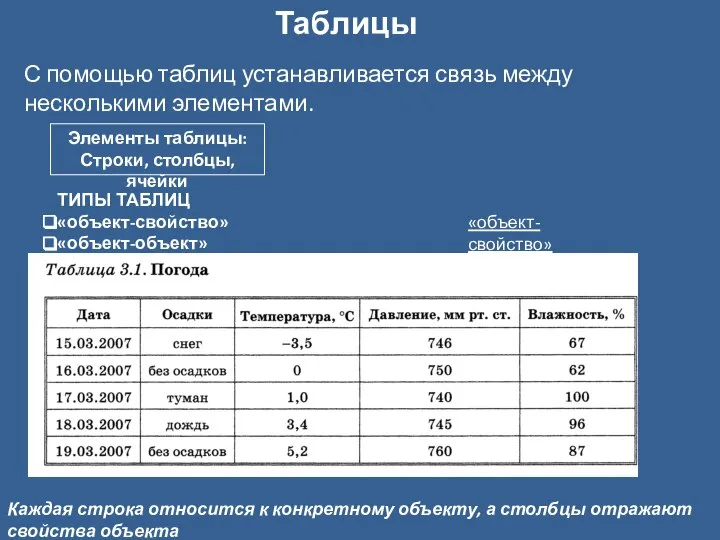
Таблицы
Элементы таблицы:
Строки, столбцы, ячейки
ТИПЫ ТАБЛИЦ
«объект-свойство»
«объект-объект»
«объект-свойство»
С помощью таблиц устанавливается связь между несколькими элементами.
Каждая строка относится к конкретному объекту, а столбцы отражают свойства объекта

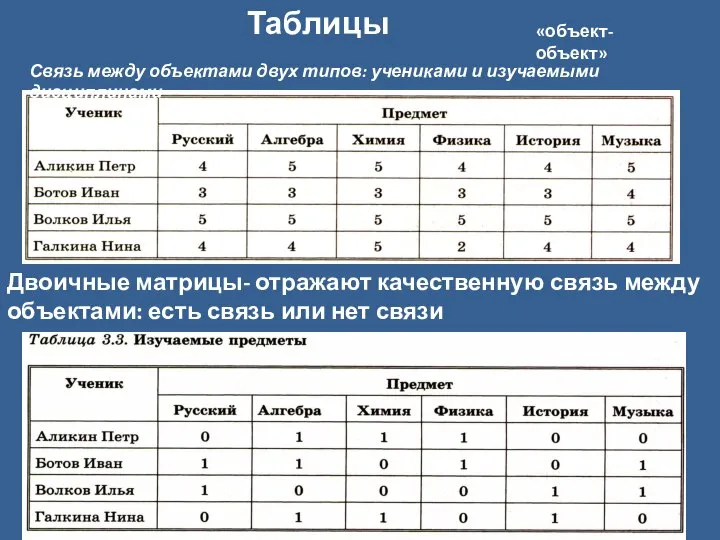
«объект-объект»
Таблицы
Связь между объектами двух типов: учениками и изучаемыми дисциплинами
Двоичные матрицы- отражают качественную связь между объектами: есть связь или нет связи

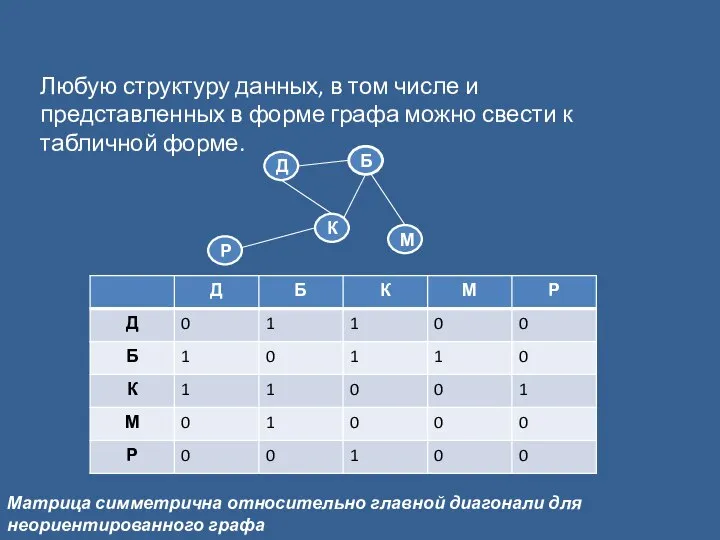
Любую структуру данных, в том числе и представленных в форме графа можно свести к табличной форме.
Матрица симметрична относительно главной диагонали для неориентированного графа

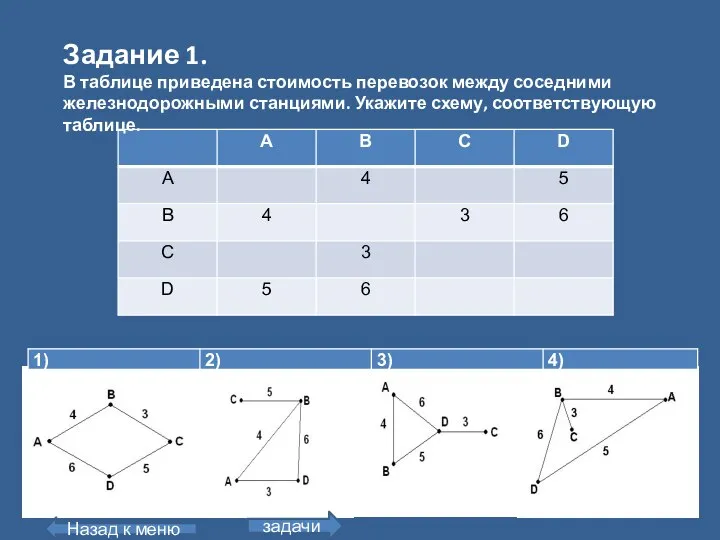
Задание 1.
В таблице приведена стоимость перевозок между соседними железнодорожными станциями. Укажите схему, соответствующую таблице.
Назад к меню
задачи

Двоичные матрицы удобно использовать для решения некоторых логических задач — головоломок. Попробуйте таким путем решить следующие задачи.
Имена Иванова, Петрова, Семенова и Николаева — Иван, Петр, Семен и Николай, причем только у Николаева имя совпадает с фамилией, т. е. его зовут Николай. Семенова зовут не Петром. Определить фамилию и имя каждого человека.
В Норильске, Москве, Ростове и Пятигорске живут четыре супружеские пары, причем в каждом городе — только одна пара. Имена этих супругов: Антон, Борис, Давид, Григорий, Ольга, Мария, Светлана, Екатерина. Антон живет в Норильске, Борис и Ольга — супруги, Григорий и Светлана не живут в одном городе, Мария живет в Москве, Светлана — ростовчанка. Кто на ком женат и кто где живет?
Задания
К решению
Назад к меню
К следующей задаче

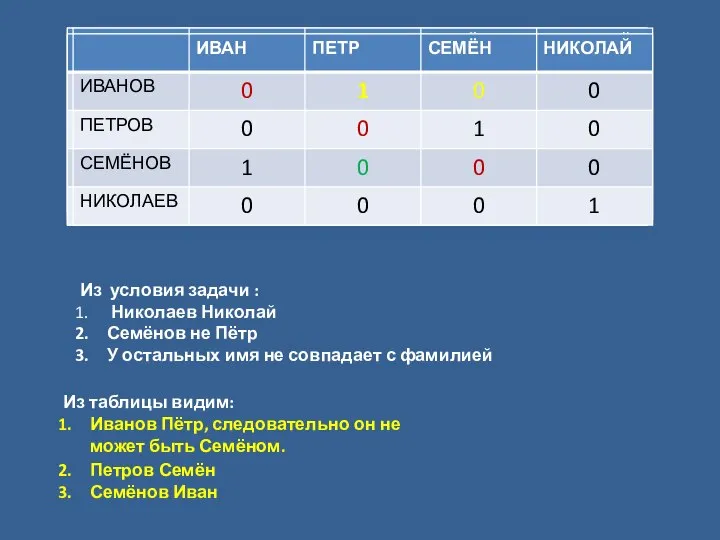
Задания
В колледже учатся четыре талантливых мальчика: Иванов, Петров, Сидоров и Андреев. Один из них — будущий музыкант, другой преуспел в бальных танцах, третий — солист хора мальчиков, четвертый подает надежды как художник.
О них известно следующее:
Иванов и Сидоров присутствовали в зале консерватории, когда там солировал в хоре мальчиков певец.
Петров и музыкант вместе позировали художнику.
Музыкант раньше дружил с Андреевым, а теперь хочет позна­комиться с Ивановым.
Иванов не знаком с Сидоровым, так как они учатся в разных классах и в разные смены.
Кто чем увлекается?
Назад к меню
К решению

Из условия задачи :
Николаев Николай
Семёнов не Пётр
У остальных имя не совпадает с фамилией
Из таблицы видим:
Иванов Пётр, следовательно он не может быть Семёном.
Петров Семён
Семёнов Иван

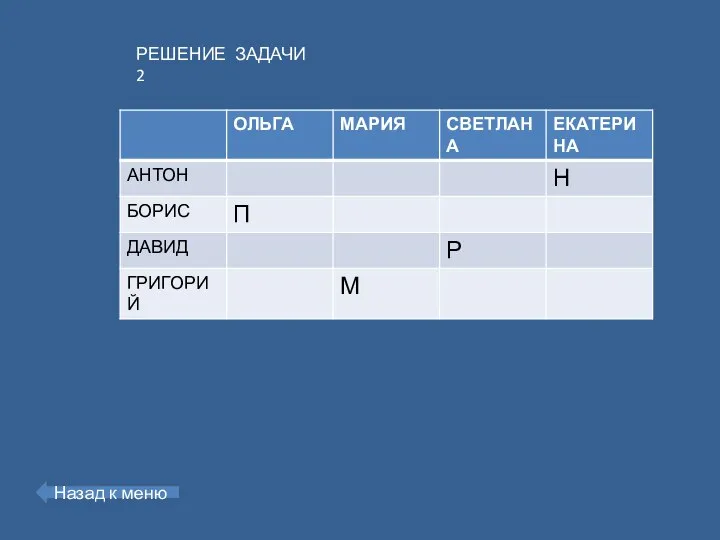
РЕШЕНИЕ ЗАДАЧИ 2
Назад к меню

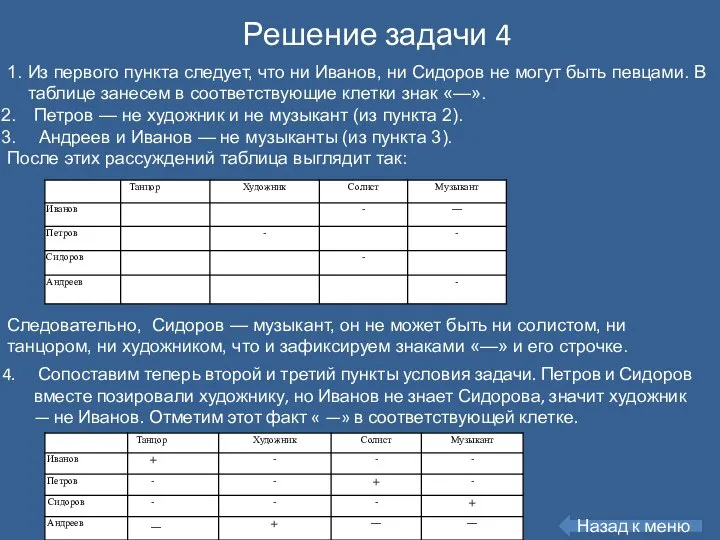
Решение задачи 4
1. Из первого пункта следует, что ни Иванов, ни Сидоров не могут быть певцами. В таблице занесем в соответствующие клетки знак «—».
Петров — не художник и не музыкант (из пункта 2).
Андреев и Иванов — не музыканты (из пункта 3).
После этих рассуждений таблица выглядит так:
Следовательно, Сидоров — музыкант, он не может быть ни солистом, ни танцором, ни художником, что и зафиксируем знаками «—» и его строчке.
Сопоставим теперь второй и третий пункты условия задачи. Петров и Сидоров вместе позировали художнику, но Иванов не знает Сидорова, значит художник — не Иванов. Отметим этот факт « —» в соответствующей клетке.
Назад к меню