Слайд 2Актуальность
Проблема высокой генетической изменчивости ВИЧ.
Необходимость в улучшении эффективности противовирусной терапии и в

разработке оптимальных стратегий лечения.
Необходимость понять закономерности развития популяции вируса в организме человека.
Слайд 3Цели
Изучение разных подходов к построению моделей вирусной динамики
Построение стохастической и дифференциальной моделей

динамики квазивидов ВИЧ, учитывающей действия протекающих в популяции вируса процессов.
Анализ воздействия применения противовирусного препарата на вирусную динамику
Слайд 4Стохастическая модель
Четырехбуквенный алфавит, каждая буква соответствует нуклеотиду
Виртуальный геном (строка длины 1800)
Квазитипы (всего

8, определяются 121-123 и 643-645 позициями)
Популяция (массив геномов, количество остается постоянным)
Слайд 5 Были изучены принципы работы генетических алгоритмов, которые включают в себя процессы:
рекомбинации
мутации
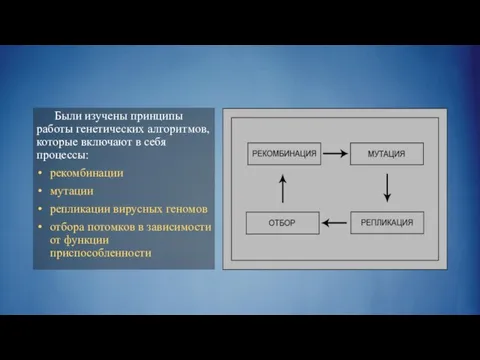
репликации вирусных геномов
отбора потомков в зависимости от функции приспособленности
Слайд 6Рекомбинация
Вероятность рекомбинации: 0.5

Слайд 7Вероятность мутации: 0.2
Мутация

Слайд 8Репликация
Реализована как умножение количества генов всех типов на число (20)

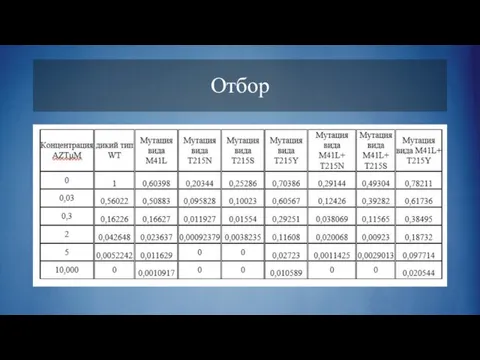
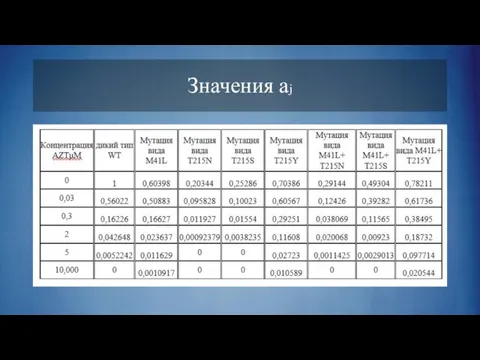
Слайд 10 Написана программа в MATLAB, проведены расчеты с параметрами:
Размер популяции – 1000
Длина генома

– 1800
Вероятность точечной мутации – 0,2
Вероятность рекомбинации – 0,5
Количество поколений – 1000
Результаты приведены в виде графиков, демонстрирующих количественное соотношение частиц рассмотренных квазитипов в популяции для разных значений концентрации AZTμM
Слайд 11Результаты работы программы для AZTμM = 0
Количество вирусных частиц рассмотренных квазитипов при
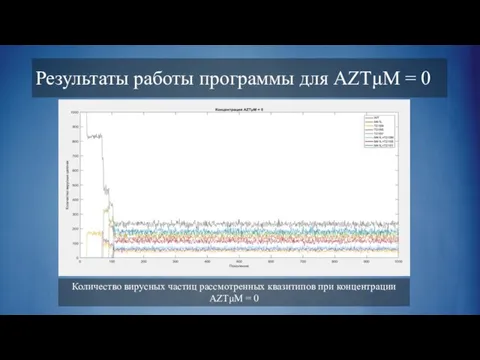
концентрации AZTμM = 0
Слайд 12Количество вирусных частиц рассмотренных квазитипов при концентрации AZTμM = 0,3
Результаты работы программы
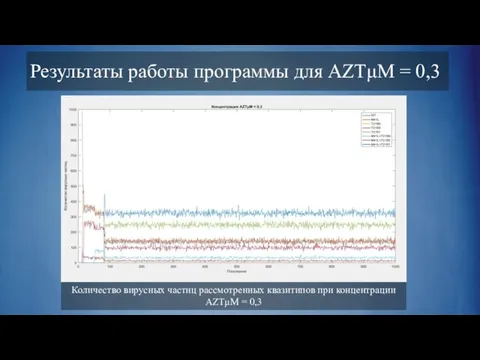
для AZTμM = 0,3
Слайд 13Результаты работы программы для AZTμM = 0
Усредненное количество вирусных частиц рассмотренных квазитипов
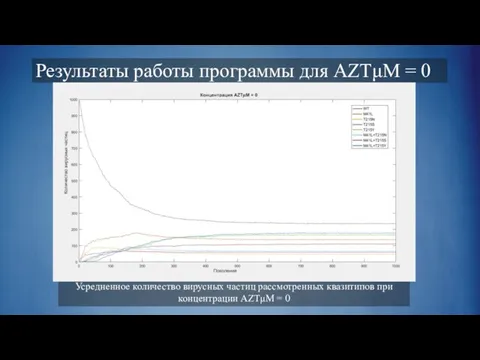
при концентрации AZTμM = 0
Слайд 14Результаты работы программы для AZTμM = 0,3
Усредненное количество вирусных частиц рассмотренных квазитипов
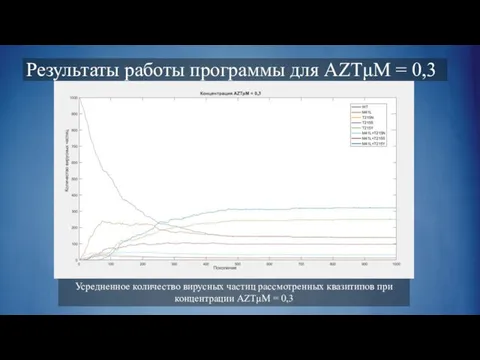
при концентрации AZTμM = 0,3
Слайд 15Анализ степени генетического разнообразия
Определяется как число позиций, в которых соответствующие символы двух

строк A и B одинаковой длины различны.
Слайд 16Алгоритм
Сравним все первые гены цепочек во всей популяции, просуммируем количества разных нуклеотидов
Затем

по формуле числа сочетаний из N по 2 посчитаем количество пар геномов с одинаковыми нуклеотидами
Сложим
Вычтем из общего количества возможных пар геномов
Получим количество пар геномов с различными нуклеотидами в паре для первой позиции в геноме.
Повторим для остальных позиций, просуммируем. Разделим на количество пар геномов в популяции. Получим среднее расстояние Хэмминга на популяцию.
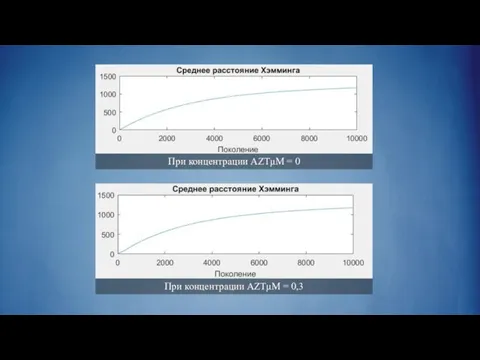
Слайд 17При концентрации AZTμM = 0
При концентрации AZTμM = 0,3
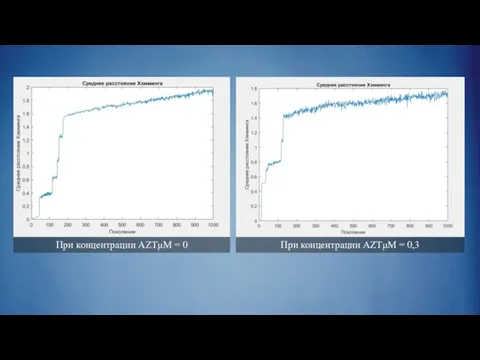
Слайд 18При концентрации AZTμM = 0
При концентрации AZTμM = 0,3
Слайд 19Дифференциальная модель
Если численность популяции велика, эволюция может рассматриваться как детерминированный процесс.
В

этом случае эволюционная динамика популяции может быть описана системой обыкновенных дифференциальных уравнений (ОДУ).
Решением системы будут функции, описывающие динамику численности квазивидов в популяции с течением времени
Слайд 20Предположим, что существует n различных разновидностей нуклеиновых кислот v1,…,vn, каждая характеризуется определенной

последовательностью нуклеотидов, которая определяет скорость репликации данной разновидности.
Скорости репликации A1,…,An
Qij – вероятности того, что при репликации цепочка вида vj в результате мутации станет цепочкой вида vi
Слайд 22Примеры начальных условий
(1)
(2)

Слайд 24Можно считать, что:
Вероятность замены одного основания на другое в конкретной позиции: p

= 2*10^-5
Вероятность того, что ни в одной из позиций (121-123 или 643-645) ни одно из кодирующих оснований не изменится:
Qii = (1-3p)^6
Вероятность конкретной мутации в одном из шести рассматриваемых оснований: Qij = p(1-3p)^5
Если для перехода от одного мутанта к другому необходимо более двух мутаций, считается, что вероятность такого перехода равна нулю
Слайд 26Если считать концентрацию противовирусного препарата в организме пациента постоянной, система является системой

ОДУ с постоянными коэффициентами.
Для исследования динамики популяции следует задать начальные условия – размеры субпопуляций (численности каждого квазивида) до начала терапии.
Для численного решения системы уравнений использовался алгоритм ode15s для решения жёстких систем ОДУ, реализованный в пакете MATLAB.
Слайд 27При концентрации AZTμM = 0, начальные условия (1) (однородная популяция в начальный
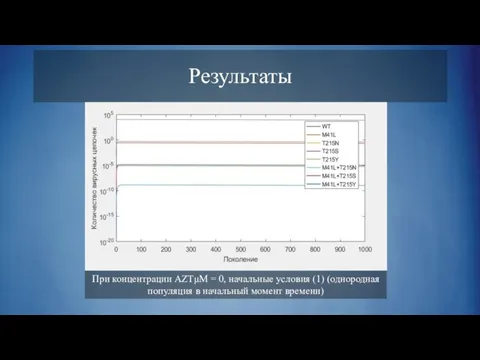
момент времени)
Результаты
Слайд 28При концентрации AZTμM = 0, начальные условия (2) (равномерное распределение квазитипов в
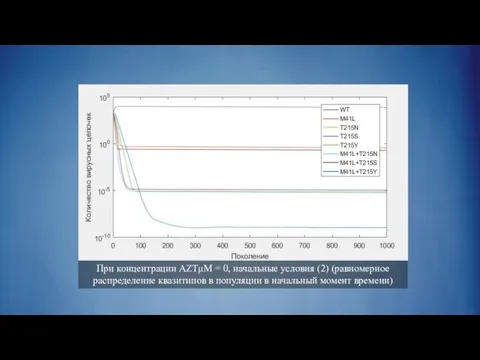
популяции в начальный момент времени)
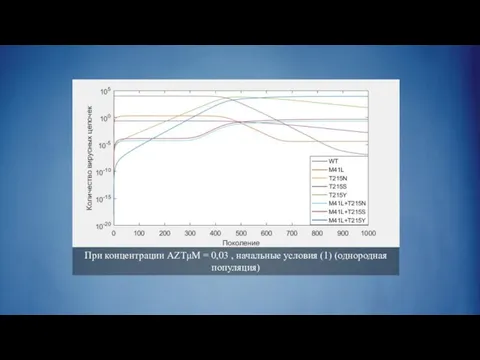
Слайд 29При концентрации AZTμM = 0,03 , начальные условия (1) (однородная популяция)
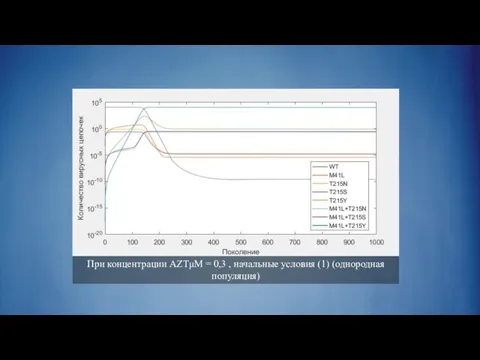
Слайд 30При концентрации AZTμM = 0,3 , начальные условия (1) (однородная популяция)
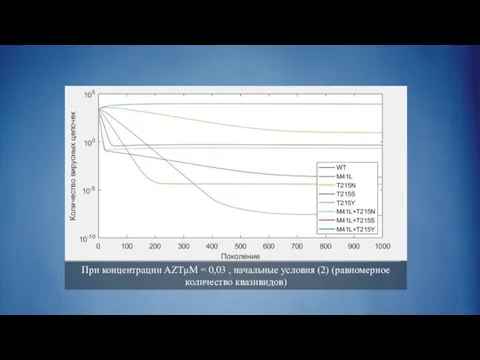
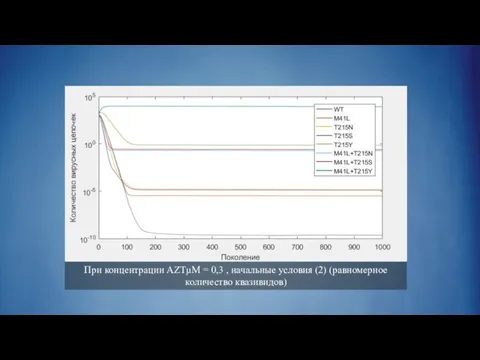
Слайд 31При концентрации AZTμM = 0,03 , начальные условия (2) (равномерное количество квазивидов)
Слайд 32При концентрации AZTμM = 0,3 , начальные условия (2) (равномерное количество квазивидов)
Слайд 33Результаты
Результаты построения моделей показывают, что в процессе воспроизводства популяция по-прежнему остается неоднородной,

но соотношение численности составляющих ее квазивидов существенно изменяется в зависимости от условий – концентрации противовирусного препарата, то есть зависят от значений функции приспособленности.
Слайд 34Графический интерфейс
В состав MatLab входит среда GUIDE для создания приложений с графическим
интерфейсом пользователя.































 Программирование на языке Паскаль. Циклы с условием
Программирование на языке Паскаль. Циклы с условием CloudTips для блогеров, стримеров, подкастеров, музыкантов и артистов чаевые и донаты на любую карту моментально
CloudTips для блогеров, стримеров, подкастеров, музыкантов и артистов чаевые и донаты на любую карту моментально Текстовые документы и технологии их создания. Обработка текстовой информации
Текстовые документы и технологии их создания. Обработка текстовой информации Информатика
Информатика Создание многоуровневого списка Учитель информатики МАОУ "СОШ №55" г. Пермь Бадьина Лариса Ивановна
Создание многоуровневого списка Учитель информатики МАОУ "СОШ №55" г. Пермь Бадьина Лариса Ивановна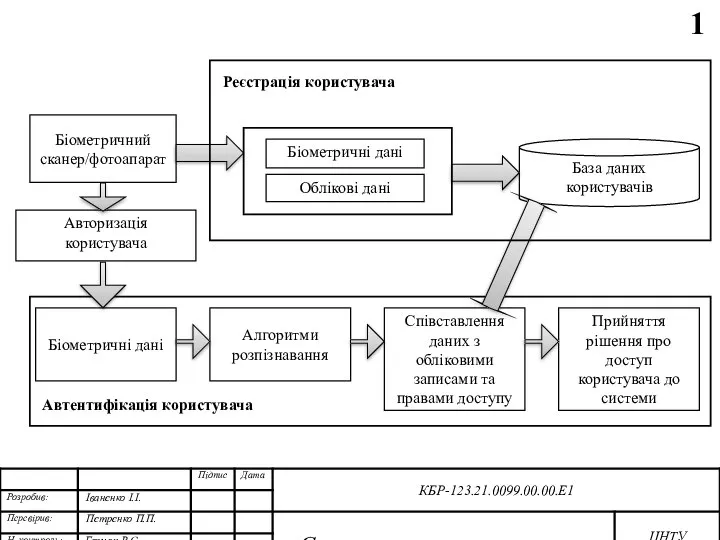 Приклад презентації. Реєстрація користувача
Приклад презентації. Реєстрація користувача Что такое журналистика?
Что такое журналистика? Управление исполнителями. Циклы с условием
Управление исполнителями. Циклы с условием Относительные и абсолютные ссылки
Относительные и абсолютные ссылки Компьютерное моделирование
Компьютерное моделирование Архитектура и применение системы энергоменеджмента EcoStruxure
Архитектура и применение системы энергоменеджмента EcoStruxure Алгоритмическая конструкция следование. Основные алгоритмические конструкции
Алгоритмическая конструкция следование. Основные алгоритмические конструкции Табличный процессор Excel. Практическая работа №2
Табличный процессор Excel. Практическая работа №2 Blu-ray. Преимущества Blu-ray
Blu-ray. Преимущества Blu-ray Жизненные ситуации и онлайн сервисы
Жизненные ситуации и онлайн сервисы Організаційно-правові засади захисту інформації
Організаційно-правові засади захисту інформації Звуки в презентации
Звуки в презентации О состоянии технического оснащения и персонала по поддержке системы
О состоянии технического оснащения и персонала по поддержке системы Что такое Google
Что такое Google Кодирование информации
Кодирование информации Презентация на тему Компьютерные очки и страшные сказки про мониторы
Презентация на тему Компьютерные очки и страшные сказки про мониторы  Машинный перевод
Машинный перевод Правовая информация. Информационные технологии
Правовая информация. Информационные технологии Восьмеричная и шестнадцатеричные системы счисления. Компьютерные системы счисления. Правило перевода целых десятичных чисел
Восьмеричная и шестнадцатеричные системы счисления. Компьютерные системы счисления. Правило перевода целых десятичных чисел Activation red RED BULL M.E.O. Communication with computer clubs
Activation red RED BULL M.E.O. Communication with computer clubs Знакомство с компьютером
Знакомство с компьютером Шаблон презентации
Шаблон презентации Задание 3. Снегопад
Задание 3. Снегопад