Матрицы. Действия над матрицами

Содержание:
Определение понятия матрица
Содержание матрицы
Свойства матриц
Сумма матриц
Произведение матриц
Вычитание матриц
Обратные матрицы

Матрица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов задаёт размер матрицы.
Иначе говоря, матрица — это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. Обозначают матрицы обычно простыми латинскими буквами: А, В,С...

Рассматриваемая матрица имеет 2 строки и 3 столбца.

Когда говорят о размерах матрицы, то сначала укызывают количество строк, а затем столбцов. Если количество строк и столбцов матрицы совпадает, то говорят о квадратной матрице.
Пример:
Матрица «три на три»

Элементы с одинаковыми индексами a11,a22, a33,...ann образуют главную диагональ квадратной матрицы, а элементы a1n, a2n-1, a3n-2....an1 ( т. е. Имеющие сумму индексов, равную n+1)-побочную диагональ. Единичной матрицей называется квадратная матрица, все элементы главной диагонали которой равны 1, а остальные элементы равны 0. Она обозначается буквой E. Нулевая матрица - это матрица, все элементы которой равны 0. Нулевая матрица может быть любого размера.

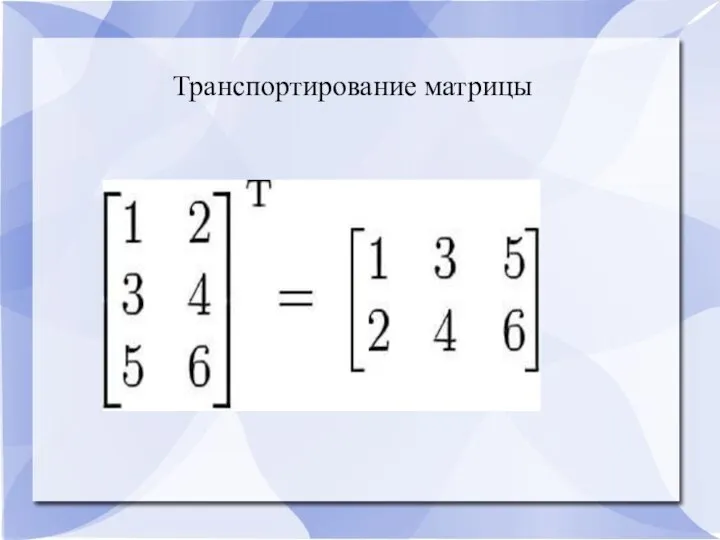
Транспортирование матрицы

Над матрицами можно выполнять определённые действия: сложение, вычитание и умножение. Также для матриц существуют особые действия — транспортирование матриц и нахождение обратной матрицы.

К числу линейных операций над матрицами относятся:
1)сложение матриц
2) умножение матриц на число

Суммой двух матриц А= (aij) и В= (bij) одинакового порядка называют матрицу С = (cij).

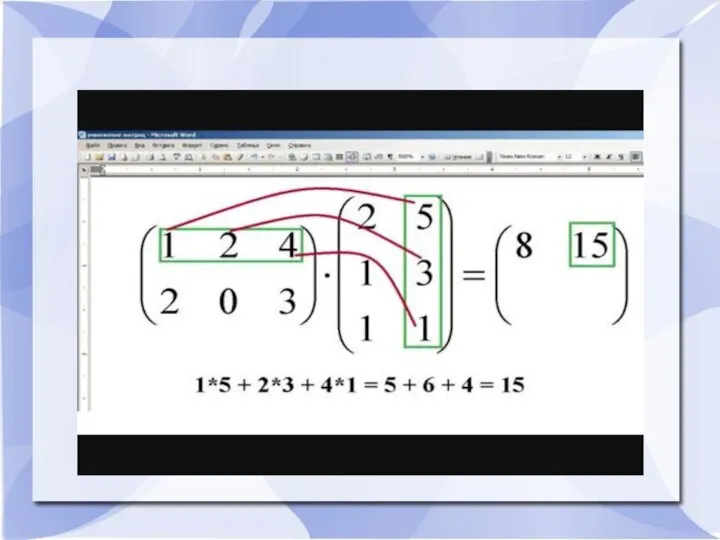
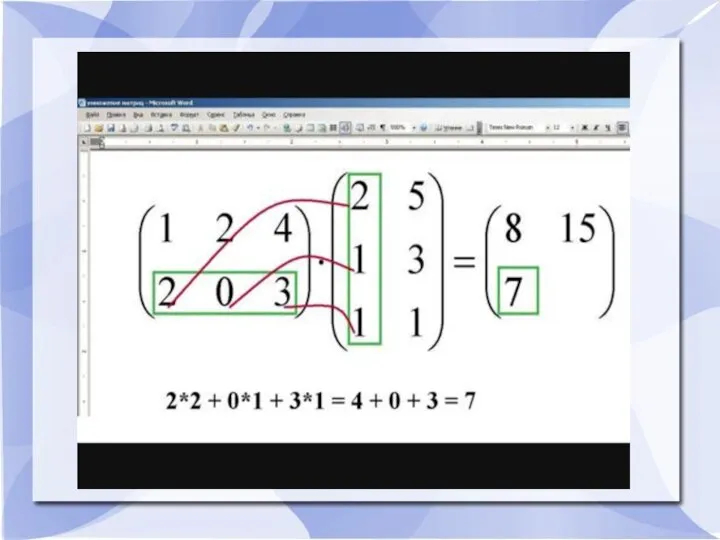
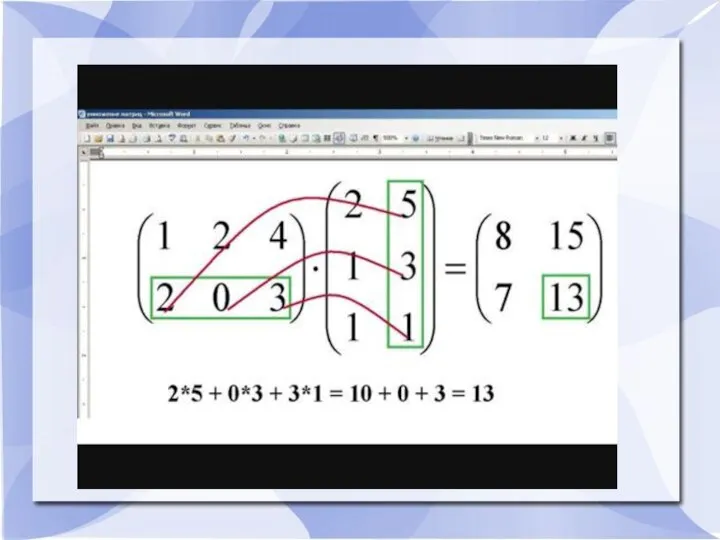
Умножение матрицы на матрицу

Разностью матриц A и B одного и того же размера называется матрица C=A-B такого же размера, которая получается из исходных матриц, путем вычитания из соответствующего элемента матрицы А соответствующего элемента матрицы B:

Обратной матрицей, к квадратной матрице A, называется такая матрица A в степени -1, для которой справедливо равенство A*A в степени -1= A в степени -1 *A=E

Определителем или детерминантом квадратной матрицы А = || aij || n*n называется число, которое ставится в соответствие этой матрицы.

Самостоятельная работа
Вариант 1 Вариант 2
1) А+В 1) А+В
А= 3 5 7 В= 1 2 4 А= 1 4 -2
2-1 0 2 3 2 10 2 -1
-5 -6 4
2) А-Н 2) А-В
Н= -4 3 -15 А= 4 2
-5 -7 0 9 0
А= 3 5 -17 В= 3 1
-1 0 10 -3 4

Самостоятельная работа
Вариант 1 Вариант 2
3) А*В 3) А*В
А= 0 2 3 А= 3 -1 2
4 5 6 4 2 0
-5 6 1
В= 7 10 13 В= 8 1
8 11 14 7 2
9 12 15
4) Транспортировать:
А= 5 7 9 В= 8 3 14
3 2 1 10 5 6