Содержание
- 2. Логические переменные и логические операции Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами: А, В,
- 3. Действия, совершаемые над логическими переменными для получения определенных логических функций, называются логическими операциями. 1. Логическая операция
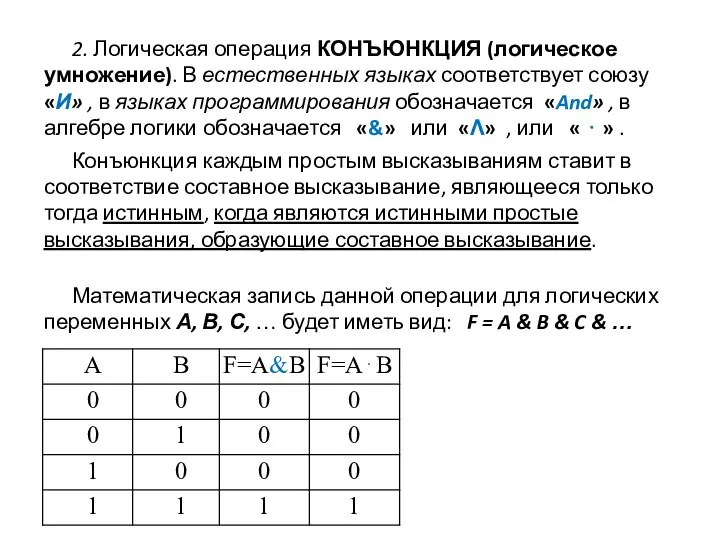
- 4. 2. Логическая операция КОНЪЮНКЦИЯ (логическое умножение). В естественных языках соответствует союзу «И» , в языках программирования
- 5. Пример: Дана функция F(A, B, C) = A Λ B Λ C. Определить значение логической функции
- 6. Пример: Дана функция F(A, B, C) = A Λ B Λ C. Определить значение логической функции
- 7. 3. Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение). В естественных языках соответствует союзу «ИЛИ», в языках программирования обозначается
- 8. Пример: Дана функция F(A, B, C) = A V B V C. Определить значение логической функции
- 9. Пример: Дана функция F(A, B, C) = A V B V C. Определить значение логической функции
- 10. 4. Логическая операция ИМПЛИКАЦИЯ (логическое следование). В естественных языках соответствует обороту речи, «если…, то …» ,
- 11. Пример: Дана функция F(A, B, C) = A V B → C. Определить значение логической функции
- 12. Пример: Дана функция F(A, B, C) = A V B → C. Определить значение логической функции
- 13. 5. Логическая операция ЭКВИВАЛЕНЦИЯ (логическая равнозначность). В естественных языках соответствует обороту речи «тогда и только тогда»,
- 14. Пример: Дана функция F(A, B, C) = A & ¬ B ↔ C. Определить значение логической
- 15. Пример: Дана функция F(A, B, C) = A & ¬ B ↔ C. Определить значение логической
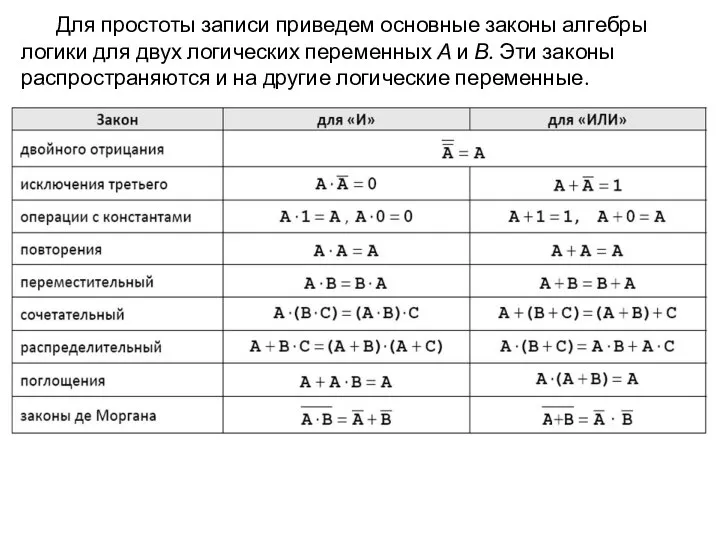
- 16. Для простоты записи приведем основные законы алгебры логики для двух логических переменных А и В. Эти
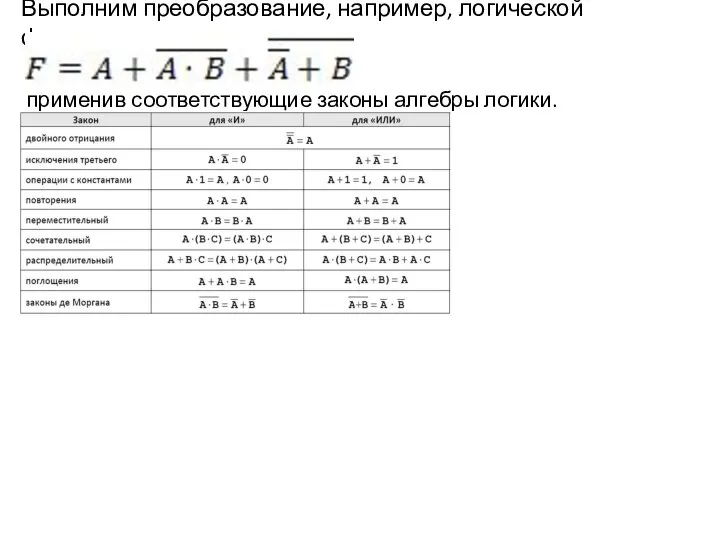
- 17. Выполним преобразование, например, логической функции применив соответствующие законы алгебры логики.
- 18. Выполним преобразование, например, логической функции применив соответствующие законы алгебры логики. C помощью законов алгебры логики можно
- 19. Выполним преобразование, например, логической функции применив соответствующие законы алгебры логики.
- 20. Выполним преобразование, например, логической функции применив соответствующие законы алгебры логики.
- 21. Выполним преобразование, например, логической функции применив соответствующие законы алгебры логики.
- 22. Выполним преобразование, например, логической функции применив соответствующие законы алгебры логики.
- 23. Выполним преобразование, например, логической функции применив соответствующие законы алгебры логики. 1
- 24. Выполним преобразование, например, логической функции применив соответствующие законы алгебры логики.
- 26. Логические функции и таблицы истинности Таблица истинности состоит из двух частей. Первая (левая) часть относится к
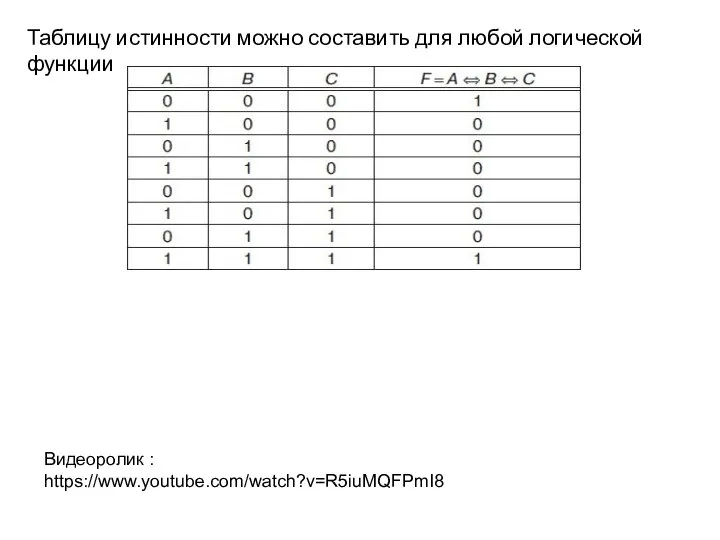
- 27. Таблицу истинности можно составить для любой логической функции Видеоролик : https://www.youtube.com/watch?v=R5iuMQFPmI8
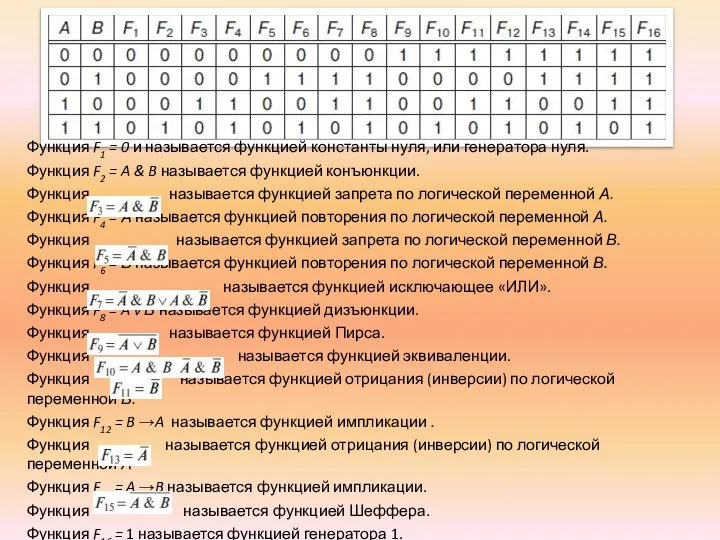
- 28. Функция F1 = 0 и называется функцией константы нуля, или генератора нуля. Функция F2 = A
- 29. Операцию замены одной логической функции другой в алгебре логики называют операцией суперпозиции или методом суперпозиции. Например,
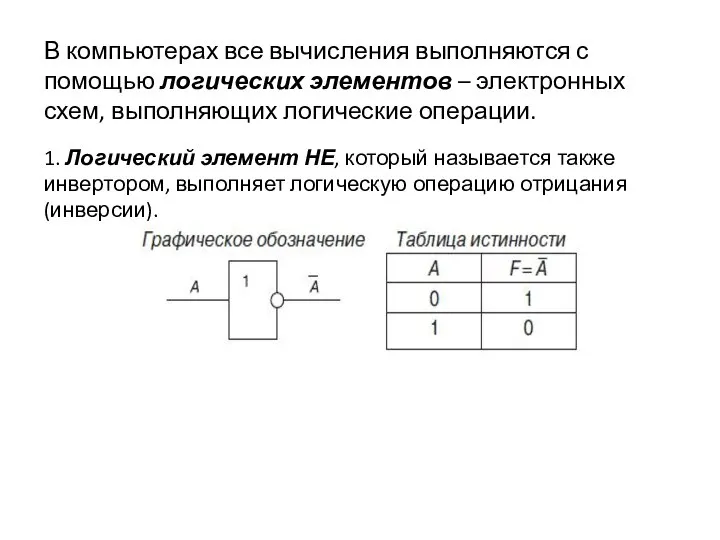
- 30. В компьютерах все вычисления выполняются с помощью логических элементов – электронных схем, выполняющих логические операции. 1.
- 31. 2. Логический элемент И, называемый также конъюнктором, выполняет операцию логического умножения (конъюнкции), теоретически может иметь бесконечное
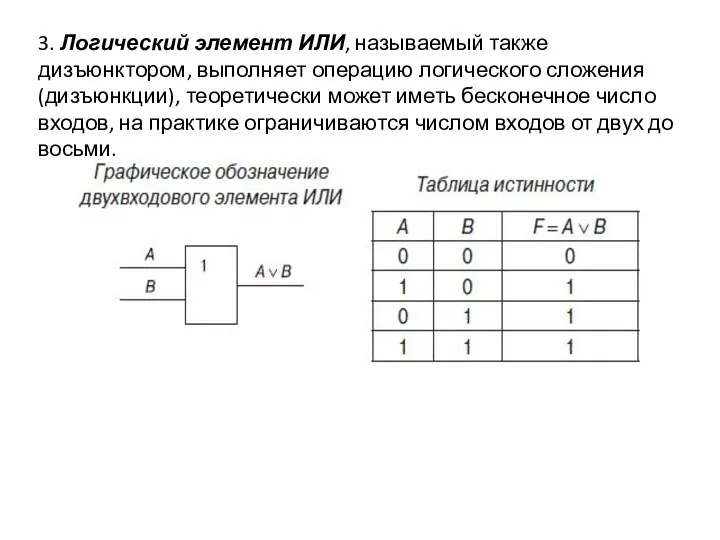
- 32. 3. Логический элемент ИЛИ, называемый также дизъюнктором, выполняет операцию логического сложения (дизъюнкции), теоретически может иметь бесконечное
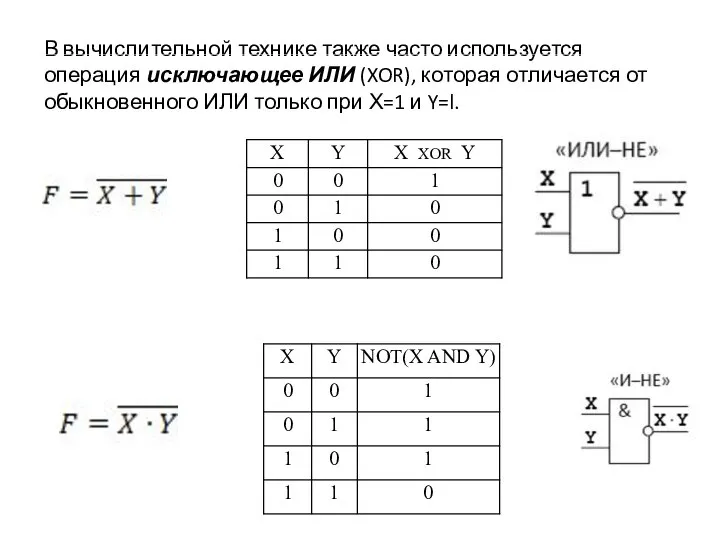
- 33. В вычислительной технике также часто используется операция исключающее ИЛИ (XOR), которая отличается от обыкновенного ИЛИ только
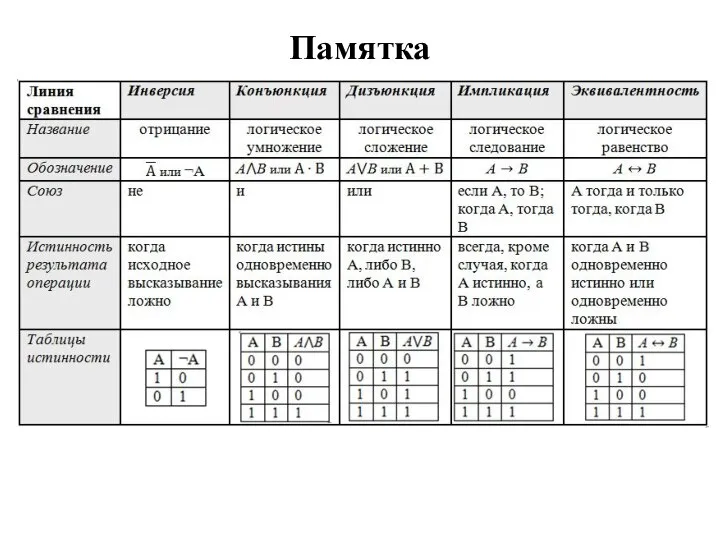
- 34. Памятка
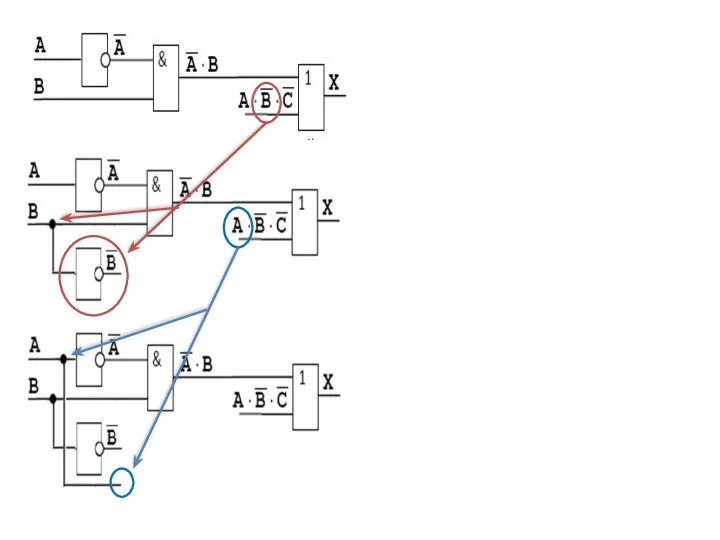
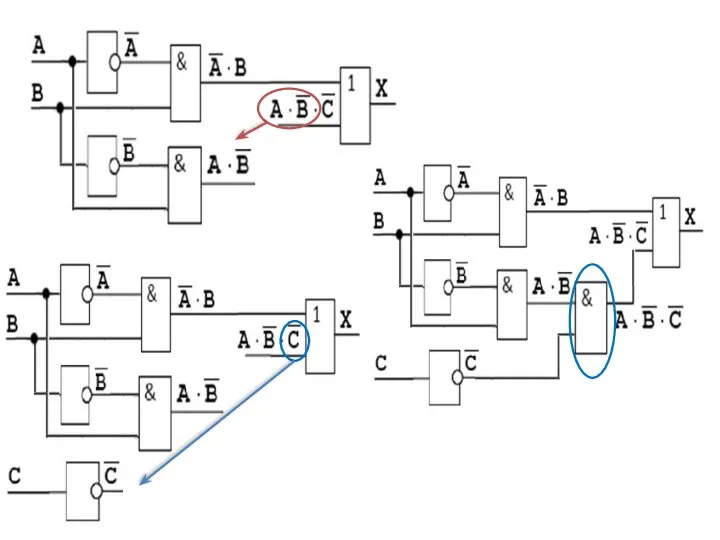
- 35. Составим схему, соответствующую выражению
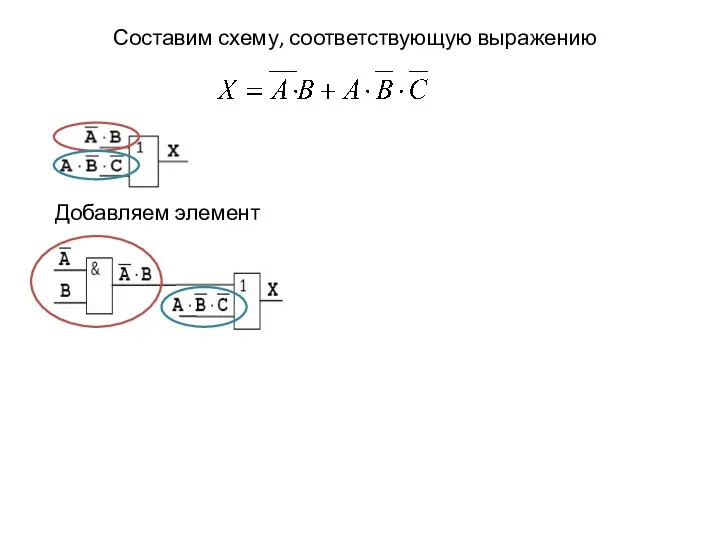
- 36. Составим схему, соответствующую выражению
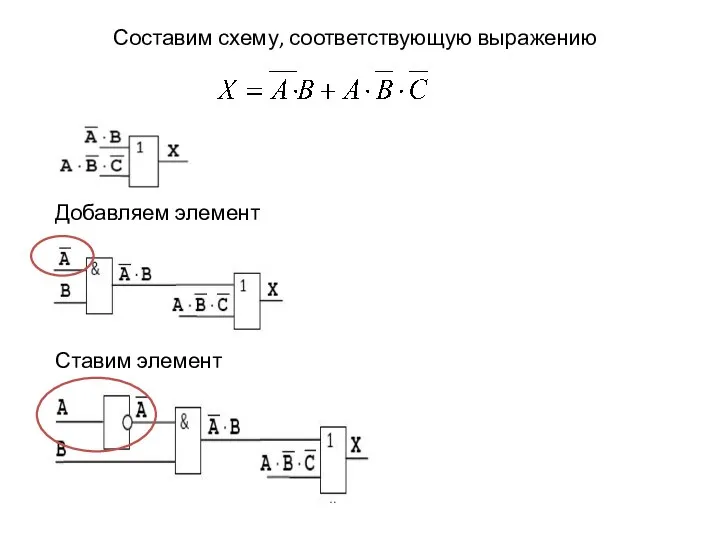
- 37. Составим схему, соответствующую выражению Добавляем элемент И:
- 38. Составим схему, соответствующую выражению Добавляем элемент И: Ставим элемент НЕ:
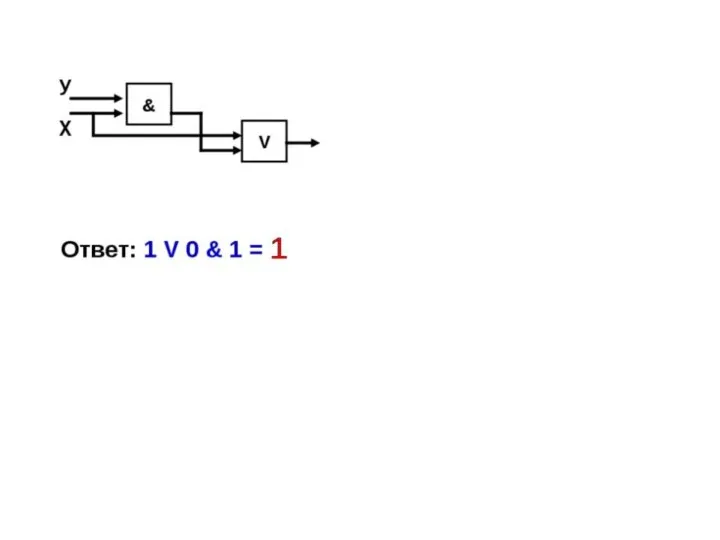
- 41. Составить логическую схему для следующего логического выражения: F= x V y & x (пусть x –
- 43. Домашнее задание. Используя законы алгебры логики упростить выражения:
- 45. Скачать презентацию




















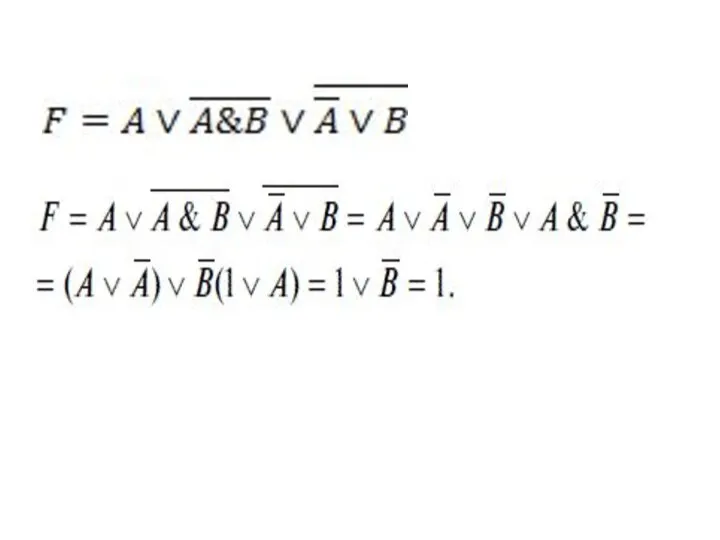







 Коммуникационная стратегия Новосибирской области. Разработка рекомендаций по упрощению работы Интернет-портала
Коммуникационная стратегия Новосибирской области. Разработка рекомендаций по упрощению работы Интернет-портала Поле Чудес
Поле Чудес Растровый графический редактор. CorelDraw: работа с каналами
Растровый графический редактор. CorelDraw: работа с каналами Изменение структуры таблицы. Удаление таблиц
Изменение структуры таблицы. Удаление таблиц Конфигурация CQM1H
Конфигурация CQM1H Понятие сетей и систем. Аппаратное обеспечение современных вычислительных машин
Понятие сетей и систем. Аппаратное обеспечение современных вычислительных машин Интересные факты из истории информатики
Интересные факты из истории информатики Дистанционные тренировки. Художественная гимнастика
Дистанционные тренировки. Художественная гимнастика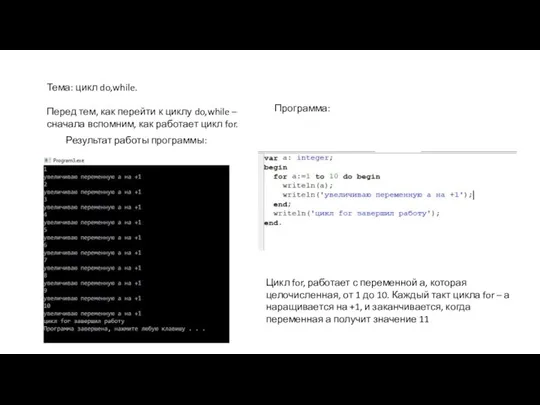 Цикл do, while
Цикл do, while Количество путей в графе
Количество путей в графе GPS система
GPS система Режимы передачи данных
Режимы передачи данных Sms-surprise.ru
Sms-surprise.ru Цифровая этнография и дьявольский значок уведомлений
Цифровая этнография и дьявольский значок уведомлений Систематизация и представление информации в виде сайта
Систематизация и представление информации в виде сайта Автоматизация схемы охраны и контроля образовательного учреждения
Автоматизация схемы охраны и контроля образовательного учреждения Урок информатики, 7 класс
Урок информатики, 7 класс Знаковые информационные модели
Знаковые информационные модели История развития вычислительной техники. 6 класс
История развития вычислительной техники. 6 класс 3D модели в программе SketchUp
3D модели в программе SketchUp Принципы построения телекоммуникационных вычислительных сетей (ТВС)
Принципы построения телекоммуникационных вычислительных сетей (ТВС) Дистанционное обучение
Дистанционное обучение MATLAB. C++ Builder
MATLAB. C++ Builder 129434
129434 Информационные технологии в юридической деятельности
Информационные технологии в юридической деятельности Внушительный дом
Внушительный дом Цифровому электромонтеру – цифровой медосмотр. Пилотный проект внедрения в ОАО МРСК Урала
Цифровому электромонтеру – цифровой медосмотр. Пилотный проект внедрения в ОАО МРСК Урала Віруси та антивіруси
Віруси та антивіруси