Методы и алгоритмы трехмерной графики

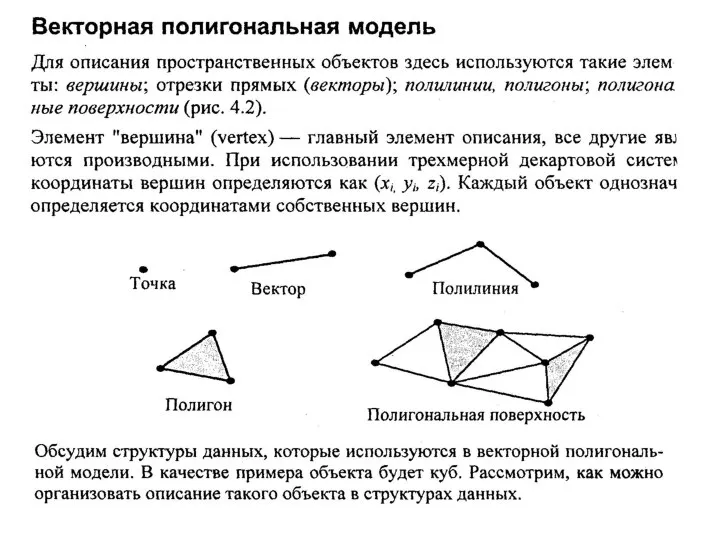
Содержание
Работа с 3D изображением
Аналитическая модель поверхности
Векторная полигональная модель
Задача удаления невидимых линий и поверхностей
Алгоритм Робертса
Алгоритм Варнока
Алгоритм Вейлера – Азертона
Метод Z- буфера
Алгоритм художника и плавающего горизонта

Для получения трёхмерного изображения на плоскости требуются следующие шаги:
моделирование — создание трёхмерной математической модели сцены и объектов в ней;
текстурирование — назначение поверхностям моделей растровых или процедурных текстур (подразумевает также настройку свойств материалов — прозрачность, отражения, шероховатость и пр.);
освещение — установка и настройка источников света;
анимация (в некоторых случаях) — придание движения объектам;
динамическая симуляция (в некоторых случаях) — автоматический расчёт взаимодействия частиц, твёрдых/мягких тел и пр. с моделируемыми силами гравитации, ветра, выталкивания и др., а также друг с другом;
рендеринг (визуализация) — построение проекции в соответствии с выбранной физической моделью;
композитинг (компоновка) — доработка изображения;
вывод полученного изображения на устройство вывода — дисплей или специальный принтер.

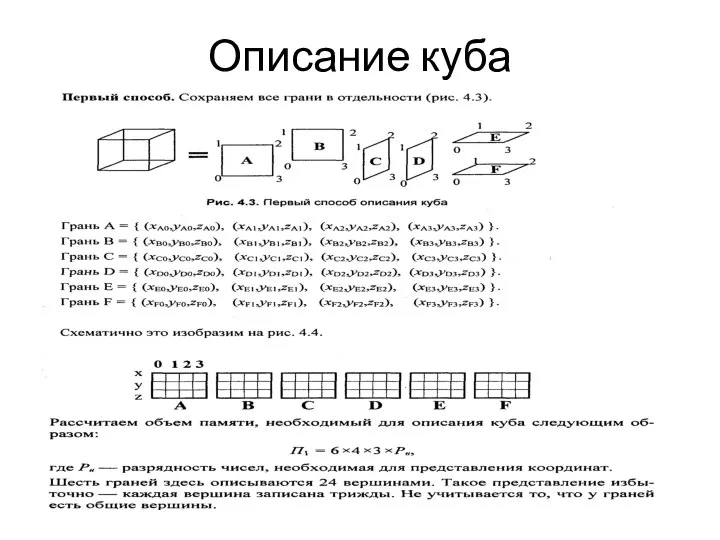
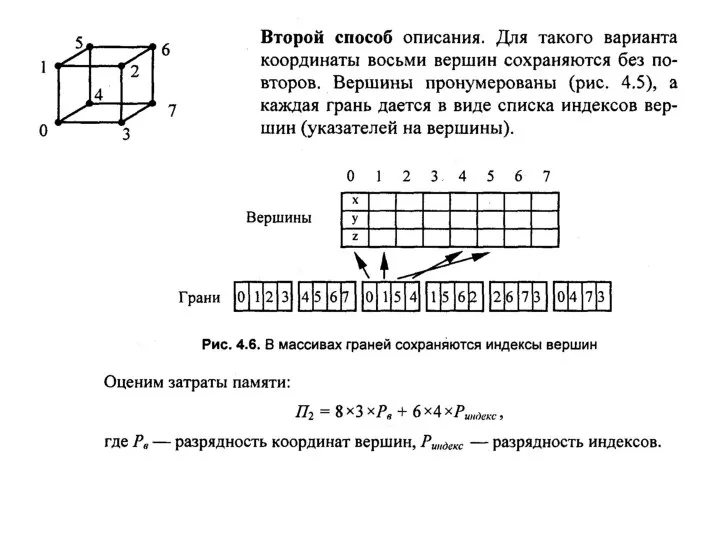
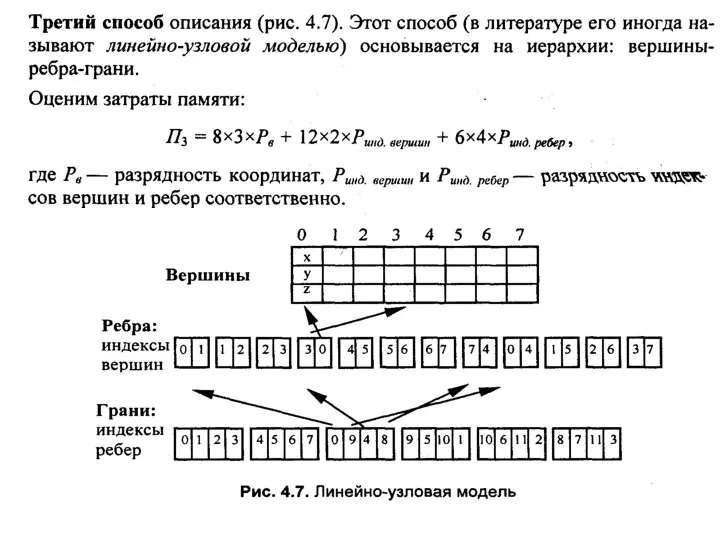
Описание куба

Оценка затрат ресурсов

Моделирование
Схема проецирования сцены на экран компьютера
Мо­де­ли­ро­ва­ние сцены (вир­ту­аль­но­го про­стран­ства мо­де­ли­ро­ва­ния) вклю­ча­ет в себя несколь­ко ка­те­го­рий объ­ек­тов:
Геометрия (построенная с помощью различных техник (напр., создание полигональной сетки) модель, например, здание);
Материалы (информация о визуальных свойствах модели, например, цвет стен и отражающая/преломляющая способность окон);
Источники света (настройки направления, мощности, спектра освещения);
Виртуальные камеры (выбор точки и угла построения проекции);
Силы и воздействия (настройки динамических искажений объектов, применяется в основном в анимации);
Дополнительные эффекты (объекты, имитирующие атмосферные явления: свет в тумане, облака, пламя и пр.)
За­да­ча трёх­мер­но­го мо­де­ли­ро­ва­ния — опи­сать эти объ­ек­ты и раз­ме­стить их в сцене с по­мо­щью гео­мет­ри­че­ских пре­об­ра­зо­ва­ний в со­от­вет­ствии с тре­бо­ва­ни­я­ми к бу­ду­ще­му изоб­ра­же­нию.

Задача удаления невидимых линий и поверхностей
Эта задача является одной из наиболее интересных и сложных в компьютерной графике.
Алгоритмы удаления заключаются в определении линий ребер, поверхностей или объемов, которые видимы или невидимы для наблюдателя, находящегося в заданной точке пространства.
Необходимость удаления невидимых линий, ребер, поверхностей или объемов проиллюстрирована на рис. 1. Рисунок наглядно демонстрирует, что изображение без удаления невидимых линий воспринимается неоднозначно.
Рис. 1. Неоднозначность восприятия изображения куба
Сложность задачи удаления невидимых линий и поверхностей привела к появлению большого числа различных способов ее решения.

Сортировка
Все алгоритмы такого рода так или иначе включают в себя сортировку, причем главная сортировка ведется по геометрическому расстоянию от тела, поверхности, ребра или точки до точки наблюдения или картинной плоскости.
Основная идея, положенная в основу сортировки по расстоянию, заключается в том, что чем дальше расположен объект от точки наблюдения, тем больше вероятность, что он будет полностью или частично заслонен одним из объектов, более близких к точке наблюдения.
После определения расстояний или приоритетов по глубине остается провести сортировку по горизонтали и по вертикали, чтобы выяснить, будет ли рассматриваемый объект действительно заслонен объектом, расположенным ближе к точке наблюдения.
Эффективность любого алгоритма удаления в значительной мере зависит от эффективности процесса сортировки.
Алгоритмы удаления невидимых линий или поверхностей можно классифицировать по способу выбора системы координат или пространства, в котором они работают.
Алгоритмы, работающие в объектном пространстве, имеют дело с мировой системой координат, в которой описаны эти объекты.
Алгоритмы же, работающие в пространстве изображения, имеют дело с системой координат того экрана, на котором объекты визуализируются.

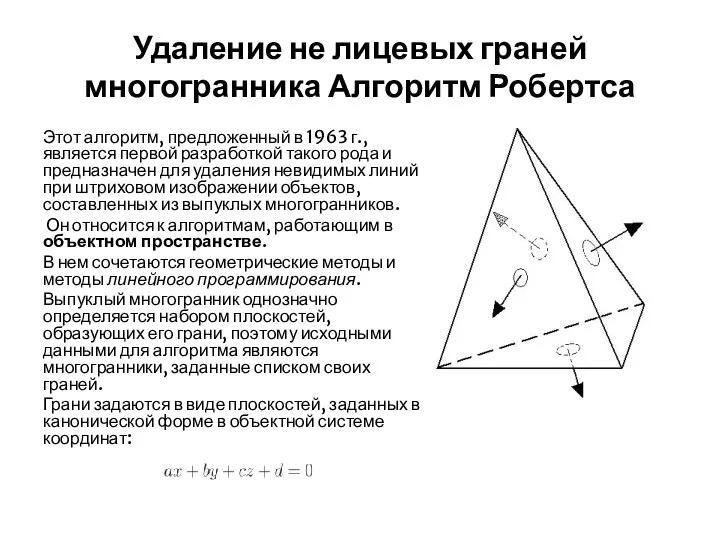
Удаление не лицевых граней многогранника Алгоритм Робертса
Этот алгоритм, предложенный в 1963 г., является первой разработкой такого рода и предназначен для удаления невидимых линий при штриховом изображении объектов, составленных из выпуклых многогранников.
Он относится к алгоритмам, работающим в объектном пространстве.
В нем сочетаются геометрические методы и методы линейного программирования.
Выпуклый многогранник однозначно определяется набором плоскостей, образующих его грани, поэтому исходными данными для алгоритма являются многогранники, заданные списком своих граней.
Грани задаются в виде плоскостей, заданных в канонической форме в объектной системе координат:

Векторное представление многогранника
Таким образом, каждая плоскость определяется четырехмерным вектором , а каждая точка , заданная в однородных координатах, также представляет собой четырехмерный вектор:
Принадлежность точки плоскости можно установить с помощью скалярного произведения, т.е. если , то точка принадлежит плоскости, если же нет, то знак произведения показывает, по какую сторону от плоскости эта точка находится.
В алгоритме Робертса плоскости строятся таким образом, что внутренние точки многогранника лежат в положительной полуплоскости.
Это означает, что вектор является внешней нормалью к многограннику
Из векторов плоскостей строится прямоугольная матрица порядка , которая называется обобщенной матрицей описания многогранника:

Алгоритм Робертса
Алгоритм прежде всего удаляет из каждого многогранника те ребра или грани, которые экранируются самим телом.
Робертс использовал для этого простой тест: если одна или обе смежные грани обращены своей внешней поверхностью к наблюдателю, то ребро является видимым.
Тест этот выполняется вычислением скалярного произведения координат наблюдателя на вектор внешней нормали грани: если результат отрицательный, то грань видима.
Затем каждое из видимых ребер каждого многогранника сравнивается с каждым из оставшихся многогранников для определения того, какая его часть или части, если таковые есть, экранируются этими телами.
Для этого в каждую точку ребра проводится отрезок луча, выходящего из точки расположения наблюдателя.
Если отрезок не пересекает ни одного из многогранников, то точка видима.
Для решения этой задачи используются параметрические уравнения прямой, содержащей ребро, и лучи.

Вычислительная часть алгоритма Робертса

Алгоритм Варнока
В отличие от алгоритма Робертса, Варнок в 1968 г. предложил алгоритм, работающий не в объектном пространстве, а в пространстве образа.
Он также нацелен на изображение многогранников, а главная идея его основана на гипотезе о способе обработки информации, содержащейся в сцене, глазом и мозгом человека.
Эта гипотеза заключается в том, что тратится очень мало времени и усилий на обработку тех областей, которые содержат мало информации.
Большая часть времени и труда затрачивается на области с высоким информационным содержимым.
В алгоритме Варнока и его вариантах делается попытка воспользоваться тем, что большие области изображения однородны.
Такое свойство называют когерентностью, имея в виду, что смежные области (пиксели) вдоль обеих осей х и у имеют тенденцию к однородности.

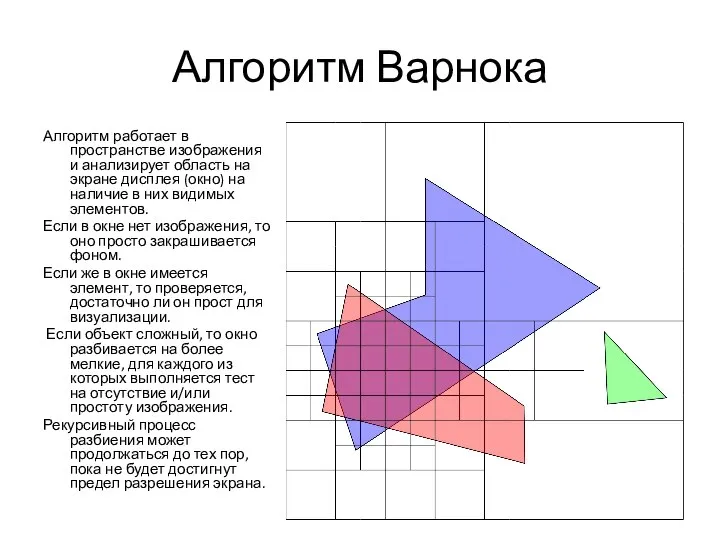
Алгоритм Варнока
Алгоритм работает в пространстве изображения и анализирует область на экране дисплея (окно) на наличие в них видимых элементов.
Если в окне нет изображения, то оно просто закрашивается фоном.
Если же в окне имеется элемент, то проверяется, достаточно ли он прост для визуализации.
Если объект сложный, то окно разбивается на более мелкие, для каждого из которых выполняется тест на отсутствие и/или простоту изображения.
Рекурсивный процесс разбиения может продолжаться до тех пор, пока не будет достигнут предел разрешения экрана.

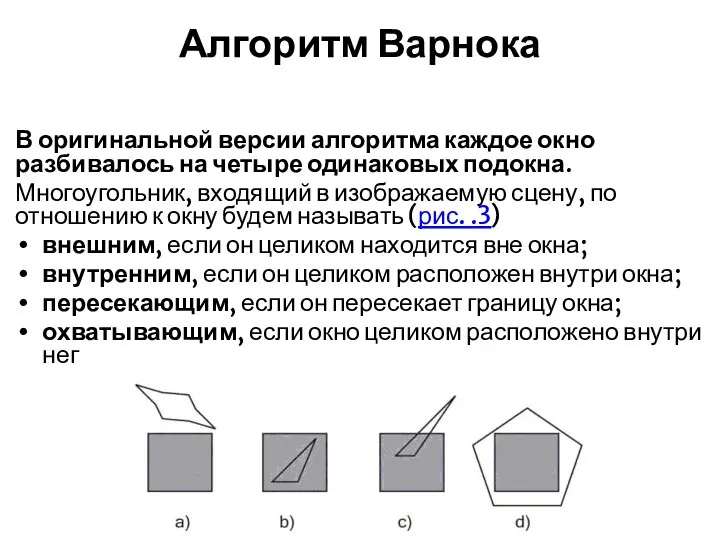
Алгоритм Варнока
В оригинальной версии алгоритма каждое окно разбивалось на четыре одинаковых подокна.
Многоугольник, входящий в изображаемую сцену, по отношению к окну будем называть (рис. .3)
внешним, если он целиком находится вне окна;
внутренним, если он целиком расположен внутри окна;
пересекающим, если он пересекает границу окна;
охватывающим, если окно целиком расположено внутри нег

Описание алгоритма Вернока
Для каждого окна:
Если все многоугольники сцены являются внешними по отношению к окну, то оно пусто; изображается фоновым цветом и дальнейшему разбиению не подлежит.
Если только один многоугольник сцены имеет общие точки с окном и является по отношению к нему внутренним, то окно заполняется фоновым цветом, а сам многоугольник заполняется своим цветом.
Если только один многоугольник сцены имеет общие точки с окном и является по отношению к нему пересекающим, то окно заполняется фоновым цветом, а часть многоугольника, принадлежащая окну, заполняется цветом многоугольника.
Если только один многоугольник охватывает окно и нет других многоугольников, имеющих общие точки с окном, то окно заполняется цветом этого многоугольника.
Если существует хотя бы один многоугольник, охватывающий окно, то среди всех таких многоугольников выбирается тот, который расположен ближе всех многоугольников к точке наблюдения, и окно заполняется цветом этого многоугольника.
В противном случае производится новое разбиение окна.

Комментарий к алгоритму Вернока
Шаги 1–4 рассматривают ситуацию пересечения окна только с одним многоугольником. Они используются для сокращения числа подразбиений.
Шаг 5 решает задачу удаления невидимых поверхностей. Многоугольник, находящийся ближе всех к точке наблюдения, экранирует все остальные.
Для реализации алгоритма необходимы функции, определяющие взаимное расположение окна и многоугольника, которые достаточно легко реализуются в случае прямоугольных окон и выпуклых многоугольников.
Для определения, является ли многоугольник охватывающим, внешним или внутренним, можно воспользоваться, например, погружением многоугольника в прямоугольную оболочку.

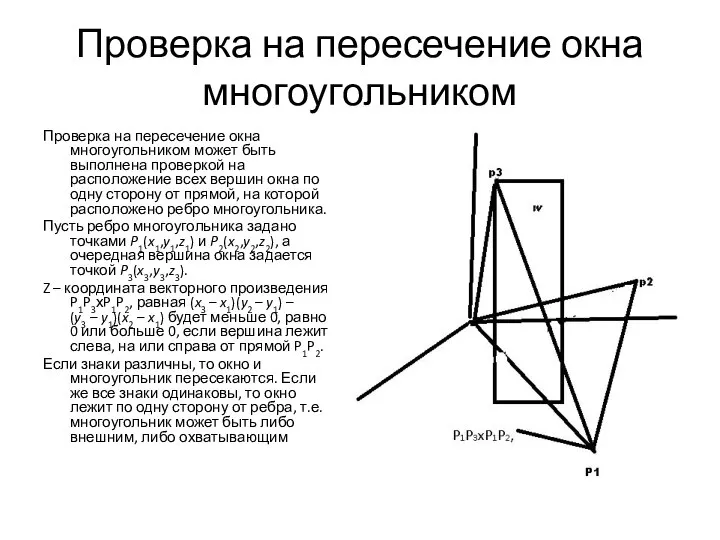
Проверка на пересечение окна многоугольником
Проверка на пересечение окна многоугольником может быть выполнена проверкой на расположение всех вершин окна по одну сторону от прямой, на которой расположено ребро многоугольника.
Пусть ребро многоугольника задано точками P1(x1,y1,z1) и P2(x2,y2,z2), а очередная вершина окна задается точкой P3(x3,y3,z3).
Z – координата векторного произведения P1P3хP1P2, равная (x3 – x1)(y2 – y1) – (y3 – y1)(x2 – x1) будет меньше 0, равно 0 или больше 0, если вершина лежит слева, на или справа от прямой P1P2.
Если знаки различны, то окно и многоугольник пересекаются. Если же все знаки одинаковы, то окно лежит по одну сторону от ребра, т.е. многоугольник может быть либо внешним, либо охватывающим

Сортировка многоугольников по глубине
Следует заметить, что существуют различные реализации алгоритма Варнока.
Были предложены варианты оптимизации, использующие предварительную сортировку многоугольников по глубине, т. е. по расстоянию от точки наблюдения, и другие.
Этот случай фактически сводится к поиску охватывающего многоугольника, перекрывающего все остальные многоугольники, связанные с окном. Проверка на такой многоугольник может быть выполнена следующим образом: в угловых точках окна вычисляются Z-координаты для всех многоугольников, связанных с окном.
Если все четыре такие Z-координаты охватывающего многоугольника ближе к наблюдателю, чем все остальные, то окно закрашивается цветом соответствующего охватывающего многоугольника.
Если же нет, то мы имеем сложный случай и разбиение следует продолжить.

Алгоритм Вейлера-Азертона
Вейлер и Азертон попытались оптимизировать алгоритм Варнока в отношении числа выполняемых разбиений, перейдя от прямоугольных разбиений к разбиениям вдоль границ многоугольников (1977).
Для этого они использовали ими же разработанный алгоритм отсечения многоугольников. Алгоритм работает в объектном пространстве, и результатом его работы являются многоугольники.
В самом общем виде он состоит из четырех шагов.
Предварительная сортировка по глубине.
Отсечение по границе ближайшего к точке наблюдения многоугольника, называемое сортировкой многоугольников на плоскости.
Удаление многоугольников, экранируемых более близкими к точке наблюдения многоугольниками.
Если требуется, то рекурсивное разбиение и новая сортировка.

Алгоритм Вейлера-Азертона
В самом общем виде он состоит из четырех шагов.
Предварительная сортировка по глубине.
Отсечение по границе ближайшего к точке наблюдения многоугольника, называемое сортировкой многоугольников на плоскости.
Удаление многоугольников, экранируемых более близкими к точке наблюдения многоугольниками.
Если требуется, то рекурсивное разбиение и новая сортировка

Алгоритм Вейлера-Азертона
В процессе предварительной сортировки создается список приблизительных приоритетов, причем близость многоугольника к точке наблюдения определяется расстоянием до ближайшей к ней вершины.
Затем выполняется отсечение по самому первому из многоугольников.
Отсечению подвергаются все многоугольники из списка, причем эта операция выполняется над проекциями многоугольников на картинную плоскость.
При этом создаются списки внешних и внутренних фигур.
Все попавшие в список внешних не экранируются отсекающим многоугольником.
Затем рассматривается список внутренних многоугольников и выполняется сортировка по расстоянию до отсекающего многоугольника.
Если все вершины некоторого многоугольника оказываются дальше от наблюдателя, чем самая удаленная из вершин экранирующего, то они невидимы, и тогда они удаляются.
После этого работа алгоритма продолжается с внешним списком.
Если какая-то из вершин внутреннего многоугольника оказывается ближе к наблюдателю, чем ближайшая из вершин экранирующего многоугольника, то такой многоугольник является частично видимым.
В этом случае предварительный список приоритетов некорректен, и тогда в качестве нового отсекающего многоугольника выбирается именно этот "нарушитель порядка".
При этом используется именно исходный многоугольник, а не тот, что получился в результате первого отсечения.

Алгоритм был обобщен Кэтмулом
Этот алгоритм в дальнейшем был обобщен Кэтмулом (1974) для изображения гладких бикубических поверхностей.
Его подход заключался в том, что разбиению подвергалась поверхность.
Алгоритм Кэтмула можно описать так:
Рекурсивно разбивается поверхность до тех пор, пока проекция элемента на плоскость изображения не будет покрывать не больше одного пикселя.
Определить атрибуты поверхности в этом пикселе и изобразить его.
Эффективность такого метода, как и алгоритм Варнока, зависит от эффективности разбиений.
В дальнейшем этот алгоритм был распространен на сплайновые поверхности.

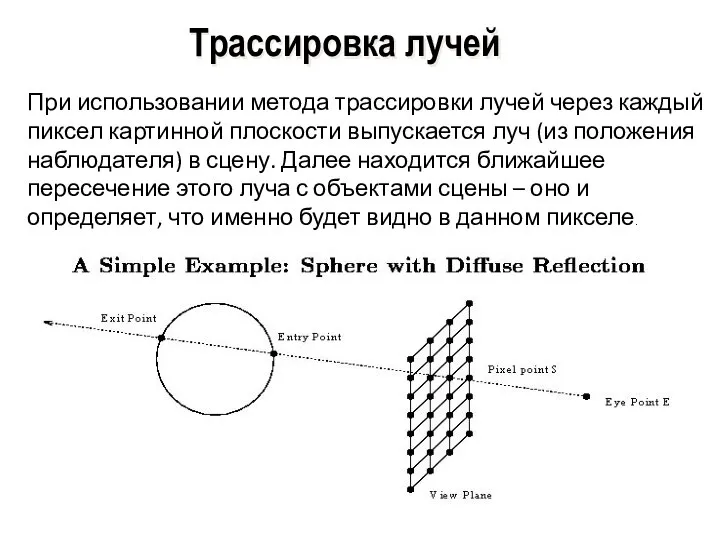
Трассировка лучей
При использовании метода трассировки лучей через каждый пиксел картинной плоскости выпускается луч (из положения наблюдателя) в сцену. Далее находится ближайшее пересечение этого луча с объектами сцены – оно и определяет, что именно будет видно в данном пикселе.

Метод буфера глубины
Каждому пикселу картинной плоскости, кроме значения цвета, хранящемуся в буфере кадра, сопоставляется еще значение глубины (расстояние вдоль направления проектирования от картинной плоскости до соответствующей точки пространства).
foreach(p in pixels)
if(p.z < zBuffer[p.x, p.y])
draw( p );
zBuffer[p.x, p.y] = p.z;
}

Метод Z-буфера
Это один из простейших алгоритмов удаления невидимых поверхностей.
Впервые он был предложен Кэтмулом в 1975 г.
Работает этот алгоритм в пространстве изображения.
Идея Z-буфера является простым обобщением идеи о буфере кадра.
Буфер кадра используется для запоминания атрибутов каждого пикселя в пространстве изображения, а Z-буфер предназначен для запоминания глубины (расстояния от картинной плоскости) каждого видимого пикселя в пространстве изображения.
Поскольку достаточно распространенным является использование координатной плоскости в качестве картинной плоскости, то глубина равна координате точки, отсюда и название буфера.
В процессе работы значение глубины каждого нового пикселя, который нужно занести в буфер кадра, сравнивается с глубиной того пикселя, который уже занесен в Z-буфер.
Если это сравнение показывает, что новый пиксель расположен впереди пикселя, находящегося в буфере кадра, то новый пиксель заносится в этот буфер и, кроме того, производится корректировка Z-буфера новым значением глубины.
Если же сравнение дает противоположный результат, то никаких действий не производится.
По сути, алгоритм является поиском по x и y наибольшего значения функции .

Достоинства и недостатки алгоритма z - буфера
Главное преимущество алгоритма - его простота.
Кроме того, этот алгоритм решает задачу об удалении невидимых поверхностей и делает тривиальной визуализацию пересечений сложных поверхностей.
Сцены могут быть любой сложности. Поскольку габариты пространства изображения фиксированы, оценка вычислительной трудоемкости алгоритма не более чем линейна.
Поскольку элементы сцены или картинки можно заносить в буфер кадра или в Z-буфер в произвольном порядке, их не нужно предварительно сортировать по приоритету глубины.
Поэтому экономится вычислительное время, затрачиваемое на сортировку по глубине.
Основной недостаток алгоритма - большой объем требуемой памяти.
В последнее время в связи с быстрым ростом возможностей вычислительной техники этот недостаток становится менее лимитирующим
В предельном варианте можно использовать буфер размером в одну строку развертки.
Для последнего случая был разработан алгоритм построчного сканирования.
Поскольку каждый элемент сцены обрабатывается много раз, то сегментирование Z-буфера, вообще говоря, приводит к увеличению времени, необходимого для обработки сцены.
Другой недостаток алгоритма состоит в трудоемкости реализации эффектов, связанных с полупрозрачностью, и ряда других специальных задач, повышающих реалистичность изображения.
Поскольку алгоритм заносит пиксели в буфер кадра в произвольном порядке, то довольно сложно получить информацию, которая необходима для методов, основывающихся на предварительном анализе сцены.

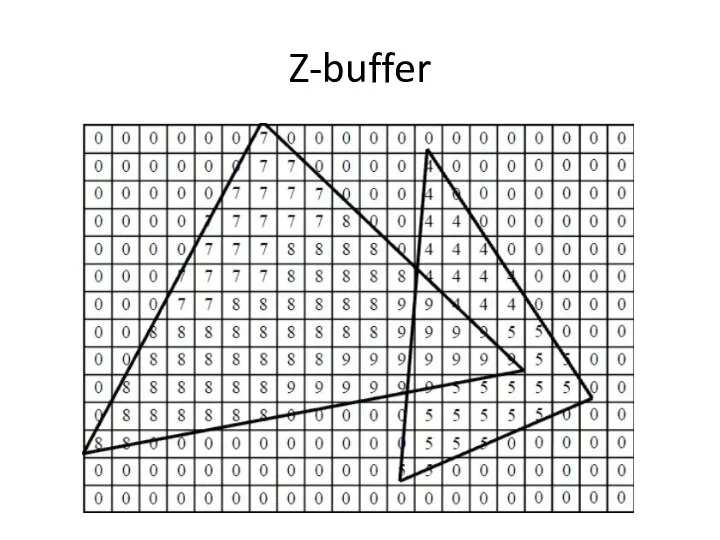
Заполнение Z-buffer
Буфер глубины (Z-buffer, depth buffer) — дополнительный объем памяти, где хранится значение глубины примитивов передней поверхности (расстояние от наблюдателя до поверхности изображаемого объекта) для каждого пикселя
Размеры Z-буфера равны размерам окна, таким образом, каждому пикселю окна соответствует ячейка Z-буфера. В этой ячейке хранится значение глубины пикселя (рис.). Перед растеризацией сцены Z-буфер заполняется значением, соответствующим максимальной глубине. В случае, когда глубина характеризуется значением w, максимальной глубине соответствует нулевое значение.
Анализ видимости происходит при растеризации граней, для каждого пикселя рассчитывается глубина и сравнивается со значением в Z-буфере, если рисуемый пиксель ближе (его w больше значения в Z-буфере), то пиксель рисуется, а значение в Z-буфере заменяется его глубиной.
Если пиксель дальше, то пиксель не рисуется и Z-буфер не изменяется, текущий пиксель дальше того, что нарисован ранее, а значит, невидим.

Z-buffer

Метод Z-буфера
Алгоритм довольно просто реализуется как программно, так и аппаратно, прекрасно сочетается с конвейерной архитектурой графической системы и может выполняться со скоростью, соответствующей скорости обработки вершин остальными модулями конвейера.
Хотя алгоритм отталкивается от пространства изображения, он включает цикл просмотра многоугольников, а не пикселей и может быть реализован в процессе растрового преобразования.
Предположим, что выполняется растровое преобразование одного из двух многоугольников, показанных на рис.
Используя принятую в графической системе модель закрашивания, можно вычислить цвет точек пересечения с каждым из многоугольников луча, исходящего из центра проецирования и проходящего через заданный пиксель картинной плоскости.
Кроме того, одновременно нужно определить, является ли данная точка пересечения видимой наблюдателю, из двух анализируемых видимой будет только точка, ближайшая к наблюдателю.

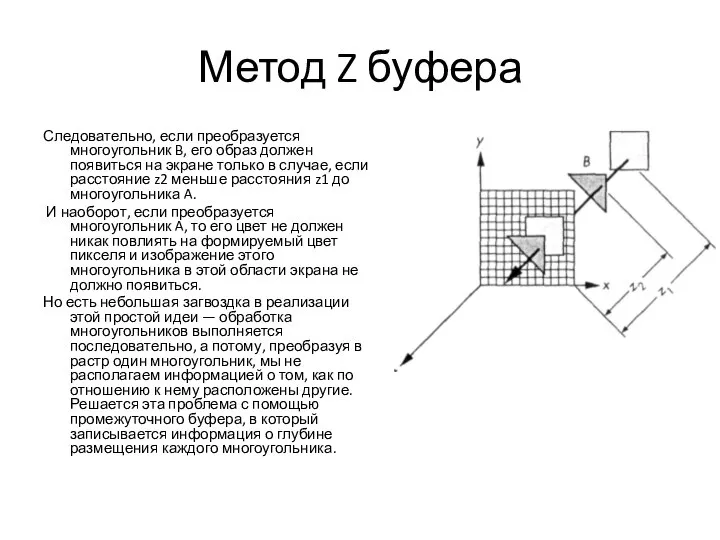
Метод Z буфера
Следовательно, если преобразуется многоугольник B, его образ должен появиться на экране только в случае, если расстояние z2 меньше расстояния z1 до многоугольника A.
И наоборот, если преобразуется многоугольник A, то его цвет не должен никак повлиять на формируемый цвет пикселя и изображение этого многоугольника в этой области экрана не должно появиться.
Но есть небольшая загвоздка в реализации этой простой идеи — обработка многоугольников выполняется последовательно, а потому, преобразуя в растр один многоугольник, мы не располагаем информацией о том, как по отношению к нему расположены другие. Решается эта проблема с помощью промежуточного буфера, в который записывается информация о глубине размещения каждого многоугольника.

Метод Z-буфера
Предположим, что в нашем распоряжении имеется буфер — назовем его Zбуфером, который имеет такую же организацию, как и буфер кадра, а разрядность каждой ячейки достаточна для хранения информации о глубине с приемлемой для качества изображения точностью.
Например, если формат изображения 1024×1280 пикселей и расстояние в графической системе представляется действительным числом с однократной точностью, то в Z-буфере должно быть 1024×1280 32-разрядных ячеек.
Перед началом растрового преобразования объектов сцены в каждую ячейку заносится код, соответствующий максимальному расстоянию от центра проецирования.
Буфер кадра в исходном состоянии заполняется кодами цвета фона. В процессе растрового преобразования объектов каждая ячейка Z-буфера содержит значение расстояния до ближайшего из обработанных ранее многоугольников вдоль проецирующего луча, проходящего через соответствующий пиксель пространства изображения.

Метод Z-буфера
Процесс заполнения Z-буфера выглядит в первом приближении следующим образом. Все многоугольники в описании сцены последовательно, один за другим, подвергаются растровому преобразованию.
Для каждой точки на многоугольнике, которая проецируется на определенный пиксель, вычисляется расстояние до центра проецирования.
Это расстояние сравнивается с уже хранящимся в той ячейке Z-буфера, которая соответствует формируемому пикселю.
Если расстояние до текущего многоугольника больше хранящегося в Z-буфере, значит, ранее был обработан многоугольник, расположенный ближе к наблюдателю, который, таким образом, загораживает текущий.
Следовательно, данная точка текущего многоугольника не будет видима и информацию о ее цвете не нужно заносить в буфер кадра.
Если же вычисленное расстояние меньше того, что хранится в Z-буфере, значит, текущий многоугольник сам загораживает те, что были обработаны ранее, и его код цвета должен заменить в буфере кадра код цвета, сформированный ранее.
Одновременно вычисленное только что расстояние заносится в соответствующую ячейку Z-буфера.

Методы приоритетов (художника, плавающего горизонта)
Рассмотрим группу методов, учитывающих специфику изображаемой сцены для удаления невидимых линий и поверхностей.
При изображении сцен со сплошным закрашиванием поверхностей можно воспользоваться методом художника:
элементы сцены изображаются в последовательности от наиболее удаленных от наблюдателя к более близким.
При экранировании одних участков сцены другими невидимые участки просто закрашиваются.
Если вычислительная трудоемкость получения изображения для отдельных элементов достаточно высока, то такой алгоритм будет не самым лучшим по эффективности, но зато мы избежим анализа (и вполне возможно, тоже дорогостоящего), позволяющего установить, какие же из элементов изображать не надо в силу их невидимости.
Например, при изображении правильного многогранника мы довольно легко можем упорядочить его грани по глубине, но такая сортировка для произвольного многогранника возможна далеко не всегда.

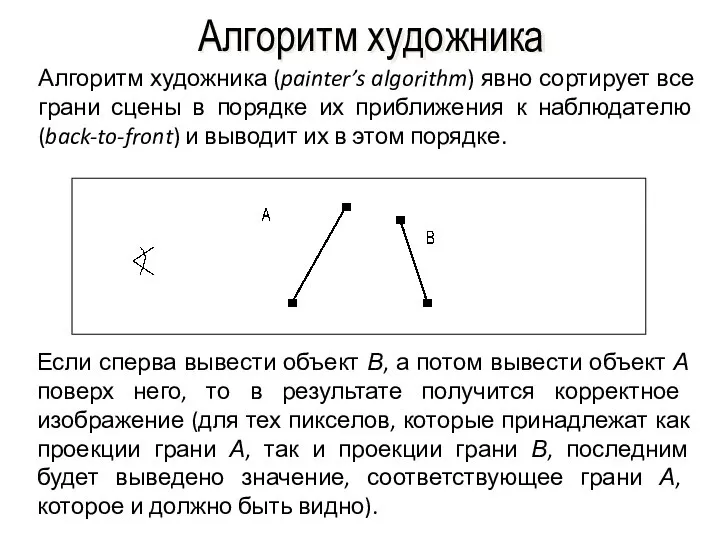
Алгоритм художника
Алгоритм художника (painter’s algorithm) явно сортирует все грани сцены в порядке их приближения к наблюдателю (back-to-front) и выводит их в этом порядке.
Если сперва вывести объект В, а потом вывести объект А поверх него, то в результате получится корректное изображение (для тех пикселов, которые принадлежат как проекции грани А, так и проекции грани В, последним будет выведено значение, соответствующее грани А, которое и должно быть видно).

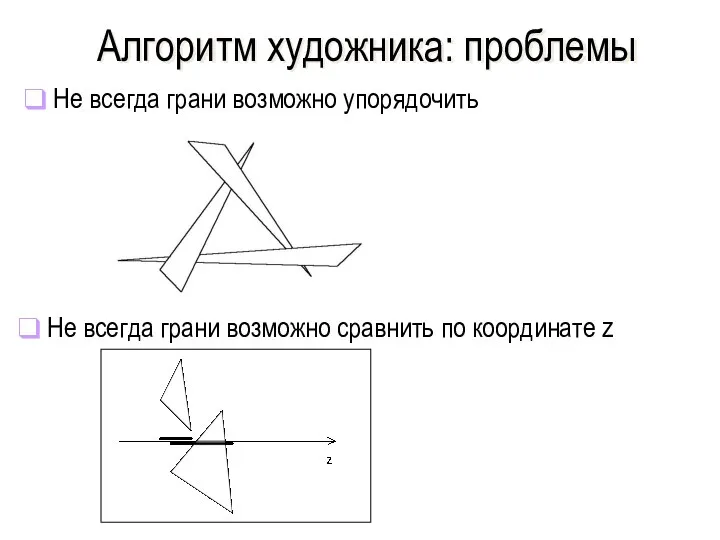
Алгоритм художника: проблемы
Не всегда грани возможно упорядочить
Не всегда грани возможно сравнить по координате z

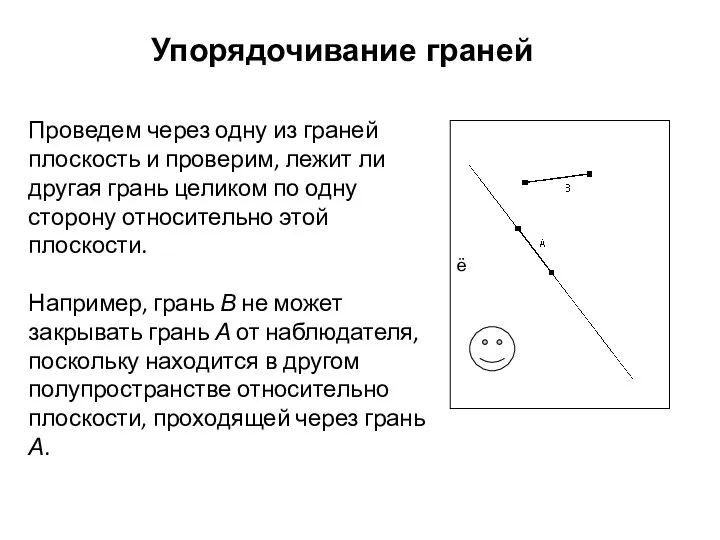
ё
Упорядочивание граней
Проведем через одну из граней плоскость и проверим, лежит ли другая грань целиком по одну сторону относительно этой плоскости.
Например, грань В не может закрывать грань А от наблюдателя, поскольку находится в другом полупространстве относительно плоскости, проходящей через грань А.

Пять проверок в алгоритме художника
1. Накладываются ли x-габариты мн-ков?
2. Накладываются ли y-габариты мн-ков?
3. P полностью за плоскостью Q по отношению к наблюдателю?
4. Q полностью перед плоскостью P по отношению к наблюдателю?
5. Пересекаются ли проекции многоугольников на плоскость (x, y)?

Метод двоичного разбиения пространства (1/3)
Пусть известно, что плоскость π разбивает все грани (объекты) сцены на два непересекающихся множества в зависимости от того, в каком полупространстве по отношению к данной плоскости они лежат
Тогда ни одна из граней, лежащих в том же полупространстве, что и наблюдатель, не может быть закрыта ни одной из граней из другого полупространства. Таким образом, удалось осуществить частичное упорядочение граней исходя из возможности загораживания друг друга.

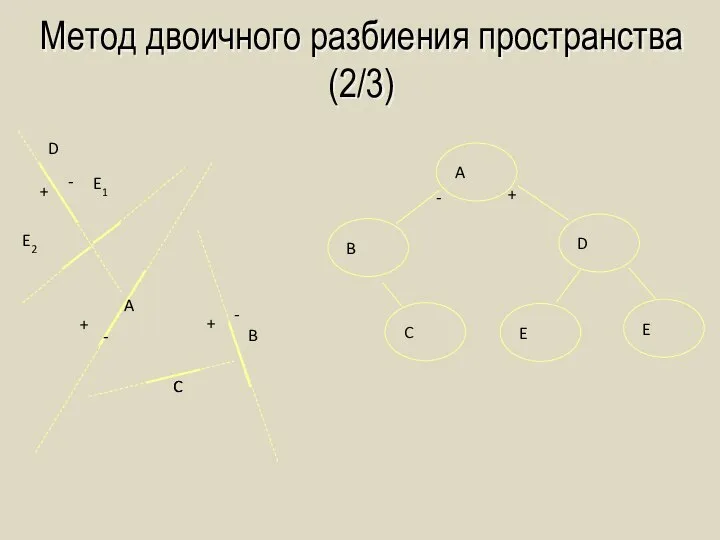
Метод двоичного разбиения пространства (2/3)
A
B
C
D
C
E1
E2
+
-
+
-
+
-
A
B
C
D
E
E
+
-

Метод двоичного разбиения пространства (3/3)
class BSPNode {
Face *face; // Грань объекта BSPNode *positive;
BSPNode *negative;
…
}
void BSPNode::Draw() {
if(face->Sign(viewer) == 1) {
if(negative) negative->Draw();
face->Draw();
if(positive) positive->Draw();
} else {
if(positive) positive->Draw();
face->Draw();
if(negative) negative->Draw();
}
}

Изображение поверхности, заданной в виде однозначной функции двух переменных

Метод плавающего горизонта
Алгоритм художника можно применять для полностью закрашенной сцены, а для каркасного изображения, когда объект представляется в виде набора кривых или ломаных линий, он непригоден.
Для этого случая предложен еще один метод, весьма эффективный - метод плавающего горизонта.
Вернемся к предыдущему примеру изображения поверхности. Каркасное изображение получается путем изображения кривых, получаемых при пересечении этой поверхности плоскостями x=xi и y=yi (рис. ).
На самом деле мы будем рисовать четырехугольник и одну диагональ.
В процессе рисования нам понадобятся два целочисленных массива: (нижний горизонт) и (верхний горизонт) размерностью, соответствующей горизонтальному размеру экрана в пикселях.
Они нужны для анализа видимости участков изображаемых отрезков.
Сначала мы инициализируем верхний горизонт нулем, а нижний - максимальным значением вертикальной координаты на экране.
Каждая выводимая на экран точка может закрывать другие точки, которые "скрываются за горизонтом".
По мере рисования нижний горизонт "опускается", а верхний "поднимается", постепенно оставляя все меньше незакрытого пространства.
В отличие от метода художника, здесь мы продвигаемся от ближнего угла к дальнему.

Алгоритм плавающего горизонта
Алгоритм плавающего горизонта можно отнести к классу алгоритмов, работающих в пространстве изображения. Алгоритм плавающего горизонта чаше всего используется для удаления невидимых линий трехмерного представления функций, описывающих поверхность в виде
F(x, у, z) = 0.
Подобные функции возникают во многих приложениях в математике, технике, естественных науках и других дисциплинах.
Главная идея данного метода заключается в сведении трехмерной задачи к двумерной путем пересечения исходной поверхности последовательностью параллельных секущих плоскостей, имеющих постоянные значения координат х, у или z.
На рис. приведен пример, где указанные параллельные плоскости определяются постоянными значениями z.
Функция F(x,у,z) = 0 сводится к последовательности кривых, лежащих в каждой из этих параллельных плоскостей, например к последовательности у=f(x,z) или х=g(у,z), где z постоянно на каждой из заданных параллельных плоскостей.

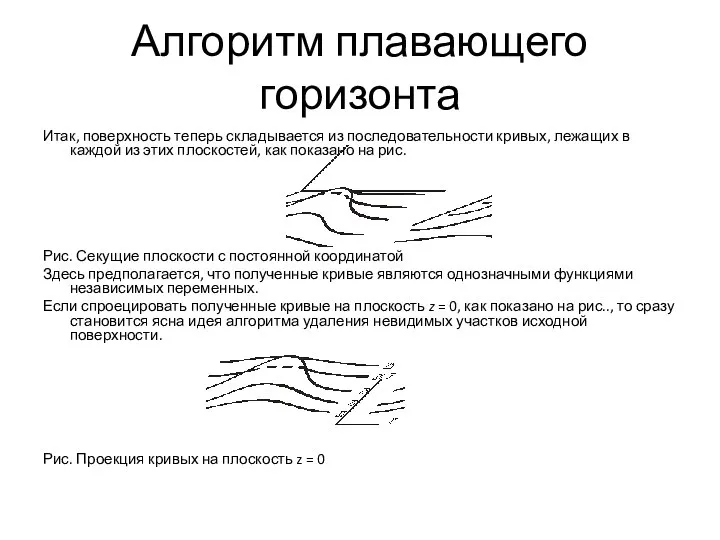
Алгоритм плавающего горизонта
Итак, поверхность теперь складывается из последовательности кривых, лежащих в каждой из этих плоскостей, как показано на рис.
Рис. Секущие плоскости с постоянной координатой
Здесь предполагается, что полученные кривые являются однозначными функциями независимых переменных.
Если спроецировать полученные кривые на плоскость z = 0, как показано на рис.., то сразу становится ясна идея алгоритма удаления невидимых участков исходной поверхности.
Рис. Проекция кривых на плоскость z = 0

Алгоритм плавающего горизонта
Алгоритм сначала упорядочивает плоскости z = const по возрастанию расстояния до них от точки наблюдения. Затем для каждой плоскости, начиная с ближайшей к точке наблюдения, строится кривая, лежащая на ней, т. е. для каждого значения координаты х в пространстве изображения определяется соответствующее значение y. Алгоритм удаления невидимой линии заключается в следующем.
Если на текущей плоскости при некотором заданном значении x соответствующее значение у на кривой больше значения y для всех предыдущих кривых при этом значении x, то текущая кривая видима в этой точке; в противном случае она невидима.
Невидимые участки показаны пунктиром на рис.
Реализация данного алгоритма достаточно проста. Для хранения максимальных значений y при каждом значении x используется массив, длина которого равна числу различимых точек (разрешению) по оси x в пространстве изображения. Значения, хранящиеся в этом массиве, представляют собой текущие значения "горизонта". Поэтому по мере рисования каждой очередной кривой этот горизонт "всплывает". Фактически этот алгоритм удаления невидимых линий работает каждый раз с одной линией.
Алгоритм работает очень хорошо до тех пор, пока какая-нибудь очередная кривая не окажется ниже самой первой из кривых, как показано на рис. а

Алгоритм плавающего горизонта
Подобные кривые, естественно, видимы и представляют собой нижнюю сторону исходной поверхности, однако алгоритм будет считать их невидимыми. Нижняя сторона поверхности делается видимой, если модифицировать этот алгоритм, включив в него нижний горизонт, который опускается вниз по ходу работы алгоритма.
Это реализуется при помощи второго массива, длина которого равна числу различимых точек по оси x в пространстве изображения.
Этот массив содержит наименьшие значения y для каждого значения x.
Алгоритм теперь становится таким: если на текущей плоскости при некотором заданном значении x соответствующее значение y на кривой больше максимума или меньше минимума по y для всех предыдущих кривых при этом значении x, то текущая кривая видима. В противном случае она невидима.
Полученный результат показан на рис. б.

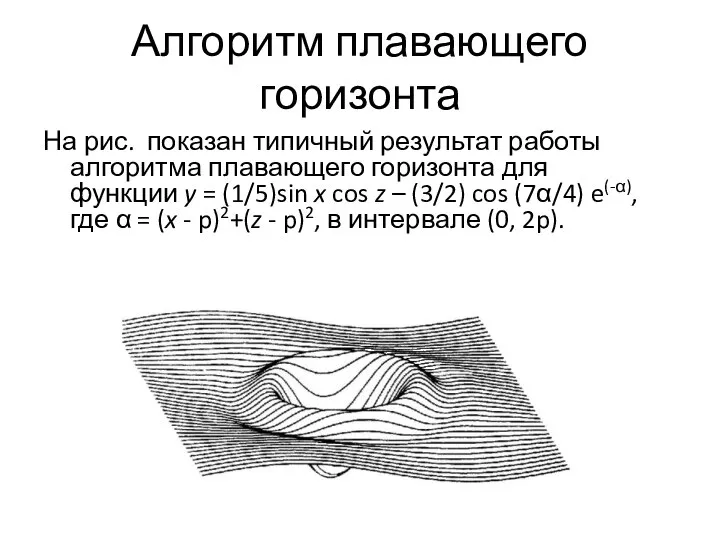
Алгоритм плавающего горизонта
На рис. показан типичный результат работы алгоритма плавающего горизонта для функции y = (1/5)sin x cos z – (3/2) cos (7α/4) e(-α), где α = (x - p)2+(z - p)2, в интервале (0, 2p).

Алгоритмы построчного сканирования для криволинейных поверхностей
Идея построчного сканирования, предложенная в 1967 г. Уайли, Ромни, Эвансом и Эрдалом, заключалась в том, что сцена обрабатывается в порядке прохождения сканирующей прямой.
В объектном пространстве это соответствует проведению секущей плоскости, перпендикулярной пространству изображения.
Строго говоря, алгоритм работает именно в пространстве изображения, отыскивая точки пересечения сканирующей прямой с ребрами многоугольников, составляющих картину (для случая изображения многогранников).
Но при пересечении очередного элемента рисунка выполняется анализ глубины полученной точки и сравнение ее с глубиной других точек на сканирующей плоскости.
В некоторых случаях можно построить список ребер, упорядоченный по глубине, но зачастую это невозможно выполнить корректно.
Поэтому сканирование сочетают с другими методами.