Содержание
- 2. Два муравья из муравейника должны добраться до пищи, которая находится за препятствием. Во время перемещения каждый
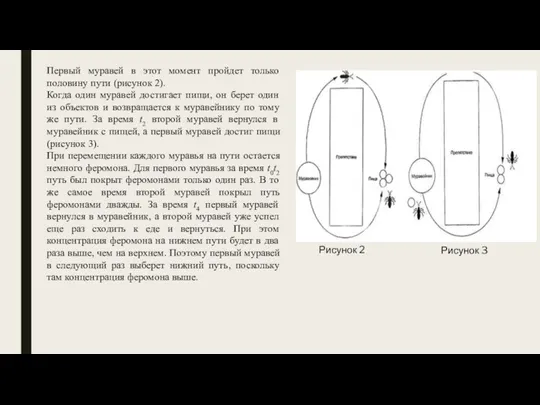
- 3. Первый муравей в этот момент пройдет только половину пути (рисунок 2). Когда один муравей достигает пищи,
- 4. Рисунок 4 – Блок-схема работы генетического алгоритма. Генетический алгоритм(ГА) и муравьиный алгоритм (Ant Colony System –
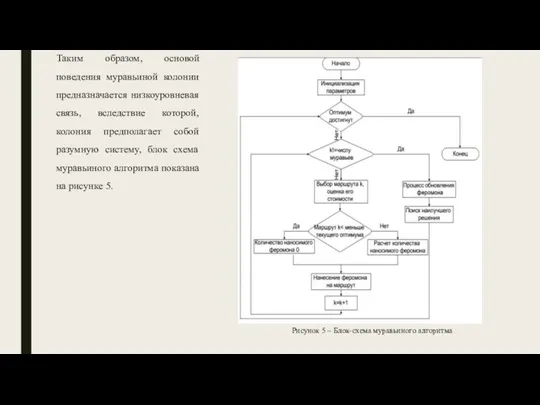
- 5. Таким образом, основой поведения муравьиной колонии предназначается низкоуровневая связь, вследствие которой, колония предполагает собой разумную систему,
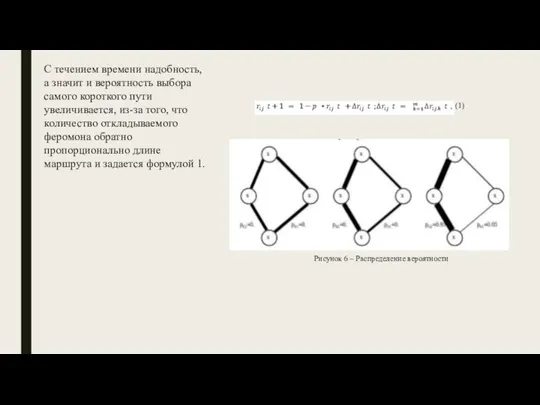
- 6. С течением времени надобность, а значит и вероятность выбора самого короткого пути увеличивается, из-за того, что
- 7. Реализация муравьиного алгоритма на примере задачи коммивояжера Задан взвешенный граф G1 (рисунок 7). Найти длину пути
- 8. В начале движения из вершины 1 муравей имеет четыре возможных пути: в вершину 2, 3, 4
- 9. Остается запустить генератор случайных чисел и узнать, куда попадает случайное число. В нашем случае генератор дает
- 10. Случайное число =61, полученное генератором случайных чисел попадает на второй участок. Этот участок указывает на вершину
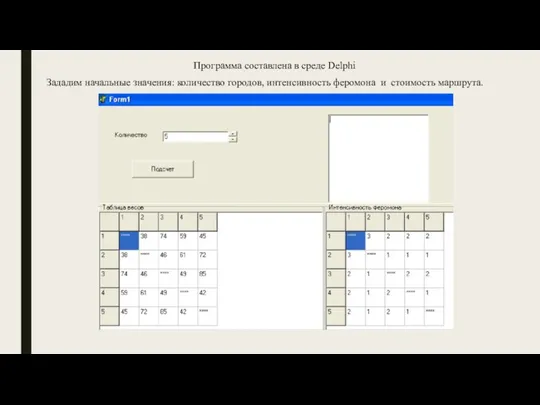
- 11. Программа составлена в среде Delphi Зададим начальные значения: количество городов, интенсивность феромона и стоимость маршрута.
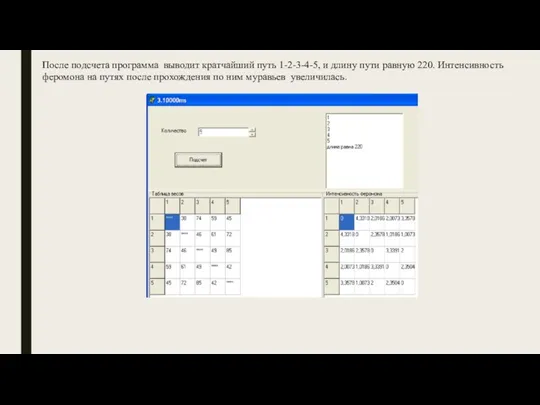
- 12. После подсчета программа выводит кратчайший путь 1-2-3-4-5, и длину пути равную 220. Интенсивность феромона на путях
- 13. В ходе вычислительного эксперимента были сравнены решения данной задачи с помощью муравьиного и генетического алгоритмов. В
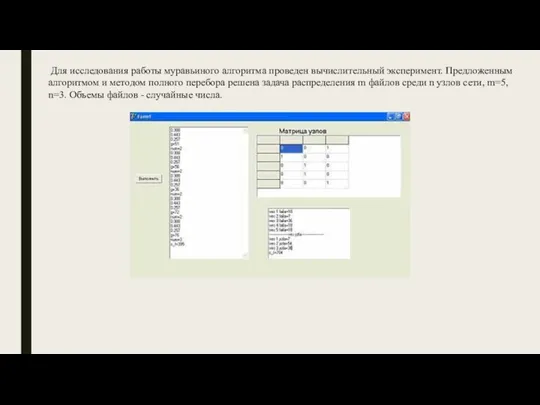
- 14. Для исследования работы муравьиного алгоритма проведен вычислительный эксперимент. Предложенным алгоритмом и методом полного перебора решена задача
- 16. Скачать презентацию







 Алгоритмы и алгостихи
Алгоритмы и алгостихи Разработка сайта для привлечения молодежи к культуре тюркоязычного коренного народа
Разработка сайта для привлечения молодежи к культуре тюркоязычного коренного народа Презентация на тему Что такое программирование 9 класс
Презентация на тему Что такое программирование 9 класс  Роль материаловедения в графическом дизайне
Роль материаловедения в графическом дизайне Использование интернет-платформ в период дистанционного обучения
Использование интернет-платформ в период дистанционного обучения Мастерская записи и обработки звука Прямой эфир
Мастерская записи и обработки звука Прямой эфир Авторитарный протокол в сетевых боевиках
Авторитарный протокол в сетевых боевиках Статистическая обработка данных
Статистическая обработка данных Моделирование как метод познания
Моделирование как метод познания GET и POST запросы в MVC5
GET и POST запросы в MVC5 Вселенная коллекционера
Вселенная коллекционера Нанотехнологии в информатике
Нанотехнологии в информатике Федеральный мобильный гид по экообъектам, услугам и мероприятиям
Федеральный мобильный гид по экообъектам, услугам и мероприятиям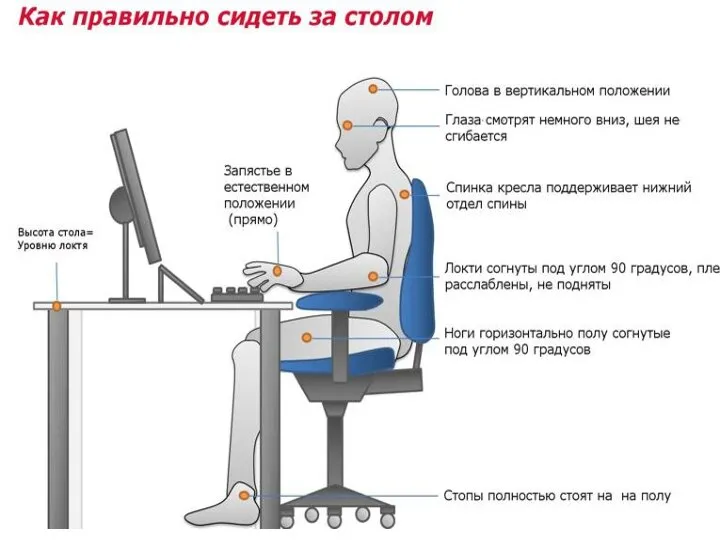 Как правильно сидеть за компьютером
Как правильно сидеть за компьютером Кооперация процессов и основные аспекты её логической организации
Кооперация процессов и основные аспекты её логической организации Привилегии баз данных
Привилегии баз данных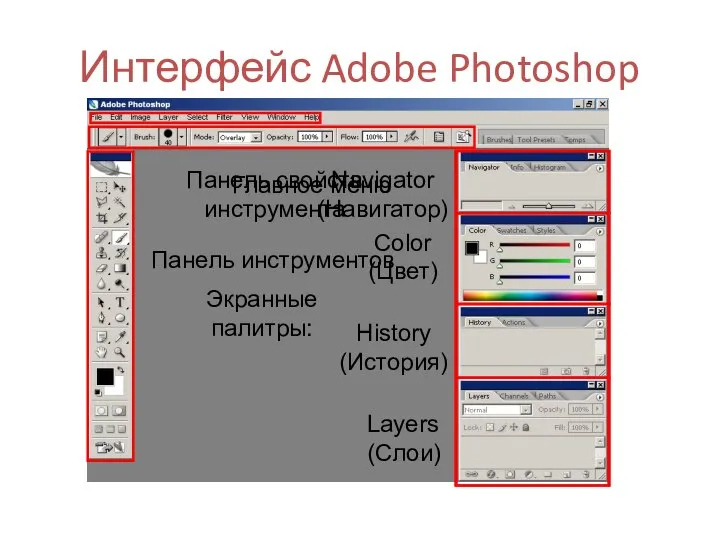 Интерфейс Adobe Photoshop
Интерфейс Adobe Photoshop Классификации ПО. Общие сведения
Классификации ПО. Общие сведения Внешние и внутренние компоненты ПК. Тема 13
Внешние и внутренние компоненты ПК. Тема 13 Курс Базы данных
Курс Базы данных Методы массивов. Метод массива splice
Методы массивов. Метод массива splice Введение в язык С
Введение в язык С Мониторинг деятельности классного коллектива средствами школьного СМИ
Мониторинг деятельности классного коллектива средствами школьного СМИ Debian. Выпуски Debian
Debian. Выпуски Debian Базіка - сервіс чат ботів
Базіка - сервіс чат ботів Двумерные массивы
Двумерные массивы Microprocessor-Based Systems
Microprocessor-Based Systems Возможности текстового процессора WORD
Возможности текстового процессора WORD