Общая постановка и алгоритм решения задач динамического программирования. Тема 1.5

Динамическое программирование – раздел математического программирования, совокупность приемов, позволяющих находить оптимальные решения, основанные на вычислении последствий каждого решения и выработке оптимальной стратегии для последующих решений

Процессы принятия решений, которые строятся по такому принципу, называются многошаговыми процессами

Динамическое программирование (иначе «динамическое планирование») – это особый метод оптимизации решений, специально приспособленный к «многошаговым» операциям.

Динамическое программирование позволяет свести одну сложную задачу со многими переменными ко многим задачам с малым числом переменных.
Это значительно сокращает объем вычислений и ускоряет процесс принятия управленческого решения.

Постановка задачи
Рассмотрим операцию Q, состоящую из m шагов (этапов). Пусть эффективность операции характеризуется каким-то показателем W, который называется «выигрышем».
Предположим, что выигрыш W за всю операцию складывается из выигрышей на отдельных шагах:
где wi — выигрыш на i-м шаге.
Если W обладает таким свойством, то его называют «аддитивным критерием».

Операция Q представляет собой управляемый процесс, т. е. можно выбирать какие-то параметры, влияющие на его ход и исход, причем на каждом шаге выбирается какое-то решение, от которого зависит выигрыш на данном шаге и выигрыш за операцию в целом.
Это решение называется «шаговым управлением».
Совокупность всех шаговых управлений представляет собой управление операцией в целом. Обозначим его буквой х, а шаговые управления — буквами х1, х2, ..., xm:
x = (х1, х2, ..., xm)

Требуется найти такое управление x*, при котором выигрыш W обращается в максимум:
То управление x*, при котором этот максимум достигается, будем называть оптимальным управлением. Оно состоит из совокупности оптимальных шаговых управлений:
x* = (х*1, х*2, ..., x*m)
и позволяет достигнуть максимальный выигрыш W*.

Оптимальное распределение ресурсов
Пусть имеется некоторое количество ресурсов х, которое необходимо распределить между n различными предприятиями, объектами, работами и т.д. так, чтобы получить максимальную суммарную эффективность от выбранного способа распределения.

Оптимальное распределение ресурсов
Введем обозначения: xi — количество ресурсов, выделенных i-му предприятию;
gi(xi) — функция полезности, в данном случае это величина дохода от использования ресурса xi, полученного i-м предприятием;
fk(x) — наибольший доход, который можно получить при использовании ресурсов х от первых k различных предприятий.

Оптимальное распределение ресурсов
Математическая форма

Оптимальное распределение ресурсов
Для решения задачи необходимо получить рекуррентное соотношение, связывающее fk(x) и fk-1(x).
Обозначим через хk количество ресурса, используемого k-м способом (0 ≤ xk ≤ х), тогда для (k — 1) способов остается величина ресурсов, равная (x — xk). Наибольший доход, который получается при использовании ресурса (x — xk) от первых (k — 1) способов, составит
fk-1(x — xk).

Оптимальное распределение ресурсов
Для максимизации суммарного дохода от k-гo и первых (k — 1) способов необходимо выбрать xk таким образом, чтобы выполнялись соотношения

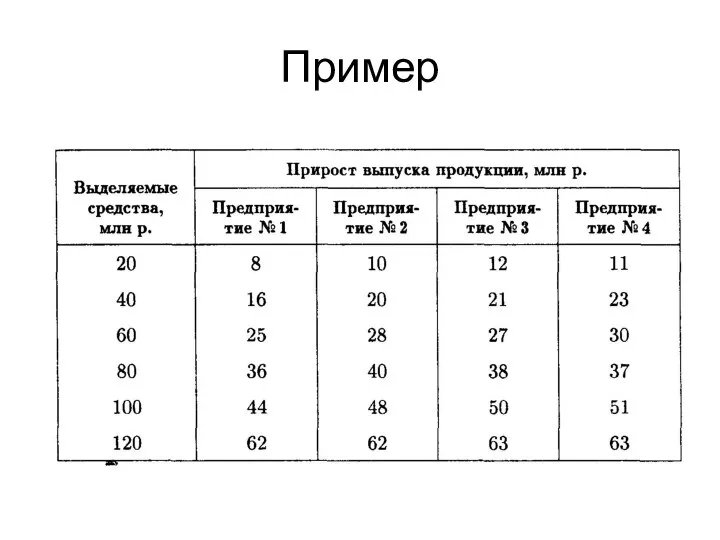
Пример
Совет директоров фирмы рассматривает предложения по наращиванию производственных мощностей для увеличения выпуска однородной продукции на четырех предприятиях, принадлежащих фирме.
Для расширения производства совет директоров выделяет средства в объеме 120 млн р. с дискретностью 20 млн р. Прирост выпуска продукции на предприятиях зависит от вы­деленной суммы, его значения представлены предприятиями и содержатся в таблице
Найти распределение средств между предприятиями, обеспечивающее максимальный прирост выпуска продукции, причем на одно предприятие можно осуществить не более одной инвестиции.

Пример

Решение
Разобьем решение задачи на четыре этапа по количеству предприятий, на которых предполагается осуществить инвестиции.

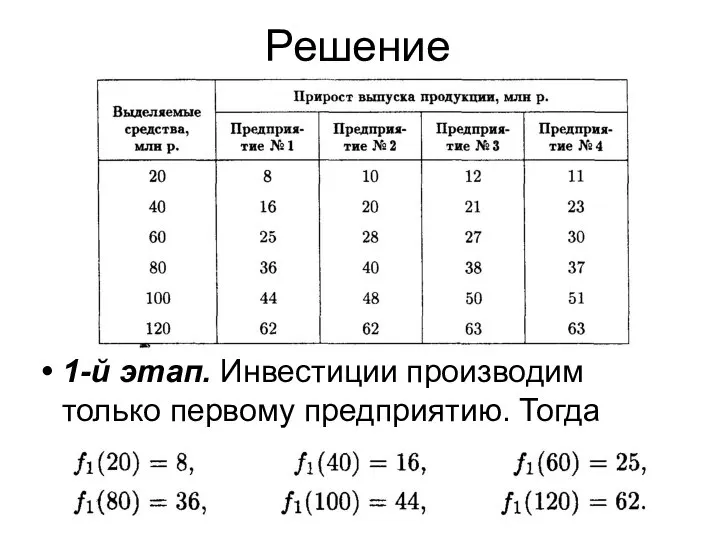
Решение
1-й этап. Инвестиции производим только первому предприятию. Тогда

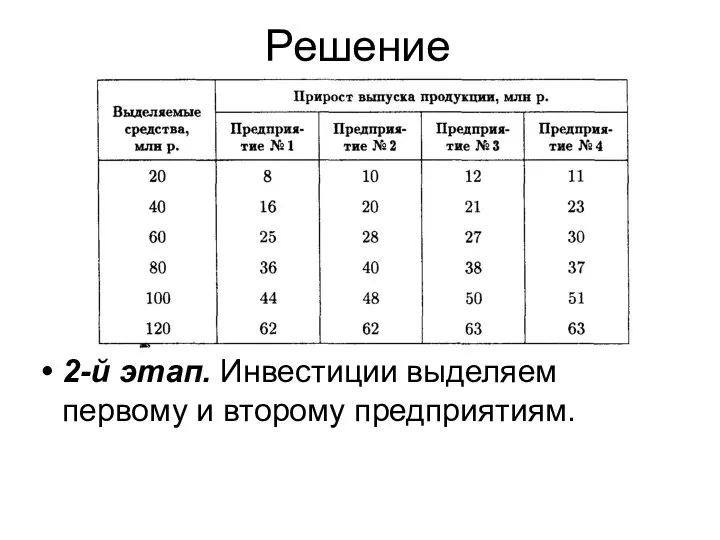
Решение
2-й этап. Инвестиции выделяем первому и второму предприятиям.

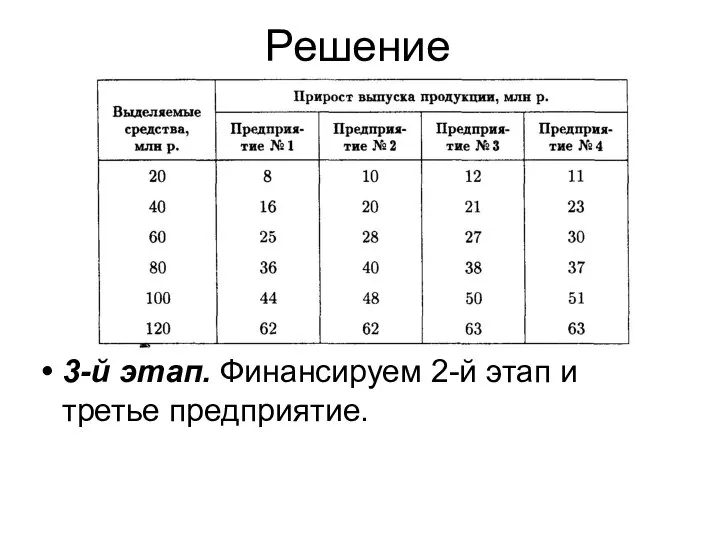
Решение
3-й этап. Финансируем 2-й этап и третье предприятие.

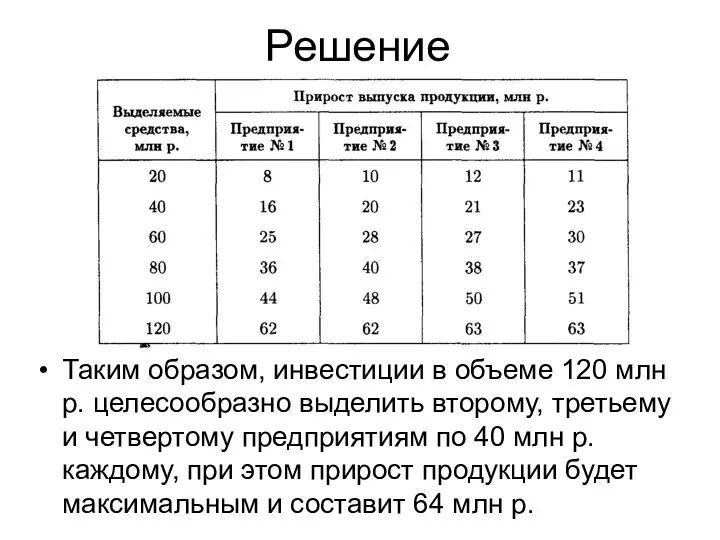
Решение
4-й этап. Инвестиции в объеме 120 млн р. распределяем между 3-м этапом и четвертым предприятием.

Решение
Получены условия управления от 1-го до 4-го этапа. Вернемся от 4-го к 1-му этапу.

Решение
Таким образом, инвестиции в объеме 120 млн р. целесообразно выделить второму, третьему и четвертому предприятиям по 40 млн р. каждому, при этом прирост продукции будет максимальным и составит 64 млн р.

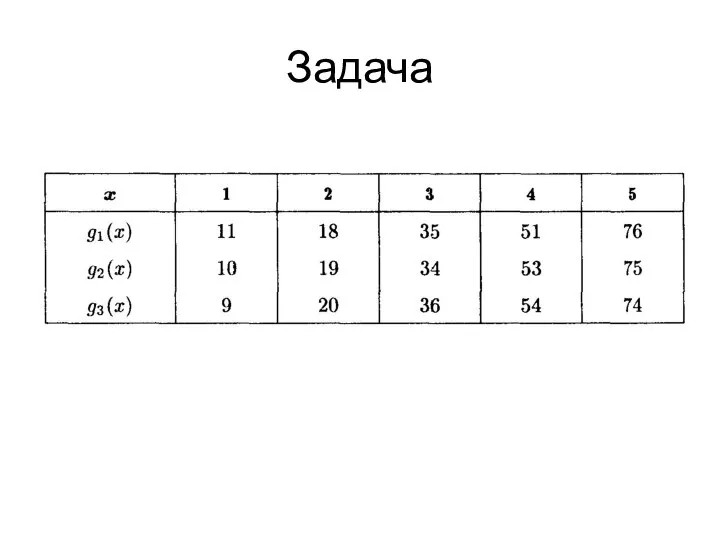
Задача
В трех районах города предприниматель планирует построить пять предприятий одинаковой мощности по выпуску хлебобулочных изделий, пользующихся спросом.
Необходимо разместить предприятия таким образом, чтобы обеспечить минимальные суммарные затраты на их строительство и эксплуатацию. Значения функции затрат gi(x) приведены в таблице

Задача

Оптимальная стратегия замены оборудования
Оптимальная стратегия замены оборудования состоит в определении оптимальных сроков замены.
Критерием оптимальности может служить прибыль от эксплуатации оборудования, которую следует оптимизировать, или суммарные затраты на эксплуатацию в течение рассматриваемого промежутка времени, подлежащие минимизации.