Сортировка одномерных массивов

Определение
Алгоритмом сортировки называется алгоритм для упорядочения некоторого множества элементов.
Обычно под алгоритмом сортировки подразумевают алгоритм упорядочивания множества элементов по возрастанию или убыванию.

Определение
В случае наличия элементов с одинаковыми значениями, в упорядоченной последовательности они располагаются рядом друг за другом в любом порядке.
Однако иногда бывает полезно сохранять первоначальный порядок элементов с одинаковыми значениями.

Определение
В алгоритмах сортировки лишь часть данных используется в качестве ключа сортировки.
Ключом сортировки называется атрибут (или несколько атрибутов), по значению которого определяется порядок элементов. Таким образом, при написании алгоритмов сортировок массивов следует учесть, что ключ полностью или частично совпадает с данными.

Определение
Практически каждый алгоритм сортировки можно разбить на 3 части:
сравнение, определяющее упорядоченность пары элементов;
перестановку, меняющую местами пару элементов;
сортирующий алгоритм, который осуществляет сравнение и перестановку элементов до тех пор, пока все элементы множества не будут упорядочены.

Определение
Алгоритмы сортировки имеют большое практическое применение.
Их можно встретить там, где речь идет об обработке и хранении больших объемов информации.
Некоторые задачи обработки данных решаются проще, если данные заранее упорядочить.

Оценка алгоритмов сортировки
Ни одна другая проблема не породила такого количества разнообразнейших решений, как задача сортировки.
Универсального, наилучшего алгоритма сортировки на данный момент не существует.

Оценка алгоритмов сортировки
Однако, имея приблизительные характеристики входных данных, можно подобрать метод, работающий оптимальным образом.
Для этого необходимо знать параметры, по которым будет производиться оценка алгоритмов.

Оценка алгоритмов сортировки
Время сортировки – основной параметр, характеризующий быстродействие алгоритма.
Устойчивость – это параметр, который отвечает за то, что сортировка не меняет взаимного расположения равных элементов.

Оценка алгоритмов сортировки
Память – один из параметров, который характеризуется тем, что ряд алгоритмов сортировки требуют выделения дополнительной памяти под временное хранение данных.
При оценке используемой памяти не будет учитываться место, которое занимает исходный массив данных и независящие от входной последовательности затраты, например, на хранение кода программы.

Оценка алгоритмов сортировки
Естественность поведения – параметр, которой указывает на эффективность метода при обработке уже отсортированных, или частично отсортированных данных. Алгоритм ведет себя естественно, если учитывает эту характеристику входной последовательности и работает лучше.

Классификация алгоритмов сортировок
Все разнообразие и многообразие алгоритмов сортировок можно классифицировать по различным признакам, например, по устойчивости, по поведению, по использованию операций сравнения, по потребности в дополнительной памяти, по потребности в знаниях о структуре данных, выходящих за рамки операции сравнения, и другие.

Классификация алгоритмов сортировок
Рассмотрим классификацию алгоритмов сортировки по сфере применения:
Внутренняя сортировка
Внешняя сортировка

Классификация алгоритмов сортировок
Внутренняя сортировка – это алгоритм сортировки, который в процессе упорядочивания данных использует только оперативную память (ОЗУ) компьютера.
То есть оперативной памяти достаточно для помещения в нее сортируемого массива данных с произвольным доступом к любой ячейке и собственно для выполнения алгоритма.

Классификация алгоритмов сортировок
Внутренняя сортировка применяется во всех случаях, за исключением однопроходного считывания данных и однопроходной записи отсортированных данных.
В зависимости от конкретного алгоритма и его реализации данные могут сортироваться в той же области памяти, либо использовать дополнительную оперативную память.

Классификация алгоритмов сортировок
Внешняя сортировка – это алгоритм сортировки, который при проведении упорядочивания данных использует внешнюю память, как правило, жесткие диски.
Внешняя сортировка разработана для обработки больших списков данных, которые не помещаются в оперативную память.

Классификация алгоритмов сортировок
Обращение к различным носителям накладывает некоторые дополнительные ограничения на данный алгоритм: доступ к носителю осуществляется последовательным образом, то есть в каждый момент времени можно считать или записать только элемент, следующий за текущим; объем данных не позволяет им разместиться в ОЗУ.

Классификация алгоритмов сортировок
Внутренняя сортировка является базовой для любого алгоритма внешней сортировки – отдельные части массива данных сортируются в оперативной памяти и с помощью специального алгоритма сцепляются в один массив, упорядоченный по ключу.

Классификация алгоритмов сортировок
Следует отметить, что внутренняя сортировка значительно эффективней внешней, так как на обращение к оперативной памяти затрачивается намного меньше времени, чем к носителям.

Глупая сортировка
Просматриваем массив слева-направо и по пути сравниваем соседей.
Если мы встретим пару взаимно неотсортированных элементов, то меняем их местами и возвращаемся в самое начало массива. Снова проходим-проверяем массив, если встретили снова «неправильную» пару соседних элементов, то меняем местами и опять начинаем всё снова. Продолжаем до тех пор пока происходит обмен элементов.

Глупая сортировка
Пример работы алгоритма:

Глупая сортировка

Пузырьковая сортировка
Сортировка простыми обменами, сортировка пузырьком (англ. bubble sort) — простой алгоритм сортировки.
Для понимания и реализации этот алгоритм — простейший, но эффективен он лишь для небольших массивов.

Пузырьковая сортировка
Алгоритм считается учебным и практически не применяется вне учебной литературы, вместо него на практике применяются более эффективные алгоритмы сортировки.
Алгоритм состоит из повторяющихся проходов по сортируемому массиву.

Пузырьковая сортировка
Пример работы алгоритма:

Пузырьковая сортировка
Обходим массив от начала до конца, попутно меняя местами неотсортированные соседние элементы.
В результате первого прохода на последнее место «всплывёт» максимальный элемент.

Пузырьковая сортировка
Теперь снова обходим неотсортированную часть массива (от первого элемента до предпоследнего) и меняем по пути неотсортированных соседей. Второй по величине элемент окажется на предпоследнем месте.

Пузырьковая сортировка
Продолжая также далее, будем обходить всё уменьшающуюся неотсортированную часть массива, помещая найденные максимумы в конец.

Пузырьковая сортировка

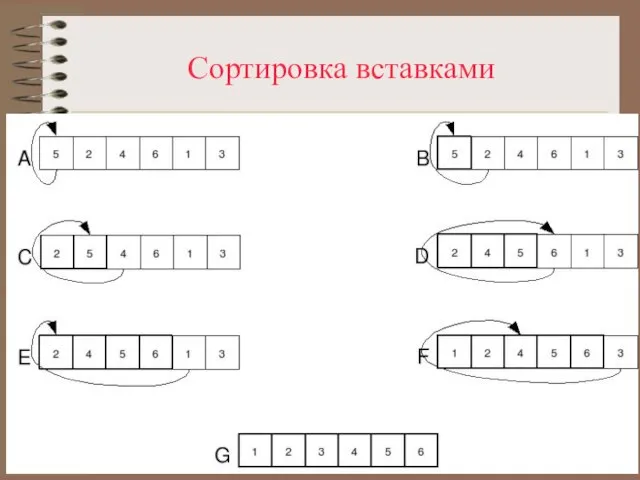
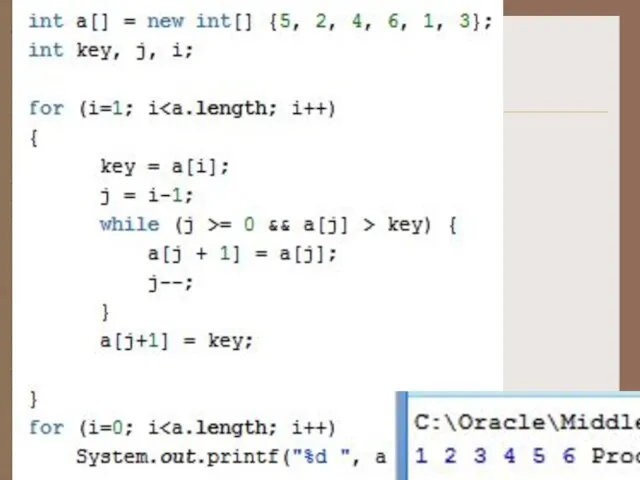
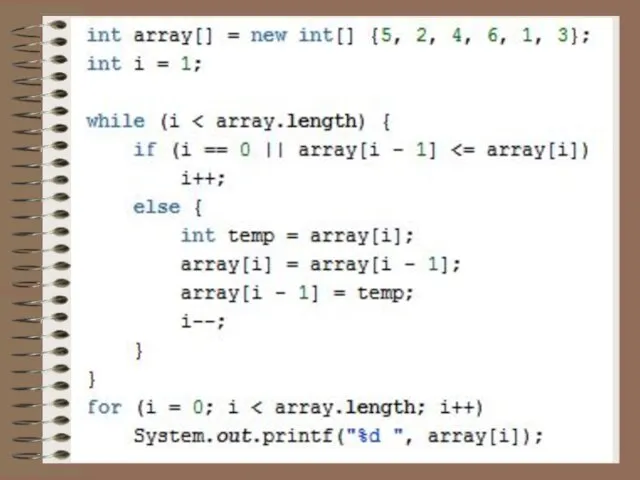
Сортировка вставками
Сортировка вставками (англ. Insertion sort) — алгоритм сортировки, в котором элементы входной последовательности просматриваются по одному, и каждый новый поступивший элемент размещается в подходящее место среди ранее упорядоченных элементов.

Сортировка вставками

Сортировка вставками

Сортировка вставками

Шейкерная сортировка
Сортировка перемешиванием, или Шейкерная сортировка, или двухсторонней сортировкой простыми обменами (англ. Cocktail sort) — разновидность пузырьковой сортировки.

Шейкерная сортировка
Производится многократный прогон по массиву, соседние элементы сравниваются и, в случае необходимости, меняются местами. При достижении конца массива направление меняется на противоположное. Таким образом по очереди выталкиваются крупные и мелкие элементы массива в конец и начало структуры соответственно.

Шейкерная сортировка

Шейкерная сортировка

Сортировка чёт-нечет
Этот относительно простой алгоритм сортировки является модификацией пузырьковой сортировки.
Суть модификации в том, чтобы сравнивать элементы массива под чётными и нечётными индексами с последующими элементами независимо.
Алгоритм был впервые представлен Н. Хаберманом (N. Haberman) в 1972 году.

Сортировка чёт-нечет
Заводится флаг, определяющий отсортирован ли массив. В начале итерации ставится в состояние «истина», далее каждый нечётный элемент сверяется с последующим и если они стоят в не правильном порядке (предыдущий больше следующего), то они меняются местами, и флаг ставится в состояние «ложь». То же самое делается с чётными элементами. Алгоритм не прекращает работу, пока флаг не останется в состоянии «истина».

Сортировка чёт-нечет

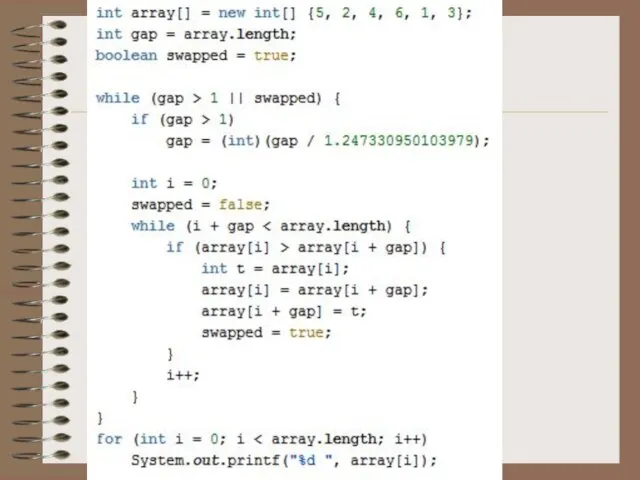
Сортировка чёт-нечет

Сортировка расчёской
Сортировка расчёской (англ. comb sort) — это довольно упрощённый алгоритм сортировки, изначально спроектированный Влодзимежом Добосевичем в 1980г. Позднее он был переоткрыт и популяризован в статье Стивена Лэйси и Ричарда Бокса в журнале Byte Magazine в апреле 1991г

Сортировка расчёской
В «пузырьке», «шейкере» и «чёт-нечете» при переборе массива сравниваются соседние элементы.
Основная идея «расчёски» в том, чтобы первоначально брать достаточно большое расстояние между сравниваемыми элементами и по мере упорядочивания массива сужать это расстояние вплоть до минимального.

Сортировка расчёской
Таким образом, мы как бы причёсываем массив, постепенно разглаживая на всё более аккуратные пряди.

Сортировка расчёской
Первоначальный разрыв между сравниваемыми элементами лучше брать с учётом специальной величины, называемой фактором уменьшения, оптимальное значение которой равно примерно 1,247.
где е - экспонента; φ - "золотое" число

Сортировка расчёской
Сначала расстояние между элементами равно размеру массива, разделённого на фактор уменьшения (результат округляется до ближайшего целого).
Затем, пройдя массив с этим шагом, необходимо поделить шаг на фактор уменьшения и пройти по списку вновь.

Сортировка расчёской
Так продолжается до тех пор, пока разность индексов не достигнет единицы. В этом случае массив досортировывается обычным пузырьком.

Сортировка расчёской

Сортировка расчёской

Гномья сортировка
Гномья сортировка (англ. Gnome sort) — алгоритм сортировки, похожий на сортировку вставками, но в отличие от последней перед вставкой на нужное место происходит серия обменов, как в сортировке пузырьком.

Гномья сортировка
Алгоритм находит первое место, где два соседних элемента стоят в неправильном порядке и меняет их местами.
Он пользуется тем фактом, что обмен может породить новую пару, стоящую в неправильном порядке, только до или после переставленных элементов.

Гномья сортировка
Он не допускает, что элементы после текущей позиции отсортированы, таким образом, нужно только проверить позицию до переставленных элементов.

Гномья сортировка

Гномья сортировка

Методы внешней сортировки
Внешняя сортировка – это сортировка данных, которые расположены на внешних устройствах и не вмещаются в оперативную память.
К наиболее известным алгоритмам внешних сортировок относятся:
сортировки слиянием (простое и естественное слияние);
улучшенные сортировки (многофазная и каскадная сортировка).

Методы внешней сортировки
Из представленных внешних сортировок наиболее важным является метод сортировки с помощью слияния.
Серия (упорядоченный отрезок) – это последовательность элементов, которая упорядочена по ключу.

Методы внешней сортировки
Количество элементов в серии называется длиной серии.
Серия, состоящая из одного элемента, упорядочена всегда. Последняя серия может иметь длину меньшую, чем остальные серии файлов.
Максимальное количество серий в файле N (все элементы не упорядочены).
Минимальное количество серий одна (все элементы упорядочены).

Методы внешней сортировки
Слияние – это процесс объединения двух (или более) упорядоченных серий в одну упорядоченную последовательность при помощи циклического выбора элементов, доступных в данный момент.
Распределение – это процесс разделения упорядоченных серий на два и несколько вспомогательных файла.

Методы внешней сортировки
Фаза – это действия по однократной обработке всей последовательности элементов.
Двухфазная сортировка – это сортировка, в которой отдельно реализуется две фазы: распределение и слияние.
Однофазная сортировка – это сортировка, в которой объединены фазы распределения и слияния в одну.

Методы внешней сортировки
Двухпутевым слиянием называется сортировка, в которой данные распределяются на два вспомогательных файла.
Многопутевым слиянием называется сортировка, в которой данные распределяются на N (N>2) вспомогательных файлов.

Общий алгоритм сортировки слиянием
Сначала серии распределяются на два или более вспомогательных файлов. Данное распределение идет поочередно: первая серия записывается в первый вспомогательный файл, вторая – во второй и так далее до последнего вспомогательного файла.
Затем опять запись серии начинается в первый вспомогательный файл.

Общий алгоритм сортировки слиянием
После распределения всех серий, они объединяются в более длинные упорядоченные отрезки, то есть из каждого вспомогательного файла берется по одной серии, которые сливаются.
Если в каком-то файле серия заканчивается, то переход к следующей серии не осуществляется.

Общий алгоритм сортировки слиянием
В зависимости от вида сортировки сформированная более длинная упорядоченная серия записывается либо в исходный файл, либо в один из вспомогательных файлов. После того как все серии из всех вспомогательных файлов объединены в новые серии, потом опять начинается их распределение.
И так до тех пор, пока все данные не будут отсортированы.

Общий алгоритм сортировки слиянием
Основные характеристики сортировки слиянием:
количество фаз в реализации сортировки;
количество вспомогательных файлов, на которые распределяются серии.

Сортировка простым слиянием
В данном алгоритме длина серий фиксируется на каждом шаге.
В исходном файле все серии имеют длину 1, после первого шага она равна 2, после второго – 4, после третьего – 8, после k -го шага – 2k.

Сортировка простым слиянием
Алгоритм сортировки простым слиянием
Шаг 1. Исходный файл f разбивается на два вспомогательных файла f1 и f2.
Шаг 2. Вспомогательные файлы f1 и f2 сливаются в файл f, при этом одиночные элементы образуют упорядоченные пары.

Сортировка простым слиянием
Шаг 3. Полученный файл f вновь обрабатывается, как указано в шагах 1 и 2. При этом упорядоченные пары переходят в упорядоченные четверки.
Шаг 4. Повторяя шаги, сливаем четверки в восьмерки и т.д., каждый раз удваивая длину слитых последовательностей до тех пор, пока не будет упорядочен целиком весь файл.

Сортировка простым слиянием
Признаками конца сортировки простым слиянием являются следующие условия:
длина серии не меньше количества элементов в файле (определяется после фазы слияния);
количество серий равно 1 (определяется на фазе слияния).
при однофазной сортировке второй по счету вспомогательный файл после распределения серий остался пустым.

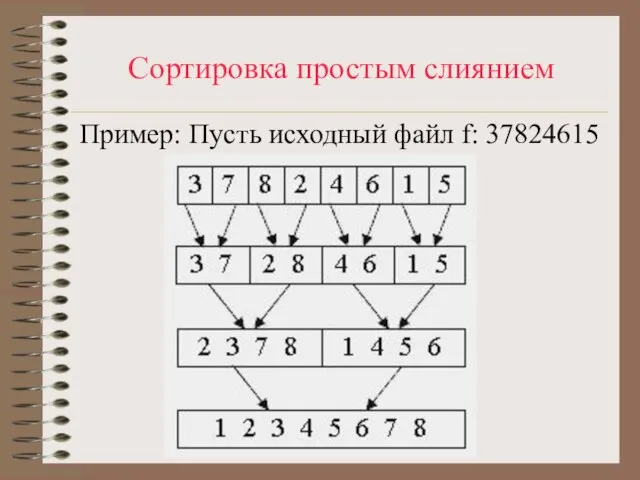
Сортировка простым слиянием

Сортировка простым слиянием
Пример: Пусть исходный файл f: 37824615

Алгоритм сортировки естественным слиянием
Шаг 1. Исходный файл f разбивается на два вспомогательных файла f1 и f2. Распределение происходит следующим образом: поочередно считываются записи ai исходной последовательности (неупорядоченной) таким образом, что если значения ключей соседних записей удовлетворяют условию f(ai) <= f(ai+1), то они записываются в первый вспомогательный файл f1.

Алгоритм сортировки естественным слиянием
Как только встречаются f(ai) > f(ai+1), то записи ai+1 копируются во второй вспомогательный файл f2.
Процедура повторяется до тех пор, пока все записи исходной последовательности не будут распределены по файлам.

Алгоритм сортировки естественным слиянием
Шаг 2. Вспомогательные файлы f1 и f2 сливаются в файл f, при этом серии образуют упорядоченные последовательности.
Шаг 3. Полученный файл f вновь обрабатывается, как указано в шагах 1 и 2.
Шаг 4. Повторяя шаги, сливаем упорядоченные серии до тех пор, пока не будет упорядочен целиком весь файл.

Алгоритм сортировки естественным слиянием
Символ "`" обозначает признак конца серии.
Признаками конца сортировки естественным слиянием являются следующие условия:
количество серий равно 1 (определяется на фазе слияния).
при однофазной сортировке второй по счету вспомогательный файл после распределения серий остался пустым.

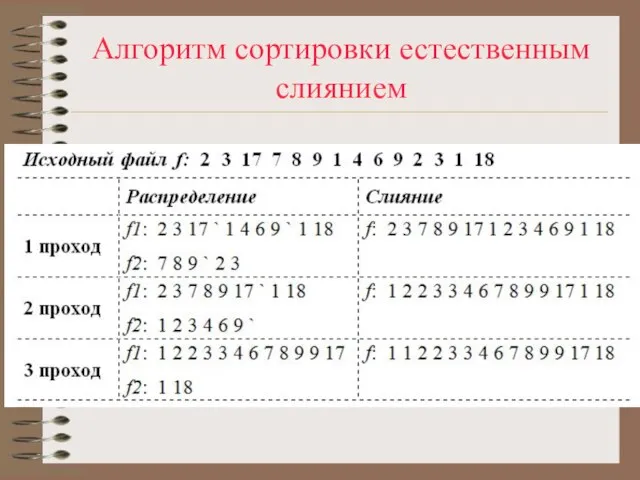
Алгоритм сортировки естественным слиянием
Естественное слияние, у которого после фазы распределения количество серий во вспомогательных файлах отличается друг от друга не более чем на единицу, называется сбалансированным слиянием, в противном случае – несбалансированное слияние.

Алгоритм сортировки естественным слиянием