Основные понятия векторной графики

Теория
Векторная графика является способом представления изображений, основанном на математическом описании элементарных геометрических объектов, называемых примитивами. В качестве примитивов выступают точки, линии, сплайны, кривые Безье, круги и окружности, многоугольники.

Изображение, созданное в векторных программах, основывается на математических формулах, а не на координатах пикселов. Поэтому векторные файлы содержат наборы инструкций для построения геометрических объектов.
Основу векторных изображений составляют разнообразные линии, называемые векторами, или контурами.
Каждый контур представляет собой независимый объект, который можно редактировать: перемещать, масштабировать, изменять.

Достоинства
Небольшой размер файла при относительно несложной детализации изображения.
Возможность неограниченного масштабирования без потери качества.
Возможность перемещения, вращения, растягивания, группировки и т.д.так же без потери качества.
Возможность позиционирования объектов по оси, перпендикулярной плоскости экрана (по оси z — «выше», «ниже», «выше всех», «ниже всех»).
Возможность выполнения булевых преобразований над объектами — сложение, вычитание, пересечение, дополнение.
Управление толщиной линий при любом масштабе изображения.

Недостатки
Большой размер файла при сложной детализации изображения. (Бывают случаи, что из‑за множства мелких сложных деталей размер векторного изображения гораздо превышает размер его растровой копии)
Трудность передачи фотореалистичного изображения (следует из 1‑го недостатка)
Проблемы совместимости программ, работающих с векторной графикой, при этом не все программы открывают (или корректно отображают) даже «общепринятые» форматы (такие как eps), созданные в других редакторах.

Форматы
SVGSVG;CDRSVG;CDR;CGMSVG;CDR;CGM;DXFSVG;CDR;CGM;DXF;OpenVGSVG;CDR;CGM;DXF;OpenVG;GXLSVG;CDR;CGM;DXF;OpenVG;GXL;WMF;
EPSEPS;PDFEPS;PDF;AI

Примеры

Векторные изображения могут быть созданы несколькими видами программ:
- Программы векторной графики (например, CorelDRAW, Inkscape);
- Программы САПР (системы автоматизированного проектирования; типичным представителем является программа AutoCAD);
- Специализированные программы конвертирования растровых изображений в векторные.

Векторные редакторы и программы САПР являются наиболее эффективным средством для построения шрифтовых и высокоточных графических объектов, таких как, например, конструкторские чертежи.
Для таких изображений принципиальное значение имеет сохранение четких контуров вне зависимости от исходных размеров изображения и масштабирования.

При выводе изображения, созданного в векторной программе, качество результата не зависит от исходного разрешения изображения, а определяется лишь разрешающей способностью устройств вывода (монитора, принтера, плоттера и т.д.).
Благодаря тому, что качество векторного изображения не связано с разрешением, файлы векторных изображений имеют, как правило, меньший объем по сравнению с файлами растровых изображений

Отличия механизмов формирования изображений в растровой и
векторной графике
Проиллюстрировать разницу в механизмах работы растровых и векторных редакторов можно на примере описания одного и того же отрезка прямой.
В векторном формате задаются координаты начала и конца отрезка, а также цвет и толщина линии. Для сохранения такой информации на диске потребуется всего несколько байтов памяти.

В растровом формате необходимо задать координаты и цвет каждой точки (пиксела), входящей в этот отрезок прямой.
Поскольку количество входящих в нее пикселов зависит от разрешения, объем информации, необходимой для описания отрезка прямой (а значит, и требуемый для ее сохранения объем памяти), будет определяться установленным разрешением.

Структура векторного изображения
Структуру векторного изображения можно представить в виде иерархического дерева. В такой схеме готовая иллюстрация занимает верхний уровень, а ее составные части – более низкие уровни. Готовая иллюстрация, занимающая верхний иерархический уровень, объединяет в своем составе объекты, узлы, линии и заливки

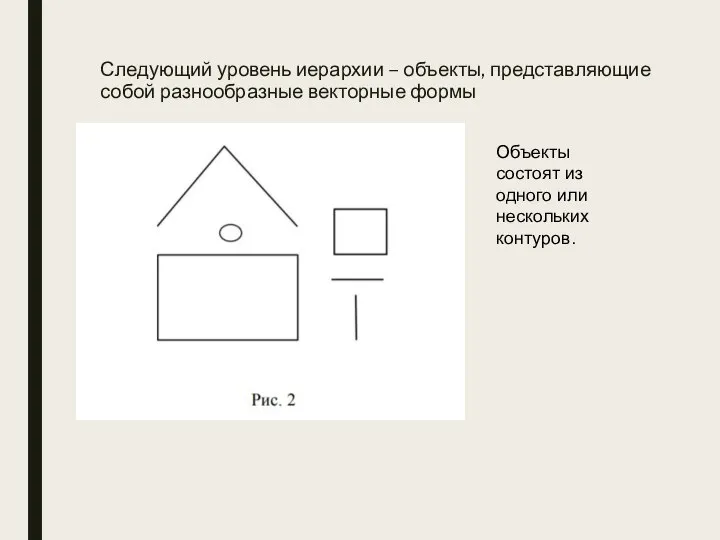
Следующий уровень иерархии – объекты, представляющие собой разнообразные векторные формы
Объекты состоят из одного или нескольких контуров.

Контур - Это любая геометрическая фигура, созданная с помощью рисующих инструментов векторной программы и представляющая собой очертания того или иного графического объекта.
Типичными примерами контуров могут служить окружность, прямоугольник, сегмент кривой линии и т.д.
Замкнутый контур — это замкнутая кривая, у которой начальная и конечная точки совпадают. Примером замкнутого контура является эллипс. Замкнутый контур также называют фигурой.
Открытый контур имеет четко обозначенные концевые точки. Синусоидальная линия, например, является открытым контуром.

Следующий уровень иерархии составляют сегменты, которые выполняют функции составных частей контуров.
Каждый контур может состоять из одного или нескольких сегментов. Начало и конец каждого сегмента называют узлами, или опорными точками, поскольку они фиксируют положение сегмента, привязывая его к определенной позиции в контуре.
Перемещение узловых точек приводит к модификации сегментов контура и к изменению его формы. Наряду с узлами в состав сегмента входят также линии (прямые или кривые), соединяющие между собой узлы.

Замкнутые контуры имеют свойство заливки, или заполнения цветом, текстурой или растровым изображением (картой).
Заливка – это цвет или узор, выводимый в замкнутой области, ограниченной кривой.
На самом нижнем уровне иерархии расположены узлы и отрезки линий, соединяющих между собой соседние узлы.
Линии наряду с узлами выполняют функции основных элементов векторного изображения.
Простейшая незамкнутая линия имеет две вершины, называемые узлами (или концевыми точками).

Математические основы векторной графики
Сегмент может быть задан с помощью уравнения прямой или уравнения кривой линии, требующих для своего описания разного количества параметров.
В векторной графике точке соответствует узел. На плоскости этот объект представляется двумя числами (x, y), задающими его положение относительно начала координат.

Прямая линия описывается уравнением
y=ax+b
Для построения данного объекта требуется задание всего двух параметров: а и b. Результатом будет построение бесконечной прямой в декартовых координатах.
В отличие от прямой, отрезок прямой требует для своего описания двух дополнительных параметров, соответствующих началу и концу отрезка.

К классу кривых второго порядка относятся параболы, гиперболы, эллипсы и окружности, то есть все линии, уравнения которых содержат переменные в степени не выше второй.
Кривые второго порядка не имеют точек перегиба. Используемое для описания этих кривых каноническое уравнение тр
ебует для своего задания пяти параметров:
Для построения отрезка кривой требуется задать два дополнительных
параметра.

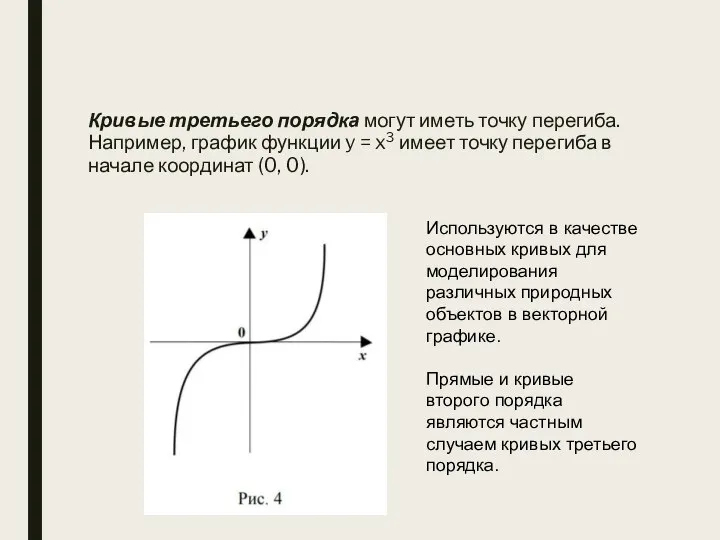
Кривые третьего порядка могут иметь точку перегиба. Например, график функции y = x3 имеет точку перегиба в начале координат (0, 0).
Используются в качестве основных кривых для моделирования различных природных объектов в векторной графике.
Прямые и кривые второго порядка являются частным случаем кривых третьего порядка.

Каноническое уравнение, используемое для описания кривой третьего порядка, требует для своего задания девяти параметров:
Для описания отрезка кривой третьего порядка требуется на два
параметра больше.
Важным для компьютерной графики частным случаем кривых третьего порядка являются уже встречавшиеся нам ранее кривые Безье. Эти кривые требуют для своего описания меньшего количества параметров – восьми вместо одиннадцати.

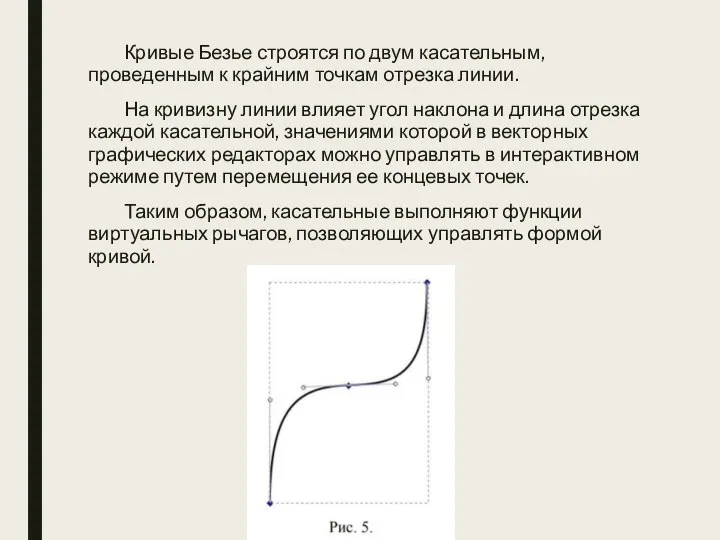
Кривые Безье строятся по двум касательным, проведенным к крайним точкам отрезка линии.
На кривизну линии влияет угол наклона и длина отрезка каждой касательной, значениями которой в векторных графических редакторах можно управлять в интерактивном режиме путем перемещения ее концевых точек.
Таким образом, касательные выполняют функции виртуальных рычагов, позволяющих управлять формой кривой.