Слайд 2Организационные моменты
Формат лекций
Формат экзамена
Бонусы:
- конспект
- посещения

Слайд 3О чем этот курс?
Общие сведения об алгоритмах
Основные элементы языка C++
Сложные типы данных

(массивы)
Распределения памяти, указатели
Функции
Алгоритмы поиска и сортировки
Работа со строками
Работа с файлами
Слайд 4Литература
C++:
Шилдт Г. Теория и практика C++
Страуструп Б. Язык программирования C++: специальное издание
Алгоритмы:
Томас

Кормен и др. Алгоритмы. Построение и анализ
Роберт Седжвик. Алгоритмы на C++
Кнут, Д.Э. Искусство программирования
Слайд 5Содержание лекции
Алгоритмы и их свойства
Способы записи алгоритмов
Базовые алгоритмические структуры
Величины в алгоритмах
Примеры

Слайд 6Этапы решения задач на ЭВМ
Постановка задачи
Формализация (математическая постановка)
Выбор (или разработка) метода решения
Разработка

алгоритма.
Составление программы
Отладка программы
Вычисление и обработка результатов.
Слайд 7Постановка задачи
определить цель и категорию программы (системная, прикладная)
определить исходные данные и требуемый

результат
проверить, является ли задача хорошо поставленной (должны быть определены все связи между исходными данными и результатом)
зафиксировать требования к программе в письменной форме
Слайд 8Формализация
все объекты задачи описываются на языке математики
выбираются математические абстракции, адекватно, то есть

с требуемой точностью и полнотой, представляющие исходные данные и результаты
выбирается форма хранения данных
составляются все необходимые формулы
Слайд 9Выбор метода решения.
Разработка алгоритма
анализ существующих методов решения поставленной задачи
разработка нового метода решения

(при необходимости) или определение метода решения задачи – метод преобразования исходных данных в результат
при необходимости возможен возврат к предыдущему этапы для уточнения моделей данных
Слайд 10Составление программы
преобразование алгоритма в код, написанным на языке программирования (C, C++, Java,

Python etc.)
Слайд 11Вычисление и обработка результатов
анализ полученных результатов
внесение правок в алгоритм и/или код программы
отладка

программы
Слайд 12Что такое алгоритм?
Слово «алгоритм» произошло от латинского написания имени ученого из города

Хорезма, Абдуллы (или абу Джафара) Мухаммеда бен Муса аль-Хорезми (Alhorithmi), жившего в 783 – 850 гг.
Слайд 13Что такое алгоритм?
Алгоритм – это подробное описание последовательности арифметических и логических действий,

расположенных в строгом логическом порядке и позволяющих решить конкретную задачу.
Шаг алгоритма – это каждое отдельное действие алгоритма
Алгоритмизация – составление пошагового описания процесса решения задачи.
Слайд 14Свойства алгоритмов
Определенность (детерминированность, точность) – единственность толкования правил выполнения действий и порядка

их выполнения;
Конечность – обязательность завершения каждого из действий алгоритма и алгоритма в целом;
Результативность – обязательность получения через определенное число шагов определенных результатов или сообщения о невозможности решения;
Массовость – возможность применения одного и того алгоритма для решения однотипных задач с различными исходными данными;
Дискретность – расчленение вычислительного процесса на отдельные этапы, элементарные операции.
Слайд 15Алгоритмы
Иногда также выделяют дополнительные свойства:
Эффективность
Связанность
Каждый алгоритм имеет вход и выход. Вход алгоритма

– это совокупность его исходных данных. Множество допустимых значений переменных на входе алгоритма называются областью определения алгоритма.
Выход алгоритма – это совокупность результатов его работы.
Слайд 16Пример задачи
Постановка задачи:
Разработать алгоритм нахождения наименьшего простого делителя натурального числа k, большего

единицы.
Формализация:
Входные данные: k – натуральное число, k>1;
Выходные данные: i – наименьший простой делитель числа k, i≠1.
Слайд 17Пример задачи
Метод решения:
Простым называется число, не имеющее делителей, отличных от единицы и

его самого, причем единица во множество простых чисел не входит.
Алгоритм решения задачи:
Положить целое число i равным двум и перейти на шаг 2.
Если k делится нацело на i, то завершить работу алгоритма, выдав в качестве результата i, иначе перейти на шаг 3.
Увеличить значение i на единицу и перейти на шаг 2.
Слайд 18Пример задачи
Детерминированность. Все действия определены строго и недвусмысленно.
Конечность. Величина i вначале меньше

k, ее значение увеличивается на единицу к каждому очередному выполнению шага 2, и поэтому выполнение алгоритма будет прекращено на шаге 2 при i=k, если k – простое число, или ранее при составном k.
Результативность и массовость. Этот алгоритм пригоден для нахождения наименьшего простого делителя любого натурального числа k, большего единицы.
Дискретность. Процесс разбит на отдельные этапы, возможность выполнения которых исполнителем (компьютером) не вызывает сомнений.
Слайд 19Способы представления алгоритмов
Словесный – описание алгоритмов на естественном языке;
Структурно-стилизованный способ (псевдокоды);

Графический (с помощью блок-схем);
Программный.
Слайд 20Словесное описание
Этап обработки(вычисления)
V=выражение
Где V – переменная
Проверка условия
Если условие, то идти к N
Переход

к этапу с номером N
Идти к N
Конец вычислений
Конец
Слайд 22Недостатки
отсутствует наглядность вычислительного процесса, т.к. нет достаточной формализации;
страдают многословностью записей;
допускают неоднозначность

толкования отдельных предписаний.
Слайд 23Псевдокод
Псевдокод - позволяет формально изображать логику программы, не заботясь при этом о

синтаксических особенностях конкретного языка программирования.
Обычно представляет собой смесь операторов языка программирования и естественного языка.
Является средством представления логики программы, которое можно применять вместо блок-схемы.
Слайд 24Пример
Выбираем первый элемент (i=1)
IF A>xi или xi печать сообщения и

переход на конец
ELSE переход к следующему элементу(i=i+1)
IF массив не кончился (i<=n) THEN
переход на проверку интервала
ELSE печать сообщения, что все элементы входят
в интервал
Конец
Слайд 25Графический способ
Блок-схема – это графическая интерпретация алгоритма, представляющая набор геометрических фигур, каждая

из которых изображает какую-либо операцию или действие.
Внутри фигур (блоков) кратко записывают выполняемое действие. Такую схему называют схемой программы. Схема программы – отображает последовательность операций в программе.
Слайд 26Графический способ
Формат блок-схем стандартизирован:
ГОСТ 19.701-90,
ISO 5807-85 "Схемы алгоритмов, данных, программ и

систем"
Слайд 27Графический способ
4 основных правила:
Блок-схема строится сверху вниз.
В любой блок-схеме имеется только один

элемент, соответствующий началу алгоритма, и один элемент, соответствующий концу алгоритма.
Должен быть хотя бы один путь из начала блок-схемы к любому элементу.
Должен быть хотя бы один путь от каждого элемента блок-схемы в конец блок-схемы.
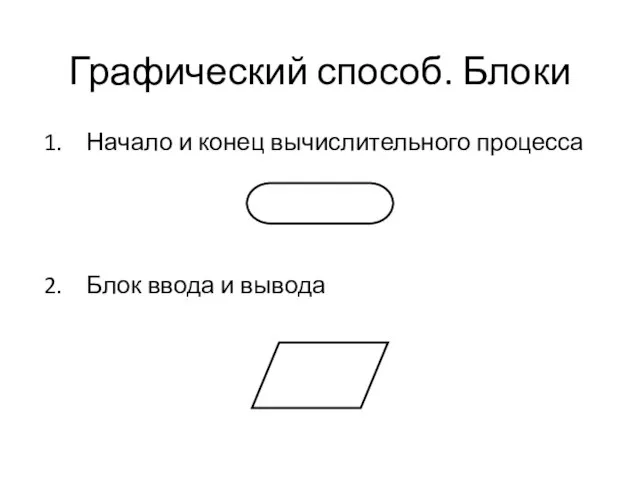
Слайд 28Графический способ. Блоки
Начало и конец вычислительного процесса
Блок ввода и вывода
Слайд 29Графический способ. Блоки
Вычислительный блок
Логический блок
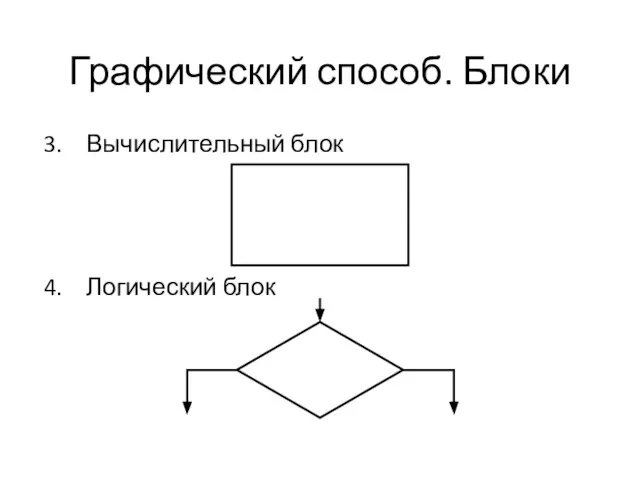
Слайд 30Графический способ. Блоки
Циклический блок
Соединитель
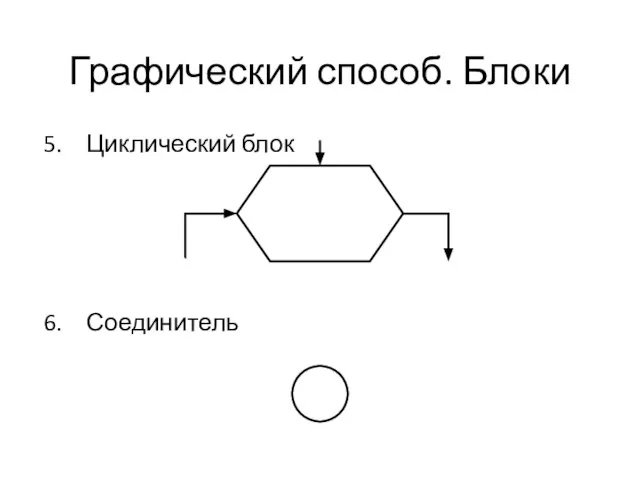
Слайд 33Основные структуры алгоритмов
Основные структуры алгоритмов – это ограниченный набор блоков и стандартных

способов их соединения для выполнения типичных последовательностей действий.
Классификация алгоритмов по структуре:
Линейный
Разветвленный (ветвление)
Циклический (повтор)
Слайд 34Виды алгоритмов
Алгоритм линейной структуры - это алгоритм, в котором направление вычислений является

единственным.
В алгоритмах с линейной структурой каждый оператор выполняется только одни раз и выполняется весь целиком, т.е. выполняются все ее операторы.
В них могут использоваться все блоки, за исключением блоков проверки условия и модификации.
Слайд 36Виды алгоритмов
Алгоритм разветвляющейся структуры - это алгоритм, в котором направление вычислений определяется

некоторыми условиями
Каждое возможное направление вычислений называется ветвью.
Каждая из ветвей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.
Структура ветвление существует в трех основных вариантах: если–то (неполная форма ветвления); если–то–иначе (полная форма ветвления); выбор.
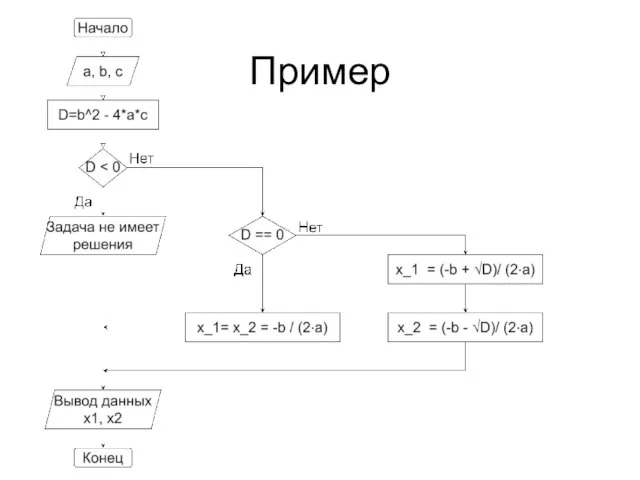
Слайд 39Пример
Вывести модуль действительного числа x.
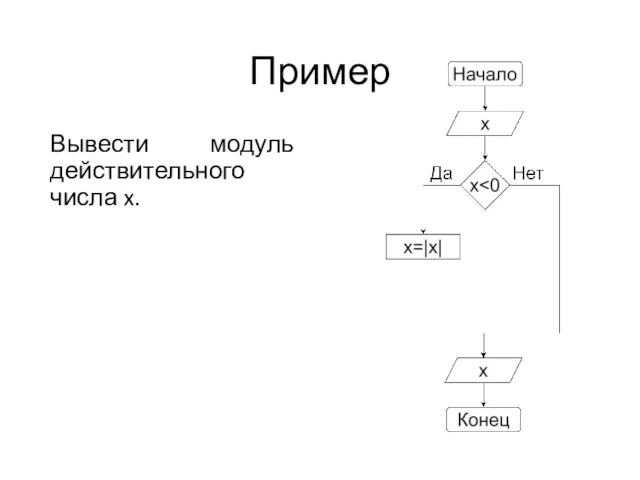
Слайд 40Виды алгоритмов
Алгоритм циклической структуры - это алгоритм, в котором отдельные участки вычислений

выполняются многократно
Циклические алгоритмы позволяют существенно сократить объем программы за счет многократного выполнения группы повторяющихся вычислений
Слайд 41Циклы: основные понятия
Цикл – совокупность действий алгоритма, связанная с повторением.
Тело цикла –

многократно повторяющиеся действия алгоритма.
Параметр цикла – величина, с изменением которой связано многократное выполнение цикла.
Условие цикла – это некоторое утверждение, которое обязательно принимает одно из значений: истина или ложь.
Слайд 42Циклы
Для организации цикла необходимо выполнить следующие действия:
Перед началом цикла задать начальные значения

параметров (переменных, используемых в логическом выражении, отвечающем за продолжение или завершение цикла;
Внутри цикла изменять переменную (или переменные), которая сменит значение логического выражения, за счет которого продолжается цикл, на противоположное;
Вычислять логическое выражение – проверять условие продолжения или окончания цикла;
Управлять циклом, т.е. переходить к его началу, если он не закончен, или выходить из цикла в противном случае.
Слайд 43Классификация циклов
Простые – циклы, не содержащие внутри себя другие циклы
Сложные - циклы,

содержащие внутри себя другие циклы
Вложенные (внутренние) – циклы, входящие в состав других циклов (цикл в цикле)
Внешние – циклы, не являющиеся составной частью других циклов, но содержащие в своем составе внутренние циклы.
Слайд 44Классификация циклов
В зависимости от месторасположения условия выполнения цикла:
циклы с предусловием (ПОКА)
циклы с

постусловием (ДО)
В соответствии с видом условия выполнения:
циклы с параметром
итерационные циклы
Слайд 45Циклическая структура «ДО»
Повторять до тех пор, пока не будет выполнено условие.
Особенность этого
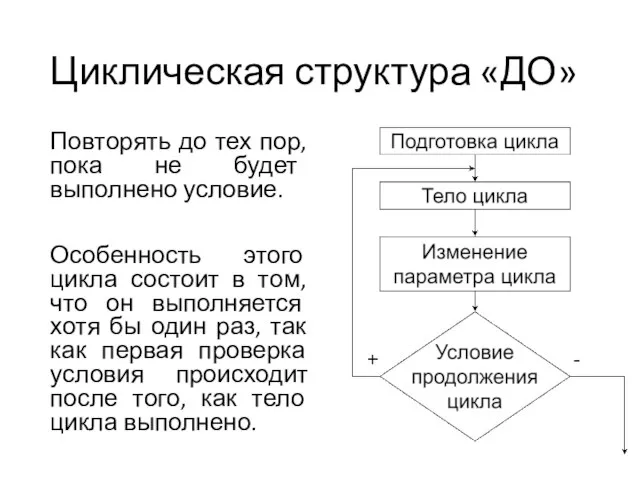
цикла состоит в том, что он выполняется хотя бы один раз, так как первая проверка условия происходит после того, как тело цикла выполнено.
Слайд 47Циклическая структура «ПОКА»
Повторять до тех пор, пока выполняется условие.
Отличается от цикла «ДО»
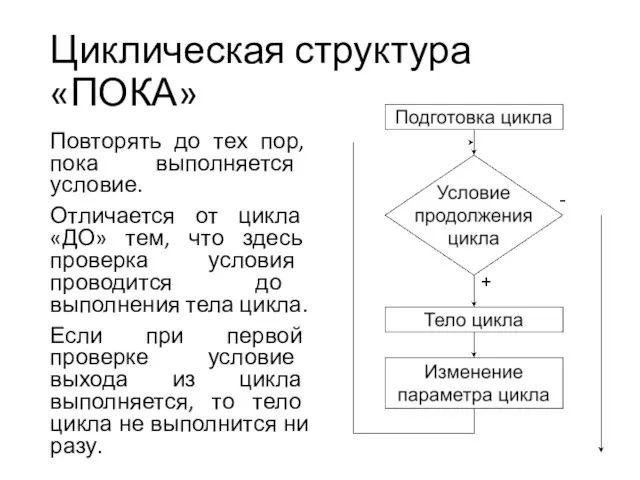
тем, что здесь проверка условия проводится до выполнения тела цикла.
Если при первой проверке условие выхода из цикла выполняется, то тело цикла не выполнится ни разу.
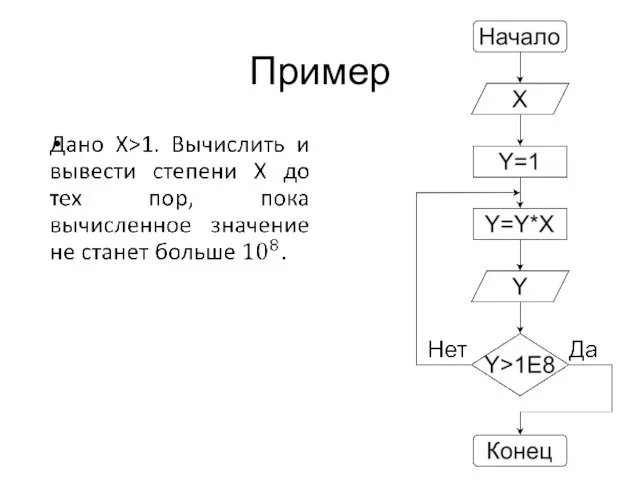
Слайд 48Пример
Дано X. Надо делить его пополам до тех пор, пока X будет
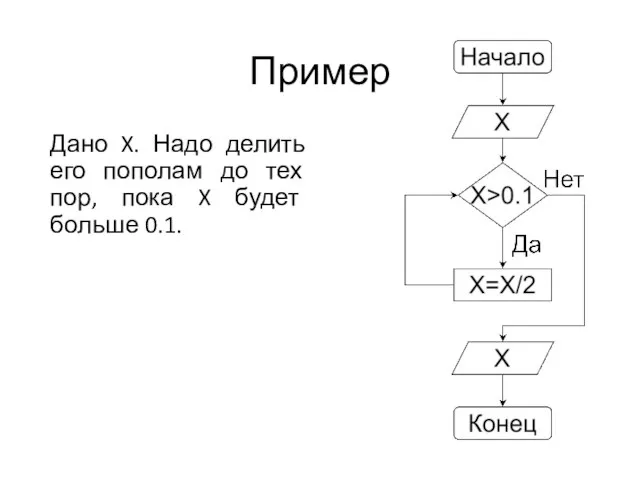
больше 0.1.
Слайд 49Циклическая структура «ДЛЯ»
В блоке «модификация» объединяются несколько блоков: подготовка цикла, проверка окончания,
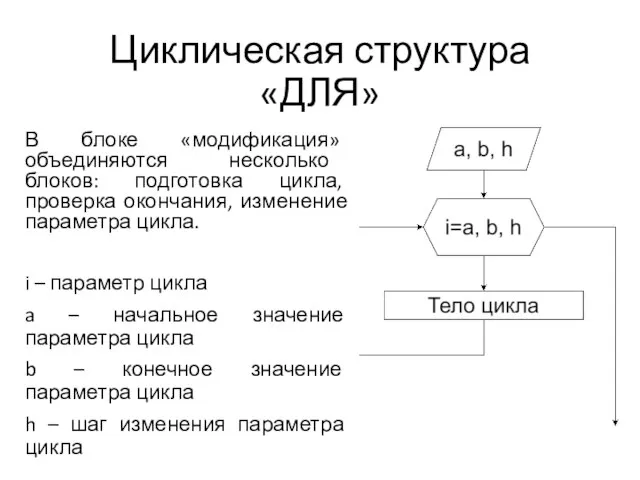
изменение параметра цикла.
i – параметр цикла
a – начальное значение параметра цикла
b – конечное значение параметра цикла
h – шаг изменения параметра цикла
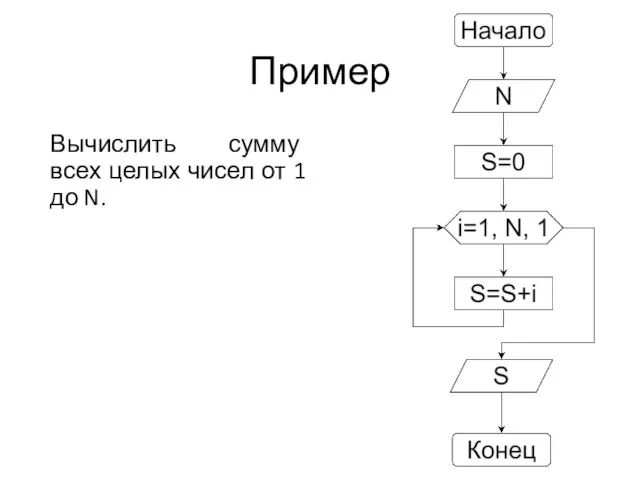
Слайд 50Пример
Вычислить сумму всех целых чисел от 1 до N.
Слайд 51Величины в алгоритмах
В алгоритмах для данных используются специальные символические обозначения, которые аналогичны

обозначениям в математике, представляют имена величин или их идентификаторы.
Типы данных: целые, вещественные, логические, текстовые (символьные) и другие.
Слайд 52Величины в алгоритмах
В алгоритмах и программах используются два вида величин:
Константа – это

величина, значение которой не изменяется в процессе выполнения алгоритма и программы.
Переменная – это величина, значение которой изменяется в процессе выполнения алгоритма и программы
Слайд 53Величины в алгоритмах
Используются простые и индексные переменные (переменные с индексом). Переменная с

индексом – это элемент некоторой заданной последовательности значений, которые называются массивом.
Массивом называется совокупность однотипных данных, связанных общим именем.
Слайд 54Величины в алгоритмах
Массив может быть одномерным (вектор), количество индексов – один; двумерным,

количество индексов – два и т.д. (матрицы).
Количество индексов определяет размерность массива.
Обращение к элементам массива: X(1), Y(2)(3).
















































 История развития вычислительной техники
История развития вычислительной техники Содержательная линия Алгоритмизации и программирования
Содержательная линия Алгоритмизации и программирования Компьютерная графика
Компьютерная графика Мультимедиа в Театральном музее
Мультимедиа в Театральном музее Управление памятью
Управление памятью Изучение лексики английского языка с помощью современных образовательных платформ
Изучение лексики английского языка с помощью современных образовательных платформ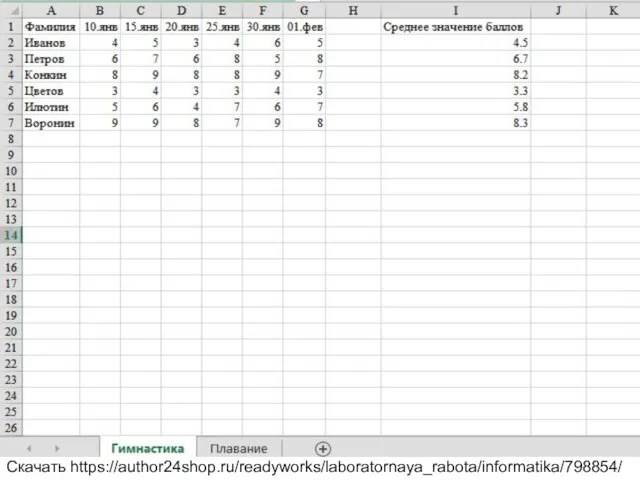 Связь между листами. Лабораторная работа
Связь между листами. Лабораторная работа Книги – ровесники нашего университета
Книги – ровесники нашего университета Работа со словарями. Библиотека Date в Python
Работа со словарями. Библиотека Date в Python Изготовление прототипов
Изготовление прототипов Проектные технологии
Проектные технологии WORD. Работа с таблицей (меню и панель инструментов)
WORD. Работа с таблицей (меню и панель инструментов) Цифровые данные
Цифровые данные Оператор выбора на языке Pascal
Оператор выбора на языке Pascal Расчетные операции в Excel Работа с датами
Расчетные операции в Excel Работа с датами Параграф 5. Представление целых чисел в компьютере
Параграф 5. Представление целых чисел в компьютере Презентация на тему Знакомство с электронными таблицами MICROSOFT EXCEL
Презентация на тему Знакомство с электронными таблицами MICROSOFT EXCEL  Всероссийская Ассоциация Блогеров
Всероссийская Ассоциация Блогеров Локальные компьютерные сети (КС). Особенности компьютерных сетей
Локальные компьютерные сети (КС). Особенности компьютерных сетей Умозаключение (4 класс)
Умозаключение (4 класс) Лекция 2
Лекция 2 ITvoice. Мобильное приложение, помогающее детям учить стихи
ITvoice. Мобильное приложение, помогающее детям учить стихи Интерактивная игра Правила безопасности в сети интернет
Интерактивная игра Правила безопасности в сети интернет Интегрированные коммуникации на примере
Интегрированные коммуникации на примере Техническая интеграция с PayOnline - методы, инструменты, вопросы и ответы
Техническая интеграция с PayOnline - методы, инструменты, вопросы и ответы Система проверки знаний учащихся на основе мобильной платформы
Система проверки знаний учащихся на основе мобильной платформы Цифровые технологии в обеспечении экономической безопасности фирмы АО Клинцовский крановый завод
Цифровые технологии в обеспечении экономической безопасности фирмы АО Клинцовский крановый завод Техника безопасности в компьютерном классе
Техника безопасности в компьютерном классе